Silva Fennica

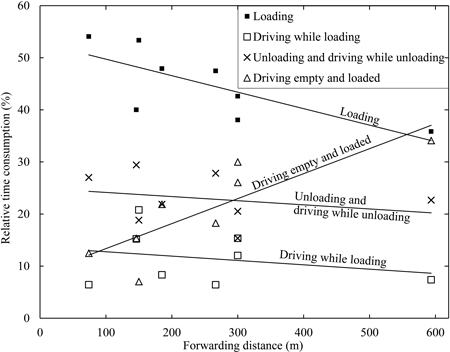
Fig. 1. The relative distribution of the forwarder’s productive machine (PM) time after fully mechanized cut-to-length (CTL) thinning operations versus forwarding distance (single way). Relationship lines are derived by regression analysis of data from Kellogg and Bettinger (1994); McNeel and Rutherford (1994); Hunt (1995); Sambo (1999); Bulley (1999); Gullberg (1995), motor-manual CTL thinning and Bruunett Mini 687F; Meek and Simard (2000), Valmet 646; Poikela and Alanne (2002), both late thinning and final felling. For the first five references, forwarding distances were calculated as the mean of driving empty and driving loaded distances.

Table 1. Data on log concentration and the number of assortments in studies of mechanized CTL, which have reported total and forwarded log concentration as well as the number assortments at harvesting site and in loads. View in new window/tab.

Table 2. Treatments included in the study (i.e. factor combinations) and their resulting levels of forwarded log concentration and distances driven between the first and the last loaded pile in a load. Each treatment was repeated three times, resulting in 24 observed loads in total.
Factors		Forwarded log concentration (m³ob (100 m)^–1)	Distance driven between the first and the last loaded pile in a load (m)
Total log concentration (m³ob (100 m)^–1)	Number of assortments in a load	Forwarded log concentration (m³ob (100 m)^–1)
6.4	1	1.3	625
	3	3.8	209
	5	6.4	125
19.2	1	3.8	209
	2	7.7	104
	3	11.5	70
32.0	1	6.4	125
32.0	3	19.2	42
m³ob (100 m)^–1 = solid m³ over bark per 100 m of the strip-road

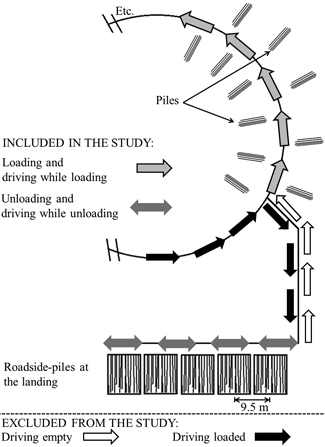
Fig. 2. The standardized circular test path defined by an imaginary log distribution. Each pile and roadside-pile contained only one of the five assortments.

Table 3. Levels of significance (p-values) and level of explained variance (R² adjusted values) obtained from the analysis of variance (ANOVA) of the main effects on the work elements’ time consumption and on the loading and unloading components. α is the number of assortments in a load, β is total log concentration on the strip-road and (αβ) is the fixed interaction effect.
Dependent variable	p-value			R² (adj) (%)	Number of observations (n)
Dependent variable	α	β	(αβ)	R² (adj) (%)	Number of observations (n)
Time consumption for work elements (PMmin (m³ob)^–1)
Work elements pooled	0.006	<0.001	<0.001	89.8	18
Loading	<0.001	0.393	0.985	63.5	18
Driving while loading	<0.001	<0.001	<0.001	99.8	18
Unloading	<0.001	0.629	0.596	81.9	18
Driving while unloading	<0.001	0.538	0.538	88.6	18
Loading components
Time consumption for a loading stop (PMmin)	<0.001	<0.001	<0.001	67.5	378
Time consumption for distance driven between the first and the last loaded pile in a load (PMmin m^–1)	0.182	0.132	0.074	32.9	18
Time consumption for a loading crane cycle (PMmin)	<0.001	0.076	0.721	11.5	526
Number of loading stops per load	<0.001	<0.001	<0.001	96.9	18
Number of loaded piles per stop	<0.001	<0.001	<0.001	69.2	378
Number of crane cycles per loading stop	<0.001	<0.001	<0.001	73.0	378
Number of loaded piles per crane cycle	0.054	<0.001	0.028	6.9	526
Unloading components
Time consumption for an unloading stop (PMmin)	0.016	0.917	0.878	5.0	52
Time consumption for an unloading crane cycle (PMmin)	<0.001	0.767	0.470	15.1	200
Number of unloading stops per load	<0.001	0.344	0.344	94.8	18
Number of unloading crane cycles per load	<0.001	0.926	0.168	85.3	18
Number of unloading crane cycles per stop	<0.001	0.659	0.735	71.6	52
Significant values (p < 0.05) in bold.

Table 4. Time consumption (mean and standard deviation (SD), PMmin (m³ob)^–1) for work elements by total log concentration and the number of assortments in a load.
Work element	Total log concentration (m³ob (100 m)^–1)	Number of assortments in a load
		Balanced two-way ANOVA				Supplements for one-way ANOVA
		1		3		2		5
		Mean	SD	Mean	SD	Mean	SD	Mean	SD
Work elements pooled	6.4	3.19^A,a	0.17	2.90^A,b	0.02			3.60^c	0.09
	19.2	1.97^BC,a	0.06	2.38^B,a	0.33	1.95^a	0.13
	32.0	1.69^C	0.11	2.39^B	0.16
Loading	No effect	0.94^a	0.08	1.13^b	0.06	1.04^ab	0.01	1.40^c	0.10
Driving while loading	6.4	1.86^A,a	0.05	0.72^B,b	0.02			0.46^c	0.03
	19.2	0.72^B,a	0.01	0.26^D,b	0.02	0.36^c	0.01
	32.0	0.41^C	0.03	0.13^E	0.01
Unloading	No effect	0.34^a	0.03	0.89^b	0.17	0.47^a	0.07	1.43^c	0.20
Driving while unloading	No effect	0^a	0	0.16^b	0.04	0.07^ab	0.05	0.31^c	0.11
Different superscript uppercase letters within work elements pooled and driving while loading indicate significant differences (p < 0.05) between the six combinations of total log concentration and 1 and 3 assortments (Two-way ANOVA with Tukey test). When there was no effect from total log concentration (see Table 3), data within 1 and 3 assortments were pooled (i.e. means based on 9 loads instead of 3). Different superscript lowercase letters within rows indicate significant differences (p < 0.05) (One-way ANOVA with Tukey test).

Table 5. Observations (mean and SD) for loading components by total log concentration and the number of assortments in a load. View in new window/tab.

Table 6. Comparisons at equal forwarded log concentrations: the main effect of number of assortments in a load α and the covariate forwarded log concentration on the strip-road γ (m³ob (100 m)^–1). View in new window/tab.

Table 7. Observations (mean and SD) for unloading components by the number of assortments in a load. View in new window/tab.

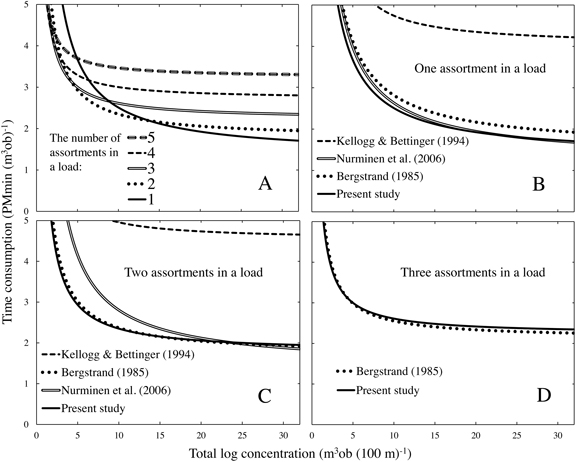
Fig. 3. Panel A: total time consumption in this study for the work elements loading, driving while loading, unloading and driving while unloading. Panels B–D: the total time consumption in this study compared with published studies for 1, 2 and 3 assortment loads. Driving while loading velocity 38.5 m min^–1 was used in models by Bergstrand (1985) and Nurminen et al. (2006). The model for 2 saw log assortments was taken from Nurminen et al. (2006). The load-size 8 m³ob was used in the model created by Kellogg and Bettinger (1994). The pile-size 0.26 m³ob and the model for a large-sized forwarder were taken from Bergstrand (1985), with the proportion of difficult piles set as null. In each panel (A–D), the total number of assortments at a harvesting site is five.

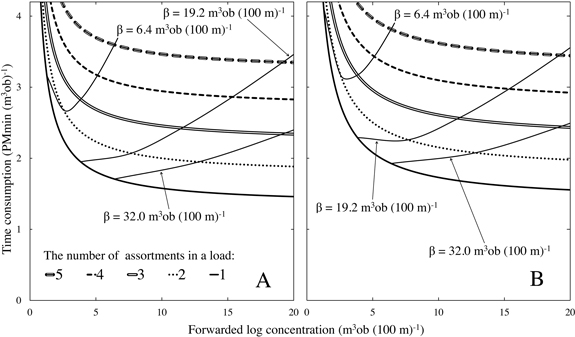
Fig. 4. Total time consumption for loading, driving while loading, unloading and driving while unloading as a function of forwarded log concentration m³ob (100 m)^–1 and dependent on the number of assortments in a load (i.e. load type). Additional curves (β) indicate the total time consumption as functions of total log concentrations applied in this study. Data in panel A is based directly on the models presented in the result section. In panel B, the time consumption for driving while loading is increased by 50% to simulate 33.3% slower mean velocity. β curves are based on the assumption that five equally large assortments constitute the total log concentration. Increasing number of equally large assortments at a harvesting site would move β curves to the left, while decreasing their number would have the opposite effect.