Table 1. The fixed-effects ingrowth model for Scots pine estimated with the zeroinfl function in R package pscl. The function estimates the dispersion parameter in form log(1/α). G is the stand basal area, VT and CT are the indicator variables for sub-xeric and xeric or poorer forest types. Log(T) and log(A) are used as offsets, where A = 100 m2 is the area of plot and T = 5 yrs is the length of the growth period.
Predictor Estimate Std. Error Pr(>|z|)
Count model (negative binomial with log link)
log(T) 1
log(A) 1
Intercept –6.82 0.41 <2e–16
Gpine –0.131 0.112 0.023
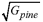0.783 0.308 0.011
VT 0.633 0.250 0.011
CT 1.64 0.34 1.2e–06
ln(1/α) –1.16 0.209
Zero-inflation model coefficients (binomial with logit link)
Intercept –13.6 3.5 0.0001
ln(Gpine + 0.01) –0.307 0.083 0.00021
√G 6.1 1.5 5.9E–05
G –0.58 0.16 0.0003
VT –1.21 0.36 0.00075
α = 3.19; Log-likelihood –905.2 on 11 degrees of freedom.
Table 2. The fixed-effects ingrowth model for Norway spruce. OMT is an indicator variable for herb-rich or better site. TS is the temperature sum. The other symbols are as in Table 1.
Predictor Estimate Std. Error Pr(>|z|)
Count model (negative binomial with log link)
log(T) 1
log(A) 1
Intercept –6.61 0.54 <2e–16
log(Gspruce + 0.01) 0.148 0.029 2.9e–07
max(Gspruce – 13.0) –0.0207 0.0109 0.056
TS 0.00126 0.00048 0.0082
log(1/α) –0.83 0.11
Zero-inflation model coefficients (binomial with logit link)
Intercept –1.75 0.46 8.6e–05
log(Gspruce + 0.01) –0.359 0.073 9.0e–07
OMT 1.12 0.43 0.0085
CT 1.10 0.48 0.021
α = 2.28; Log-likelihood –22987 on 9 degrees of freedom.
Table 3. The fixed-effects ingrowth model for birch (combined ingrowth of silver and downy birch). The symbols are as in Table 1.
Predictor Estimate Std. Error Pr(>|z|)
Count model (negative binomial with log link)
log(T) 1
log(A) 1
Intercept –3.15 0.18 <2e–16
Gpine 0.0923 0.0090 <2e–16
Gbirch –0.109 0.045 0.016
√Gbirch 0.349 0.150 0.020
G –0.113 0.0091 <2e–16
VT –0.50 0.16 0.0016
CT –0.87 0.29 0.0032
log(1/α) –1.013 0.092
Zero-inflation model (binomial with logit link)
Intercept –6.40 1.57 0.000044
log(Gbirch + 0.01) –0.565 0.17 0.00078
G 0.142 0.033 0.000014
VT 0.822 0.51 0.11
CT 2.41 0.75 0.0014
α = 2.57; Log-likelihood –2700 on 13 degrees of freedom.
Table 4. Statistics for the fixed-effects ingrowth models. Row “P(Residual > 0)” gives the proportion of positive residuals.
Variable Minimum Maximum Mean sd
Scots pine
Ingrowth 0 68 0.90 4.07
Censored ingrowth 0 5 0.457 1.26
Probability of extra zeroes (p) 0.0009 0.97 0.68 0.28
Prediction 0.018 8.10 0.890 1.38
Residual –8.10 64.34 –0.0016 3.89
P(Residual > 0) 0.11
Pearson residual –0.55 28.79 –0.0020 1.13
Censored prediction 0.017 2.39 0.47 0.52
Censored residual –2.37 4.90 –0.001 1.15
Censored Pearson residual –1.05 9.91 –0.007 0.93
Norway spruce
Ingrowth 0 47 2.61 5.3
Censored ingrowth 0 5 1.47 1.95
Probability of extra zeroes (p) 0.04 0.74 0.22 0.20
Prediction 0.27 5.0 2.60 1.29
Residual –4.84 43.6 0.010 5.16
P(Residual > 0) 0.27
Pearson residual –0.61 12.97 0.0010 1.08
Censored prediction 0.24 2.27 1.49 0.59
Censored residual –2.25 4.71 –0.022 1.84
Censored Pearson residual –1.04 4.97 –0.014 0.98
Birch (silver birch and downy birch)
Ingrowth 0 120 5.45 12.8
Censored ingrowth 0 5 1.77 2.14
Probability of extra zeroes (p) 0.0015 0.940 0.17 0.21
Prediction 0.035 23.4 5.33 4.29
Residual –19.4 102.7 0.12 11.7
P(Residual > 0) 0.25
Pearson residual –0.60 11.4 –0.0023 1.02
Censored prediction 0.035 3.31 1.75 0.80
Censored residual –3.19 4.48 0.023 1.95
Censored Pearson residual –1.47 6.03 0.0098 1.00
1

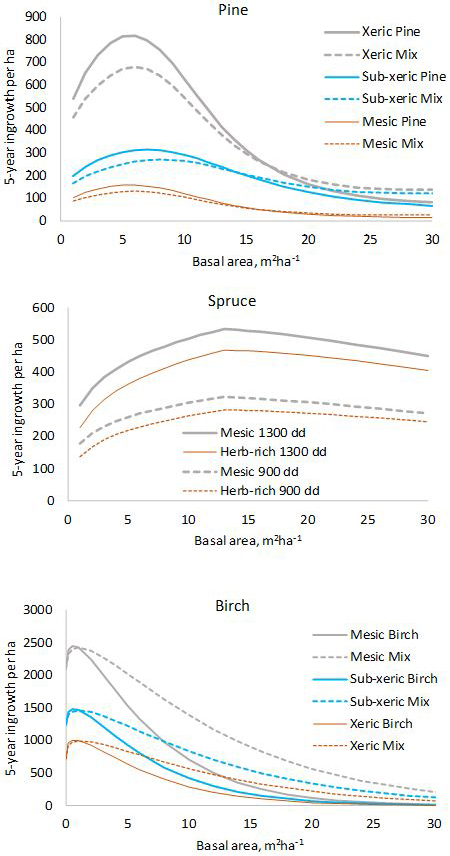
Fig. 1. Five-year predictions calculated with the fixed-effects model shown in Tables 1–3. log(10000) and log(5) were used as offsets to obtain per-hectare values for five years. In the diagram for pine, “Mix” refers to a stand where 50% of the basal area is pine and 50% is other species. In the diagram for birch, “Mix” is a stand where 50% of the basal area is birch and 50% is pine.

Table 5. The mixed-effects ingrowth model for Scots pine. VT is the sub-xeric type, and CT is the xeric type.
Predictor Estimate Std. Error Pr(>|z|)
Conditional model
log(T) 1
log(A) 1
Intercept –6.47 0.56 <2e–16
ln(Gpine + 0.01) 0.323 0.074 1.4E–05
√G –1.04 0.13 6.4E–15
VT 0.73 0.23 0.0018
CT 1.23 0.37 0.00082
Zero-inflation model
Intercept –5.40 0.88 8.6e–10
α = 0.135; σ = 3.06; Log-likelihood = –820.6 on 7 Df.
Table 6. The mixed-effects ingrowth model for Norway spruce. TS is the temperature sum and CT is the xeric type.
Predictor Estimate Std. Error Pr(>|z|)
Count model
log(T) 1
log(A) 1
Intercept –7.58 0.69 <2e–16
ln(Gspruce + 0.01) 0.287 0.032 <2e–16
max(Gspruce – 13.0) –0.0532 0.0126 2.4e–05
LS 0.000716 0.00060 0.235
Zero-inflation model
Intercept –3.74 0.27 <2e–16
ln(Gspruce + 0.01) –0.32 0.12 0.0096
CT 1.31 1.02 0.20
α = 0.0071; σ = 1.79; Log-likelihood = –2156.2.
Table 7. The mixed-effects ingrowth model for birch.
Predictor Estimate Std. Error Pr(>|z|)
Conditional model
log(T) 1
log(A) 1
Intercept –4.27 0.20 <2e–16
G –0.127 0.010 <2e–16
log(Gbirch + 0.01) 0.221 0.030 1.6e–13
Gpine 0.0815 0.0107 2.7e–14
CT –0.21 0.19 0.26
Zero-inflation model
Intercept –5.03 0.86 4.2e–09
G 0.0929 0.033 0.004
α = 0.101; σ = 2.056; Log-likelihood = –2615.2.
Table 8. Statistics for the mixed-effects ingrowth models. Notations (11) and (12) refer to Eqs. 11 and 12, respectively.
Variable min max mean sd
Scots pine
Probability of extra zeroes (p) 0.0045 0.0045 0.0045 0
Prediction 0.0001 0.767 0.039 0.072
Prediction 0.010 82.91 4.21 7.84
Residual (11) –0.6668 67.87 0.8567 4.05
P(Residual (11) > 0) 0.16
Residual (12) –72.12 54.48 –3.318 7.60
P(Residual(12) > 0) 0.055
Pearson residual (11) –8.01E–05 0.260 0.002 0.012
Pearson residual (12) –0.0087 0.252 –0.007 0.012
Censored prediction 0.0075 1.86 0.390 0.335
Censored residual –1.80 4.83 0.068 1.17
Censored Pearson residual –0.84 6.80 0.019 0.94
Norway spruce
Probability of extra zeroes (p) 0.0068 0.277 0.042 0.060
Prediction 0.090 1.37 0.695 0.382
Prediction 0.45 6.83 3.47 1.90
Residual (11) –1.30 46.27 1.91 5.25
P(Residual(11) > 0) 0.43
Residual (12) –6.47 43.37 –0.86 5.20
P(Residual(12) > 0) 0.24
Pearson residual (11) –0.040 6.560 0.12 0.39
Pearson residual (12) –0.20 6.41 –0.038 0.39
Censored prediction 0.33 2.07 1.34 0.54
Censored residual –2.02 4.64 0.13 1.85
Censored Pearson residual –0.99 4.81 0.070 1.07
Birch (silver birch and downy birch)
Probability of extra zeroes (p) 0.0074 0.45 0.055 0.050
Prediction (11) 0.0070 5.50 1.18 1.09
Prediction (12) 0.058 45.5 9.79 9.00
Residual (11) –5.23 117.2 4.27 12.4
P(Residual(11) > 0) 0.43
Residual (12) –43.3 96.7 –4.35 12.9
P(Residual(12) > 0) 0.18
Pearson residual (11) –0.014 2.30 0.057 0.17
Pearson residual (12) –0.12 2.20 –0.041 0.17
Censored prediction 0.052 3.27 1.63 0.75
Censored residual –3.22 4.57 0.142 1.98
Censored Pearson residual –1.55 4.81 0.080 1.07
2

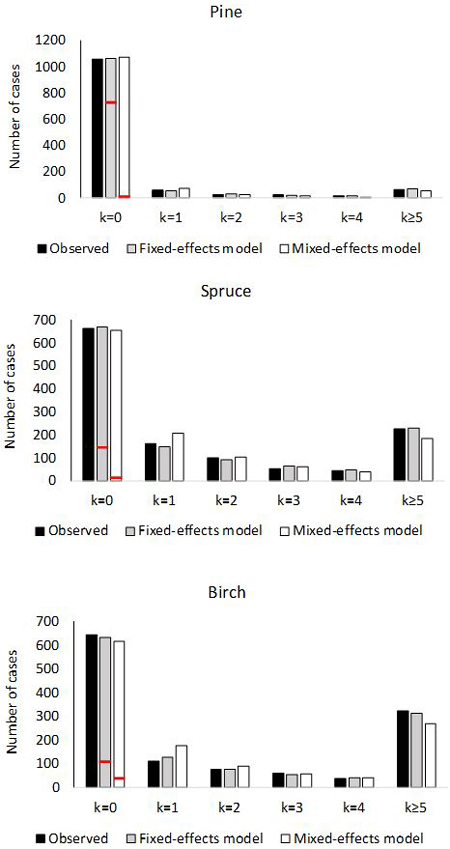
Fig. 2. Number of plots with 0, 1, 2, 3, 4 or ≥5 ingrowth trees based on observed and predictedingrowth. The marginal distribution of the predicted ingrowth is computed using Eq. 1. The frequency of extra zeros is shown with the red horizontal line.

3

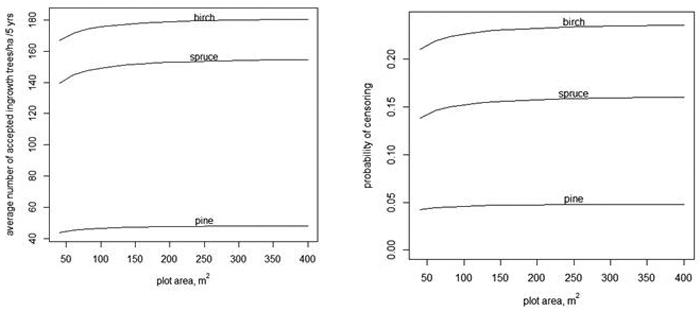
Fig. 3. The average number of accepted ingrowth trees per ha when the censoring limit is 500 trees per ha, i.e., the censored variable is min(y,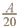A/20) (left) and the average probablity that some ingrowth trees within a plot are censored when 500 trees/ha are accepted (right).

4

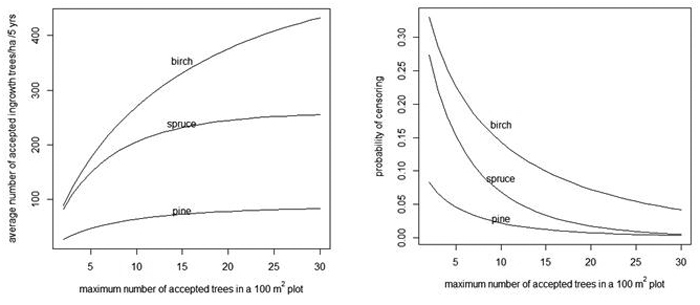
Fig. 4. Average number of acceptable ingrowth trees/ha in 5 years (left) and the probability that some trees are censored in a 100 m2 plot (right) as a function of the maximum number of acceptable trees in a 100 m2 plot. As a reference, note that without censoring there are 90, 259 and 524 trees/ha for pine, spruce and birch, respectively (see the "Prediction" rows of Table 4).