The box assignment problem in log yards
Rathke J., Huka M. A., Gronalt M. (2013). The box assignment problem in log yards. Silva Fennica vol. 47 no. 3 article id 1006. https://doi.org/10.14214/sf.1006
Highlights
- Logistic approach for the optimization of log yard in terms of arrangement of storage boxes and ejection boxes reduced transportation time by 16 percent compared with the original solution.
Abstract
This paper presents an optimization approach to minimizing log yard round wood transportation time for a medium sized hardwood sawmill. The log yard, which has to ensure a smooth raw material supply to the entire production process, is the first processing step in a sawmill. The log yard also serves as an internal round wood sorting and storing capacity. Thus, an optimal assignment of ejection boxes, storage boxes and feeding carriages is required to minimize transportation time at a log yard. The main contribution of this paper is to present an integrated approach which simultaneously takes into account log transportation time, storage capacity and yard crane deployment. The approach is based on two steps: a) defining storage spaces per batch and calculating distances and b) determining optimum box assignments in the log yard in order to minimize overall transportation distance. The solution in step b) is compared with the results obtained by random box assignment as well as a spreadsheet based planning method. We have been able to show that our approach is much more flexible and results are more than 16 percent better than the corresponding real life solution.
Keywords
log yard planning;
sawmill;
linear optimization
- Rathke, University of Natural Resources and Life Sciences, Institute of Production and Logistics, Feistmantelstraße 4, 1180 Vienna, Austria E-mail joern.rathke@boku.ac.at
-
Huka,
University of Natural Resources and Life Sciences, Institute of Production and Logistics, Feistmantelstraße 4, 1180 Vienna, Austria
E-mail
maria.huka@boku.ac.at

- Gronalt, University of Natural Resources and Life Sciences, Institute of Production and Logistics, Feistmantelstraße 4, 1180 Vienna, Austria E-mail manfred.gronalt@boku.ac.at
Received 30 November 2012 Accepted 4 July 2013 Published 4 October 2013
Views 73568
Available at https://doi.org/10.14214/sf.1006 | Download PDF

1 Introduction
The log yard offers the possibility of sorting and storing round wood before being processed on the saw line. The log sorting process is performed on a sorting chain conveyor which ejects the logs into ejection boxes depending on length, diameter and quality. Ejection boxes are comparably small as the only purpose is to store a couple of logs before they are transported to storage boxes. Storage boxes are capable of storing raw material for the batch wise material supply of the saw line. This paper deals with the arising box assignment problem in log yards in order to minimize overall transportation distance from ejection boxes to storage boxes and afterwards to the saw line. Usually, it is a loader or crane that realizes these transports. Although the box assignment problem in log yards is daily routine and not new, we do not know any paper which presents the formal problem and proposes a solution approach. The data used throughout the paper and the description is provided by a hardwood sawmill with an annual production capacity of 30 000 cubic meters. One of the main characteristics of this sawmill is that it produces hardwood and softwood with a distribution of 95 percent hardwood and 5 percent softwood. Research for improving sawmill’s productivity mainly focuses on cutting pattern generation (see Todoroki and Rönnqvist (2002), Yanasse and Limeira (2006)). However, in order to improve operating efficiency additional material flow considerations are required. Simulation has some tradition to optimize processes in the forest products industry. Mendoza et al. (1991) present one of the earliest papers dealing with the topic of hardwood sawmill optimization and Randhawa et al. (1994) show the topic of object orientation for sawmill simulation. Dogan et al. (1997) applied simulation in a hardwood sawmill to model the sawmill operations, while Kyle and Ludka (2000) used simulation for the optimization of a furniture manufacturer. Baesler et al. (2002) and Baesler et al. (2004) provide information concerning simulation and artificial intelligence techniques for improvements in wood industry productivity.
Greigeritsch et al. (2007) focus on short term production planning and discrete event material flow simulation using simulation for finding the system bottleneck and planning tasks for scheduling an optimized production whereas Gronalt and Greigeritsch (2008) present an analyzing tool for supporting saw milling industries by using a detailed material flow evaluation and computer simulation techniques. Greigeritsch (2009) determined production planning processes for softwood sawmills including the optimization of the sorting line of the saw line and the reservation planning of dry kilns. Ramis et al. (2004) identified bottlenecks at a sawmill using simulation, while Adams (1984) used DESIM to simulate and design hardwood sawmill systems. The DESIM system allows simulation of material routing and simulations of complete sawmill processes, including downtime analysis and profitability, which makes it too clumsy for the daily usage of log yard storage optimization. Hence, no direct applicable solution for planning and optimization the log yard could be found in literature.
A comparable approach in the domain of a slab yard is presented by Dohn and Clausen (2010). Here, the material flow, including transportation, storage and demand, was simulated by means of a heuristic model. As only the log yard has to be optimized in this approach, the heuristic method with a precise definition of the restrictions turns out to be the system of choice. Hirsch et al. (2012) present a crane scheduling approach to improve the material handling in a roof tile production system.
The objective of this paper is to provide a solution approach to the box assignment problem in log yards. The former way of assortment allocation worked on an ad hoc basis. The storage boxes were filled, depending on whether they were empty or not, and transportation time was not considered. In the Excel-based real world decision rules, the heuristic model and the optimization models the first three ejector boxes were blocked for oversize, undersize and metal containing logs. The paper is structured as follows: First, an overview of the entire process of round wood handling is given. Next, system data (i.e. assortment volume, box size, transportation capacity and volume as well as the consumption rate per shift) are described and the calculation approach is presented. It is separated into three different steps. First, an Excel based easy to handle heuristic was coded for comparison with best practice. Second, we formulate some variances of an optimization model to generate a baseline for improvements. The double-stage approach solves the problem stepwise, while the partition model optimizes the whole system. Third, for further improvements, the calculations were done allowing the multiple box assignment to one ejector box (partition model). Finally, this systematic of multiple box assignment was applied to the originally shaped log yard layout. All calculations were compared by using real life data.
2 Material and methods
2.1 Process description
In a sawmill logs are sawn into boards with different thicknesses during the initial production process (see e.g. Fronius (1991) and Wagenführ and Scholz (2008)). During the production the characteristics of a log have an effect on processing times, quality and yield of the produced boards. In general, these log parameters can be defined by species, grade and scale. Grade is the determination of the log quality which reflects the estimated yield of the lumber, while scale means the volume of a log which is measured in cubic meters. The log yard serves as storage where logs are stored according to their length, diameter and quality.
The analyzed sawmill processes three hardwood species: beech (Fagus sylvatica), European oak (Querqus robur/Querqus patrea), European Ash (Fraxinus excelsior) and a small amount of softwood. As beech production accounts for approx. 75 percent of the total annual production, the log yard will be oriented for this raw material segment. Therefore, the assortment arrangement changes 3 to 8 times per year while the changes mainly depend on species and changes to length.
Assortment in terms of wood processing includes specific details of one batch as for instance length, quality and diameter. Prior to the sawing process, logs are measured, cut to length, sorted and stored on the log yard. The material flow and the used transportation equipment of the log yard are shown in Fig. 1. While the boxes represent the process, the arrows represent the material flow. The encircled boxes show those processes which are especially regarded. The material transportation between the boxes that are not encircled is performed by conveyor bands or rolls with continuous movement. Clearly, the production rate at the sawmill must cope with the feeding rate of the logs and the yard crane productivity.
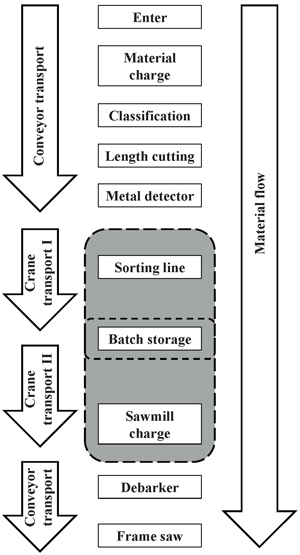
Fig. 1. Material and process flow in log yard.
Fig. 2 shows a typical log yard layout and the log’s flow. The layout has been used as a starting point for our calculations. Before being placed on the conveyor system {1} the logs are sorted by species and subsequently they are pre-stored. In the system the logs are first two dimensional measured by means of an opto-electronic measurement device. The combination of log shape and human quality grading identifies the optimum cut in length {2} which ranges in this case from 3.5 to 6 m in 0.5 m steps. The metal detector {3} analyzes metallic enclosures when the log passes through its electric field. If metal is found, the field shifts, which can be measured. The position of the metal is marked by color and the log is ejected. Having passed the metal detector, the log is ejected according to diameter and length {4}. The sorting line consists of a chain conveyor with mechanical ejectors, putting the logs into one of eighteen ejection boxes.
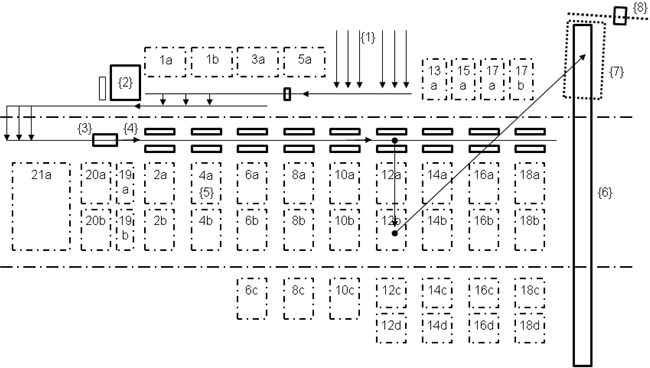
Fig. 2. Original shaped log yard.
If a certain box {5} is full, a gantry crane {6} transports the logs into one of the assortment storing boxes. The crane moves with a speed of 80 m/min (crane) and 100 m/min (orthogonal trolley traveling) respectively. The ultimate load of the crane is at 8 tonnes according to machinery data. As the claw has a weight of 0.7 tonnes, the effective bearing load is at 7.3 tonnes. The capacity of transportation depends on the relative density of the beech logs, yielding about 1.0 tonnes per cubic meters in moist condition.
Assuming this the log diameter and the log weight restrict the transportation capacity. The gantry crane is depending on the number of transportation moves, a smaller or bigger bottleneck on the log yard. As the material flow on the conveyor system is fixed the only possibility to improve the productivity of the crane is to minimize the total transportation time and to set it as the objective function. In contrast to that the storing box capacity depends mainly on the log diameter. In current status, storage boxes are designed to cover a high variability of assortments. When one assortment is finished the logs are transported to the sawmill charging {7}. Straight before the sawing process logs are debarked. The debarking process {8} directly before the sawing process offers a natural protection layer. Even more this process chain permits the distribution of clean logs to the saw as all contamination is removed in combination with the bark. The level of a finished assortment is determined first visually depending on the filling degree of the storage box and second in correspondence with the gathered measurement data of the volume determination. In this case the sawing process is done by means of a frame saw. The limiting factors of this saw milling technology are the maximum width which can pass the frame, meaning the maximum log diameter. Other effects are the downtime if the sawing pattern has to be changed and the consumed energy which depends on the number of saws clamped in the frame.
2.2 Overall approach
The objective of this study is to optimize the log yard performance by reducing the overall average transportation distances and time by box assignment decisions. Basic data required or calculated are: feeding volume, assortment size per diameter and quality, volume size of storage boxes, distances from ejection boxes to storage boxes and saw charge for a given yard layout. At first the feeding amount per time period is required. Following on this the assortment volume per shift is determined. Subject on this value the storage volume and the needed space are calculated and adapted respectively. The approach of this study was to develop both an easy to handle spreadsheet approach and to compare its result with the solution of optimization models. This task was restricted by the box arrangement and size on the yard, transportation capacity and even more the material demand of the production. The resulting planning problem to obtain the assignment and related material flows for a log yard is formulated as a binary integer problem.
During the first stage of the double-stage model we assign every assortment to a storage box in order to minimize the corresponding transportation time from storage box to the material charge. The next stage is to optimize the assignment for every assortment to an ejection box, given the results of the first stage.
More advanced the problem is solved with the partition approach which is described later. After due consideration it occurred that when looking at the whole assignment at once a better solution could be gained. Furthermore, the fragmentation of the assortment into several storage boxes is permitted in this model. When solving the problem the solution can be improved compared to the double-stage approach. But the computational efforts are much higher which restricts its use for large problem instances.
Feeding volume
Essential for the calculation of the feeding volume are the diameter and the length of the transported raw material. For the calculation of this value the two dimensional volume determination of the mill entry control was used. Following on the data quality control, the found values were sorted by diameter classes of the log. The classes were separated in 5 cm steps as most of the investigated production data used a variation of the log diameter of 5 cm. The frame-saw works with a constant feeding speed, within one assortment. This is due to continuing placement of the next log before the machine, while the nearly processed log is in its end phase of sawing. Assuming this, the length of the log has no effect on the speed of the frame saw.
Determination of the storing size
The storage size for one assortment was determined using the equations given by Fronius (1989). The logs are stored in storage places with a variable width and a height of 4.5 m. Even more a filling factor is added as depending on shape and straightness of the logs the boxes include a certain amount of unused space. In our case a filling factor of 0.8 was used. The boxes are filled after the end of the stands in a trapezium shaped manner. The top load allows a higher storage volume of 15 percent in average, determined over all assortment dimensions. In order to compare what assortments fit into which specific boxes the shift demand was divided by the filling factor 0.8 yielding the minimum box volume.
Box size adoption
The box size adoption was mainly performed by enlarging the storage size (boxes 13a and 15a) as well as pooling neighboring boxes (for instance 12a+b and 12c+d see Fig. 2). A comparison of the original box width with the assortment volume that is needed to operate the mill for one shift shows that only fifty percent of the batches can be stored in one single box. This led to a reorganization of the log yard with a reduction from the original 42 storing boxes to a number of 28.
2.3 Model formulation
The box assignment problem is formulated below as a binary integer problem. The following notation is used to specify the mathematical model.
Indices
A Set of assortments (a = 1, ..., 15)
E Set of ejection boxes (e = 1, ..., 18)
S Set of storage boxes (s = 1, ..., 28/42)
Parameter
Na Number of trips per assortment a, due to the diameter of the assortment and the demand per set assortment
TMs Transportation time from storage box s to the material charge
TSes Transportation time from ejection box e to storage box s
TTes Total transportation time for every assortment from ejection box e to storage box s and to the material charge
Cs Capacity of storage box s
Va Maximal volume of assortment a
Variables
xas 1 if assortment a is assigned to storage box s, 0 otherwise
yae 1 if assortment a is assigned to ejection box e, 0 otherwise
wes 1 if storage box s is filled with material from ejection box e, 0 otherwise
vaes Filling factor of assortment a in ejection box e and storage box s
Two objective functions (i.e. double-stage and partition) are used to minimize the transportation time.
Double-stage model
First the double-stage method is analyzed, where the assignments are solved sequentially. Beforehand a matrix showing the transportation time of each traveling route offers the locking of ejector boxes. This is related to the problem of defect or reserved ejector boxes and stock boxes. This matrix provides input data for further calculation steps. The optimization system is described as follows:
Stage 1

The objective function (1) minimizes the transportation time from storage box s to the material charge, taking into account the numbers of trips per assortment a. The first constraints (2) ensure that the available storage volume is not exceeded by the assortment. Under the very restrictive assumption that every assortment fits into even the smallest storage box without having to divide it, these constraints are redundant. The constraints (3) guarantee that every assortment is assigned to exactly one ejection box. Whereas the next constraints (4) make sure that not more than one assortment can be placed in one ejection box and not every ejection box has to be used. The last constraints (5) define the binary decision variables.
Stage 2
With the result of stage 1 the next instance is going to be solved. Therefore, the best assignment of assortment a to ejection box e is calculated.

Again, the objective function (6) minimizes the transportation time from ejection box e to storage box s taking into account the optimal assignment of assortment a to storage box s, xas from stage 1. Constraints (7) and (8) make sure that the assignment of assortment to ejection box is performed correctly. The last constraint (9) is the binary constraint.
Partition model
For simplification the number of boxes has been reduced and therefore the fragmentation of an assortment is not allowed in the previous shown double-stage model. As an expansion the solution of a model where the assortment can be divided into several storage boxes was investigated.
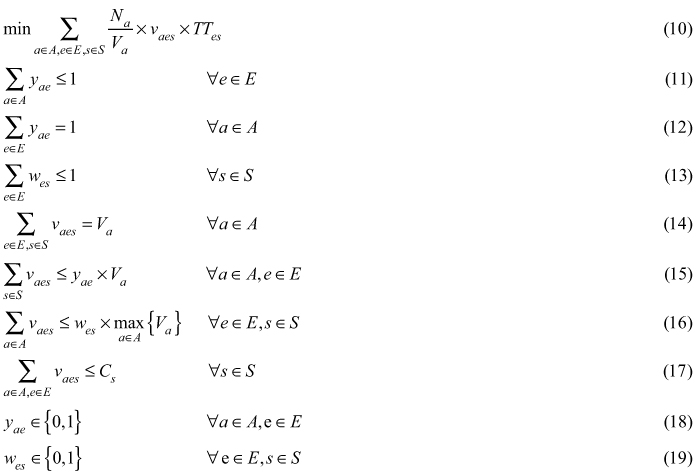
Objective function (10) minimizes the total transportation time. Constraints (11) and (12) guarantee the right assignment of every assortment a to exactly one ejection box e. Whereas constraints (13) ensure that each storage box s is used at most one time. The next two constraints (14) and (15) make sure that the whole volume of every assortment a is assigned to exactly one ejection box e. Whilst constraints (16) manage the filling over all assortments a into storage boxes s and ejection boxes e. The filling cannot exceed the largest volume of an assortment if volume is transported from ejector box e to storage box s at all. The next constraints (17) make sure that the capacity of each storage box s is not exceeded. Constraints (18) and (19) define the binary variables.
2.4 Real world decision rules
The aim of this work was to generate a system which offers a solution applicable to industry of the box assignment problem in log yards. This leads to an algorithm based on simple iterative Excel spreadsheet calculation models. A series of inter connected spreadsheets containing transportation time, transportation distance, manual blocking, box width and further exclusion criteria as for instance minimum and maximum values for box width and single usage criterion were generated. As described beforehand, the objective function is to minimize the transportation time (i.e. the total transportation distance). At the same time, a good schedule includes a perfect framework which was analyzed in terms of feeding volume and second by means of the box size adaption.
Heuristics
The heuristics starts with data generation. Transportation times of every possible combination in terms of ejector, storage box and assortment, were combined in a matrix. The restrictions of the volume of assortment a excluded certain combinations from the beginning on. The assortment was ordered by size according to the number of trips given by the volume of an assortment. Starting with the assortment with the most trips the minimum transportation time was chosen from these combinations and ejector, storage box and assortment were blocked for the following selection process.
A0 = A
sort A0 according to Na
while A0 ≠ { } do
for i ∈ A0 do
find minimal transportation time TMs
move(pick s ∈ S) is forbidden
assign corresponding assortment i to box s
remove i from A0
end for
end while
To solve the different steps of the double-stage model the corresponding transportation matrix (TMs and TSes), containing transportation time, distances and transportation counts, has to be considered.
3 Results
3.1 Numerical experiments
For conducting our experiments we reorganize the log yard and change the number of boxes from 42 to 28 (see Fig. 3) and adapt their sizes accordingly.
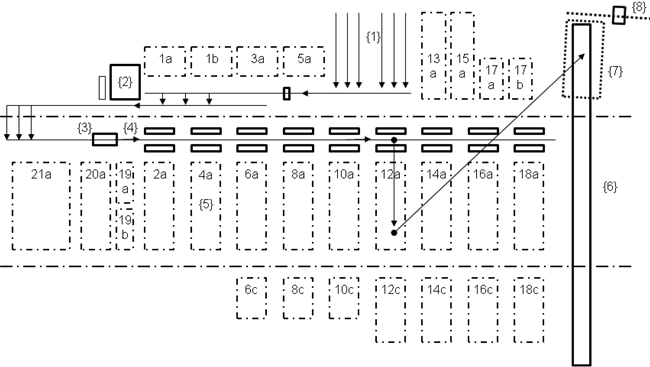
Fig. 3. Rearranged log yard.
The change of the storage area introduces the possibility of working in day shifts excluding the necessity to change the assortment during one day shift.
This reduces downtime significantly as an assortment change yields a time range from 5 to 30 minutes. Usually, changing from one dimension to another leads to a stop in production and additional costs for both machines and personnel. Data used in our experiments are the box size of the storage boxes, the transportation capacity and transportation moves per assortment.
When comparing the values in Table 1 it is easy to see that the assortment with the minimal volume exceeds the capacity of the smallest storage box. Furthermore, also the assortment with the largest volume tops the capacity of the biggest storage box in the case of the original setting. Therefore, the reduction and the amalgamation of the storage boxes were necessary to implement a model without fragmentation of the assortments into several storage boxes. To verify this model the partition model was constructed and it was also used to test the approach of the reduction of storage boxes previously. In addition it should be noted that the numbers of moves per assortment vary from 21 to 68. Hence, shorter transportation times are more important for the assortments with more moves per shift. The real life decision rule was implemented in Excel, while Xpress was used for solving the optimization models.
| Table 1. Minimal and maximal values of volume, number of moves and capacity in the new and original problem with 28 and 42 storage boxes. | ||
| Minimum | Maximum | |
| Va | 5.46 | 12.20 |
| Na | 21 | 68 |
| C28 | 4.1 | 12.3 |
| C42 | 4.0 | 10.6 |
3.2 Comparison of results
To evaluate the quality of both the proposed heuristic and the optimization based approaches, the results are compared with a solution which is obtained by classic manual planning. The original planning model was done by a paper plan where free boxes were used while full boxes were blocked. By comparing the results of the methods presented in this paper with the solution given by the original approach, the value of the proposed method is appraisable.
Table 2 provides the solution obtained by different approaches. The number of trips per assortment is shown in the second column. The notation indicates the solution i.e. the assignment of an assortment to ejector box/storage box. Assortments 1, 2 and 3 have not been assigned to a storage box because they refer to oversize, undersize and metal containing logs. When comparing the transportation time which is the total time needed to perform one production cycle (15 days) it is evident that the method of choice for an optimized log yard is the partition model, even though the computational time has to be considered. Moreover, note that the detour of previously rearranging the log yard leads to an increase of the solution by 1.6 percent which can be seen by comparing the results of the partition model with 28 and 42 storage boxes. This estimate of the improvement, given by the yard redesign, can be explained by the additional storage capacity, which is allocated by box combination and also enlargement of two boxes. All the optimized values show significant better results than the manual planning. In the table the third column presents the manual planning. The next column shows the heuristic approach in Excel. The remaining columns display the solutions gained with Xpress for the double-stage and partition model with 28 and 42 storage boxes. In the columns the ejector box and the storage box are given in dependence of the assortment.
| Table 2. Comparable solutions of the log yard and box assignment problem. | ||||||
| Assortment | Number of trips | Original | Excel double-stage | Xpress double-stage | Xpress partition | Xpress partition |
| 1 | - | 1/- | 1/- | 1/- | 1/- | 1/- |
| 2 | - | 2/- | 2/- | 2/- | 2/- | 2/- |
| 3 | - | 3/- | 3/- | 3/- | 3/- | 3/- |
| 4 | 68 | 12/12 a | 17/16 c | 18/18 a | 18/18 a | 18/18 a, 18c |
| 5 | 54 | 8/8 a | 11/18 c | 14/18 c | 17/17 b, 18 c | 17/17 b, 18d |
| 6 | 44 | 2/2 a | 9/17 b | 17/17 b | 15/17 a | 15/17 a |
| 7 | 56 | 16/16 a | 18/18 a | 16/16 a | 16/16 a | 16/16 a, 18 b |
| 8 | 44 | 10/10 a | 10/14 c | 12/16 c | 11/13 a | 12/14 b, 16 c |
| 9 | 37 | 4/4 a | 8/12 c | 10/14 c | 12/16 c | 13/6 c, 15 a |
| 10 | 46 | 17/17 a, b | 16/16 a | 11/14 a | 14/14 a | 14/14 a, 16 b |
| 11 | 36 | 9/10 c | 7/10 a | 8/12 c | 10/14 c | 9/12 a, 16 d |
| 12 | 30 | 6/6 a | 6/10 c | 6/10 c | 6/10 c | 11/8 c, 13 a |
| 13 | 46 | 13/13 a | 13/15 a | 13/15 a | 13/15 a | 10/12 b, 14 c, d |
| 14 | 36 | 18/18 a | 14/14 a | 9/12 a | 9/12 a | 7/10 a, 10 b |
| 15 | 30 | 11/12 c | 5/8 a | 7/10 a | 8/12 c | 8/12 c, 12 d |
| 16 | 32 | 15/15 a | 15/13 a | 15/13 a | 7/5 a, 10 a | 6/8 b, 10 c |
| 17 | 25 | 14/14 a | 12/12 a | 5/8 a | 5/8 a | 5/5 a, 8 a |
| 18 | 21 | 7/8 c | 4/8 c | 4/8 c | 4/6 a | 4/6 a, 6 b |
| # storage boxes | 42 | 28 | 28 | 28 | 42 | |
| Transportation time (min) | - | 342.8 | 326.3 | 301.5 | 288.1 | 293.6 |
| Computational time | - | - | - | 0.0 sec | 106.3 sec | approx. 6 days |
| Saving | - | - | 4.8 % | 12.1 % | 16.0 % | 14.4 % |
The comparably easy approach of the Excel heuristic already reduces the transportation time by 15 minutes and shows a decent improvement to the existing solution. Even better results are gained by using Xpress for the optimization. The Xpress double-stage model performs with an improved time of 12.1 percent while the best result with a time improvement of 16.0 percent is gained with the Xpress partition model in combination with pooled boxes and additionally the ability of using multiple storage boxes for one assortment. When comparing the heuristic to the models with 28 storage boxes the improvement of 11.2 percent is due to the optimization. Using the old log yard layout with 42 storage boxes and allowing multiple storage boxes for each assortment an improvement of 14.4 percent is possible. This solution is reached when reducing the gap between lower bound and best solution to 0.15 percent that is approximately 30 seconds transportation time. Comparing the two partition models indicates the benefit of previously reducing the number of storage boxes. The last model was just investigated to demonstrate the superiority of previously reducing the number of boxes. On no account should this be taken as an optimization model, however it serves for comparative purposes. Note, that after 20 minutes running time a solution with a gap below one percent to the lower bound is found. Therefore, when taking a practically worthwhile stopping criteria for the optimization the computational time of the presented model can be reduced to approx. 30 minutes and the model can be used in practice. Table 3 shows the improvement of the bound and gap on the solution of the partition model.
| Table 3. Best bound and gap on the best solution of 293.979 minutes, which is found after 20 minutes, of the partition model with 42 storage boxes. | ||
| Best bound | Gap | |
| 30 min | 291.311 | 0.91% |
| 60 min | 291.537 | 0.83% |
| 90 min | 291.658 | 0.79% |
| 120 min | 291.744 | 0.76% |
| 180 min | 291.855 | 0.72% |
| 240 min | 291.932 | 0.70% |
The partition model with 42 storage boxes has 1158 constraints and 12 366 variables. Due to the related transportation distances, the similar volumes of the assortments and the alike capacities of the storage boxes the solution space is rather flat and proofing optimality is hard. Nevertheless, when reducing the gap to 0.5 percent the solution of 293.585 minutes can be found after approximately one day. A gap of 0.5 percent causes 90 seconds difference of the best bound and lowest transportation time. Moreover, the solution is not improved when reducing the gap even further to 0.15 percent. The received saving numbers are due to two factors: First the changed log yard layout and second the optimization approach. The maximum time reduction can be achieved when the log yard is optimized to 28 storing boxes and the calculation is performed with the Xpress partition model. All computations where performed on an Intel Core I7 3930K computer with 64 GB RAM. Nevertheless, the standard settings of Xpress 7.3 have not been changed and no tuning was investigated.
4 Discussion
The box assignment problem on a log yard has been modeled in a new way which guarantees a production optimized and time transparent solution. The model is flexible enough to deal with variations of the production volume and intermittent blocked boxes. The solution methods of the problem are adapted to the variations, corresponding to the changes. From the test results it is evident, that both models, double-stage and partition algorithm, facilitate a solution superior than those achieved by manual planning. Even more the deviation of the partition model with Xpress shows that reducing the number of storage boxes leads to an improved solution.
Future work should be performed on building a model which is flexible in terms of varying demand of the raw material. For a validation of the build model, the gained data has to be compared with real data as in practical application it is possible to confirm the exact generation of the optimization models. In this paper the model is based on feeding data and log storage yard spacing regulations meeting direct production data in contrast to theoretical approaches, which do not take advantage of structures in the problem data. Nevertheless, the model presented in this paper shows a valuable way of solving logistic problems in wood products industry.
References
Adams E. (1984). DESIM: a system for designing and simulating hardwood sawmill systems. US Department of Agriculture, Forest Service, Northeastern Forest Experiment Station.
Baesler F.F., Moraga M., Ramis F.J. (2002). Productivity improvement in the wood industry using simulation and artificial intelligence. In: Proceedings of the 34th conference on Winter simulation: exploring new frontiers. p. 1095–1098.
Baesler F.F., Araya E., Ramis F.J., Sepúlveda J.A. (2004). The use of simulation and design of experiments for productivity improvement in the sawmill industry. In: Proceedings of the 36th conference on Winter simulation. p. 1218–1221.
Dogan C.A., McClain T.F., Wicklund S.A. (1997). Simulation modeling and analysis of a hardwood sawmill. Simulation Practice and Theory 5(5): 387–403. http://dx.doi.org/10.1016/S0928-4869(96)00021-3.
Dohn A., Clausen J. (2010). Optimizing the slab yard planning and crane scheduling problem using a two-stage heuristic. International Journal of Production Research 48(15): 4585–4608. http://dx.doi.org/10.1080/00207540902998331.
Fronius K. (1989). Arbeiten und Anlagen im Sägewerk – Band 2 Spaner, Kreissägen und Bandsägen. DRW-Verlag, Leinfelden-Echterdingen.
Fronius K. (1991). Arbeiten und Anlagen im Sägewerk – Band 3 Gatter, Nebenmaschinen, Schnitt- und Restholzbehandlung. DRW - Verlag, Leinfelden- Echterdingen.
Greigeritsch T. (2009). Neue Methoden zur Planung und Optimierung der Schnittholzproduktion von Nadelholzsägewerken. Gabler Research, Wiesbaden. http://dx.doi.org/10.1007/978-3-8349-8409-8.
Greigeritsch T., Gronalt M., Teischinger A. (2007). Short and medium term production planning and material flow simulation in sawmilling industry. In: Modelling the wood chain: foresty – wood industry – wood product markets, 17.–19. September 2007, Helsinki.
Gronalt M., Greigeritsch T. (2008). Stoffstrombasiertes Produktionsmanagement für Sägebetriebe. Fabrik der Zukunft.
Hirsch P., Palfi A., Gronalt M. (2012). Solving a time constrained two-crane routing problem for material handling with an ant colony optimization approach: an application in the roof-tile industry. International Journal of Production Research 50(20): 6005–6021. http://dx.doi.org/10.1080/00207543.2011.640957.
Kyle R.G., Ludka C.R. (2000). Simulating the furniture industry. In: Proceedings of the 2000 Winter Simulation Conference. p. 1347–1350. http://dx.doi.org/10.1109/WSC.2000.899107.
Mendoza G.A., Meimban R.J., Araman P.A., Luppold W.G. (1991). Combined log inventory and process simulation models for the planning and control of sawmill operations. In: Proceedings of the 23rd CIRP International Seminar on Manufacturing Systems.
Ramis F., Jarpa R., Palma J., Sánchez J., Baesler F., Sepúlveda J. (2004). Bottleneck analysis using simulation. American institute of industrial engineering. Proceedings of Simulation Solutions 2004.
Randhawa S.U., Brunner C.C., Funck J.W., Zhang G. (1994). A discrete event object-oriented modeling environment for sawmill simulation. Simulation 62(2): 119–130. http://dx.doi.org/10.1177/003754979406200206.
Todoroki C., Rönnqvist M. (2002). Dynamic control of timber production at a sawmill with log sawing optimization. Scandinavian Journal of Forest Research 17: 79–89. http://dx.doi.org/10.1080/028275802317221118.
Wagenführ A., Scholz F. (2008). Taschenbuch der Holztechnik. Carl Hanser Verlag, München.
Yanasse H.H., Limeira M.S. (2006). A hybrid heuristic to reduce the number of different patterns in cutting stock problems. Computers & Operations Research 33: 2744–2756. http://dx.doi.org/10.1016/j.cor.2005.02.026.
Total of 18 references

