Geographic variations of wood properties of Larix sibirica naturally grown in Mongolia
Tumenjargal B., Ishiguri F., Aiso-Sanada H., Takahashi Y., Baasan B., Chultem G., Ohshima J., Yokota S. (2018). Geographic variations of wood properties of Larix sibirica naturally grown in Mongolia. Silva Fennica vol. 52 no. 4 article id 10002. https://doi.org/10.14214/sf.10002
Highlights
- Significant differences (p < 0.01) among five stands were found in tree height, stress-wave velocity of stems, dynamic Young’s modulus of stems and logs, annual ring width, and latewood percentage, suggesting that there was geographic variation of mechanical properties of wood in Larix sibirica (Münchh.) Ledeb. grown in Mongolia
- Dynamic Young’s modulus of logs in L. sibirica trees can be predicted by stress-wave velocity of stems
- Stem diameter of L. sibirica naturally grown in Mongolia is closely related to radial growth at initial stage of growth, especially within the first twenty years.
Abstract
Geographic variations in growth, stress-wave velocity of stem, dynamic Young’s modulus of stems and logs, annual ring width, latewood percentage and basic density were investigated for Larix sibirica (Münchh.) Ledeb. naturally grown in Mongolia. A total of 250 trees with 20 to 30 cm in stem diameter at a height of 1.3 m above ground level were selected from each natural stand in five different provenances in Mongolia. In addition, five trees in each stand were cut for measuring dynamic Young’s modulus of stems and logs, annual ring width, latewood percentage and basic density. Mean values of stress-wave velocity of stems in each stand ranged from 2.92 to 3.41 km s–1, and the mean value of five stands was 3.23 km s–1. Mean values of dynamic Young’s modulus of logs in each stand ranged from 5.17 to 9.72 GPa. A significant correlation (r = 0.798, p < 0.01) was found between stress-wave velocity of stems and dynamic Young’s modulus of logs. Among the five stands, the highest and the lowest values of average annual ring number were 193 and 44, respectively. Mean values of basic density in five trees within each stand were examined and ranged from 0.52 to 0.56 g cm–3. Significant differences among five stands were found in tree height, stress-wave velocity of stem, dynamic Young’s modulus of stems and logs, annual ring width and latewood percentage, suggesting that L. sibirica trees naturally grown in Mongolia have geographic variations in mechanical properties of wood.
Keywords
natural forests;
basic density;
dynamic Young’s modulus;
nondestructive testing;
stress-wave velocity
- Tumenjargal, Faculty of Agriculture, Utsunomiya University, Utsunomiya, Tochigi 321-8505, Japan; United Graduate School of Agricultural Science, Tokyo University of Agriculture and Technology, Fuchu, Tokyo 183-8509, Japan; Research and Training Institute of Forestry and Wood Industry, Mongolian University Science and Technology, Ulaanbaatar 14191, Mongolia E-mail t_bayasaa88@yahoo.com
-
Ishiguri,
Faculty of Agriculture, Utsunomiya University, Utsunomiya, Tochigi 321-8505, Japan
E-mail
ishiguri@cc.utsunomiya-u.ac.jp

- Aiso-Sanada, Forestry and Forest Products Research Institute, Tsukuba, Ibaraki 305-8687, Japan E-mail haiso@ffpri.affrc.go.jp
- Takahashi, Faculty of Agriculture, Utsunomiya University, Utsunomiya, Tochigi 321-8505, Japan E-mail zo.r.by0814@gmail.com
- Baasan, Research and Training Institute of Forestry and Wood Industry, Mongolian University Science and Technology, Ulaanbaatar 14191, Mongolia E-mail bayartsetseg@must.edu.mn
- Chultem, Research and Training Institute of Forestry and Wood Industry, Mongolian University Science and Technology, Ulaanbaatar 14191, Mongolia E-mail ganbaatar_ch@must.edu.mn
- Ohshima, Faculty of Agriculture, Utsunomiya University, Utsunomiya, Tochigi 321-8505, Japan E-mail joshima@cc.utsunomiya-u.ac.jp
- Yokota, Faculty of Agriculture, Utsunomiya University, Utsunomiya, Tochigi 321-8505, Japan E-mail yokotas@cc.utsunomiya-u.ac.jp
Received 16 May 2018 Accepted 8 November 2018 Published 12 November 2018
Views 79707
Available at https://doi.org/10.14214/sf.10002 | Download PDF

1 Introduction
The genus Larix consists of about ten species and these species are distributed throughout the northern hemisphere (Cáceres et al. 2018). Wood resources of these species obtained from both natural stands and plantations have good physical and mechanical properties as well as high decay resistance (Koizumi et al. 1990, 2003, 2005; Takada et al. 1992; Zhu et al. 2000; Gierlinger et al. 2004; Venäläinen et al. 2006; Ishiguri et al. 2008; Luostarinen 2011; Fukatsu et al. 2015; Neverov et al. 2017; Cáceres et al. 2018). In Mongolia, Larix sibirica (Münchh.) Ledeb. forests cover more than 7.2 million hectares, accounting for over 60% of the forested area and about 80% of the wood stock in the country (Forest Study and Development Center, Ministry of Green Development and Tourism, Mongolia 2016). Therefore, L. sibirica is considered to be the most important forestry species in Mongolia as well as European countries.
The geographical variations of Larix species have been investigated for growth characteristics and wood properties (Toda and Mikami 1976; Park and Fowler 1983; Takada et al. 1992; Abaimov et al. 2002; Koizumi et al. 2003, 2005; Kuz’mina 2004; Lukkarinen et al. 2009; Batkhuu et al. 2010; Dulamsuren et al. 2011; Nagamitsu et al. 2014; Fedorkov 2014; Neverov et al. 2017; Cáceres et al. 2018). In wood properties, Cáceres et al. (2018) investigated the variation in selected mechanical properties in 12-year-old trees from 20 different provenances of L. kaempferi (Lamb.) Carrière planted in Quebec, Canada. They reported that the mechanical properties of wood from all provenances showed significant differences. Koizumi et al. (2003) also reported that wood density of L. sibirica significantly differed among five natural stands in South-Central Siberia, Russia.
Several researchers have reported on the nondestructive testing methods for evaluating Young’s modulus of wood (Sobue 1986; Arima et al. 1993; Takata and Hirakawa 2000; Tsehaye et al. 2000; Nagao et al. 2003; Carter et al. 2005; Grabianowski et al. 2006; Wang et al. 2007; Wessels et al. 2011). For example, stress-wave velocity of stems in standing trees is known as one of the major measurement methods for evaluating mechanical properties of logs or lumber (Ishiguri et al. 2008). Dynamic Young’s modulus of logs measured by tapping method is also used for evaluating mechanical properties of lumber (Sobue 1986; Arima et al. 1993; Takata and Hirakawa 2000; Nagao et al. 2003; Ishiguri et al. 2008).
This study aimed to determine geographic variations of growth characteristics (stem diameter and tree height), stress-wave velocity of stem, dynamic Young’s modulus of stems and logs, annual ring width, latewood percentage and basic density of L. sibirica naturally grown in Mongolia.
2 Materials and methods
2.1 Sampling stands
Five natural forests of L. sibirica were selected from five different provenances in Mongolia: Khentii, Arkhangai, Zavkhan, Khuvsgul, and Selenge. Table 1 shows geographic and climatic information for the five sampling stands. These five stands are located in the natural distribution area of L. sibirica. All stands, except for stand Selenge, were pure stands of L. sibirica, while stand in Selenge was a mixed stand consisting of L. sibirica and Betula platyphylla Sukaczev. A total of 250 standing trees (50 trees in each stand) with stem diameters ranging from 20 to 30 cm at a height of 1.3 m above ground level were selected from the five stands for measuring growth characteristics and stress-wave velocity of stem. In addition, five trees with good stem shape without any severe damages were selected in each stand for measuring dynamic Young’s modulus of logs, annual ring width, latewood percentage and basic density.
| Table 1. Geographic and climatic information on the sampling stands in the present study. | |||||||||
| Provenance | Town | Latitude, Longitude | Above sea level (m) | Annual temperature (°C) | Annual precipitation (mm year–1) | ||||
| Mean | Min. (Jan.) | Max. (Jul.) | Mean integrated value | Min. | Max. | ||||
| Khentii | Batshireet | 48°51´N, 110°05´E | 1214 | –1.6 | –27.2 | 19.2 | 368 | 0 (Jan.) | 160 (Jul.) |
| Arkhangai | Tsenker | 47°22´N, 101°43´E | 1707 | 0.5 | –19.9 | 17.4 | 377 | 0 (Jan.) | 150 (Aug.) |
| Zavkhan | Tosontsengel | 48°41´N, 98°17´E | 1878 | –5.0 | –36.1 | 17.7 | 242 | 1 (Feb.) | 92 (Aug.) |
| Khuvsgul | Jargalant | 48°31´N, 99°15´E | 1827 | –1.8 | –29.1 | 18.3 | 226 | 0 (Feb.) | 141 (Aug.) |
| Selenge | Mandal | 48°41´N, 106°52´E | 1120 | 0.2 | –27.2 | 22.4 | 271 | 0 (Mar.) | 157 (Aug.) |
| Min., minimum; Max., maximum. Data on annual temperature and precipitation were provided from Information and Research Institute of Meteorology, Hydrology and Environment, Mongolia. Mean annual temperature was calculated by averaging monthly temperature obtained from 2012 to 2016. Mean integrated values of precipitation were calculated by integrating monthly precipitation values of one year (2012 to 2016), and then averaged integrated values of five years. | |||||||||
2.2 Growth characteristics and stress-wave velocity of stem
Stem diameter, tree height, and stress-wave velocity of stem were measured for all the selected 250 trees. Trees with abnormal values of stress-wave velocity in radial direction were omitted to avoid using trees with decayed stems as samples. Stress-wave propagation time was determined by using a commercial handheld stress-wave timer (Fakopp Microsecond Timer, Fakopp Enterprise) according to the method described by Ishiguri et al. (2008). To measure stress-wave velocity for longitudinal direction, the start and stop sensors were set at 1.5 and 0.5 m above ground respectively. A small hammer was used to hit the start sensor, creating a stress wave. The stress-wave propagation time was recorded between the start and stop sensors. Six measurements for stress-wave propagation time were made at same position from each standing tree. The stress-wave velocity was calculated by dividing the distance between two sensors by the average value of stress-wave propagation time.
2.3 Dynamic Young’s modulus of stems and logs
Total 25 trees (five trees in each stand) were selected to cut. Before cutting trees, stress-wave velocity of stems was measured for these 25 selected trees. Dynamic Young’s modulus of stems (DMOES) was calculated by the following formula:
![]()
where ρ is mean values of green density of logs collected from a tree (kg m–3), V is stress-wave velocity of stem (km s–1).
After cutting trees, logs with 2 m length were obtained from 1.3 m above the ground until the top diameter of each log was less than 14 cm. A total of 111 logs were collected from 25 trees (five trees in each stand, 3 to 6 logs from a tree). Green weight and dimensions of logs included bark were measured by portable electric balance and, diameter tape and tape measure, respectively. Then, green density of logs was calculated by dividing green weight by green volume calculated from measured dimensions. Dynamic Young’s modulus of logs was determined by tapping method (Sobue 1986). The cross end of each log was tapped by a small hammer, and then first resonance frequency was determined by a handheld fast Fourier transform (FFT) analyzer (AD-3527, A&D) with an accelerometer (PV-85, Rion) set on the other end of each log. The dynamic Young’s modulus of the log (DMOEL) was calculated by the following formula:
![]()
where l is the length of the log (m), f is the first resonance frequency (Hz), and ρ is the green density of the log (kg m–3).
2.4 Annual ring width and latewood percentage
In order to measure the annual ring and latewood width, logs of 0.5 m in length were obtained from 0.8 to 1.3 m above ground level of 25 harvested trees. Radial boards with 30 mm in thickness (including bark to bark) were obtained from the logs. Then, bark to bark strips 20 mm in thickness were prepared. The image data (1200 dpi) of the transverse sections of the strips from pith to bark in one direction were captured by a personal computer with a scanner (GT-9300UF, EPSON). Both annual ring and latewood width were measured using the software ImageJ (National Institute of Health, USA).
2.5 Basic density
Disks with 1 cm thickness were obtained at 1.3 m above ground level of 25 harvested trees. Wedge-shape specimens with 30° center angel were collected from the disk. The wedge-shape specimens were cut again at 1 cm intervals from pith to bark. Green weight was measured by electronic balance and green volume was determined by water displacement. Then the cut blocks from the wedge-shape specimens were oven-dried at 105 °C. Basic density was calculated by dividing oven-dry weight by green volume. Mean values from pith to bark in a wedge-shape specimen were calculated as mean values of basic density of a tree.
2.6 Data analysis
All data analysis was conducted by using software (Excel 2016, Microsoft). An analysis of variance (ANOVA) test was applied to evaluate the differences in measured characteristics within-stands. To detect among-stand differences in dynamic Young’s modulus of logs, data obtained from 1.3 to 7.3 m above ground level were used, because logs were obtained from these height positions in all 25 harvested trees. To evaluate radial growth, the relationships were determined between stem diameter and mean annual ring width of certain positions (mean values of annual ring width calculated from ‘1st to 10th’, ‘1st to 20th’, ‘1st to 30th’, ‘1st to 40th’, ‘11st to 20th’, ‘21st to 30th’, and ‘31st to 40th’ annual ring from pith, respectively).
3 Results
Table 2 shows the mean values of growth characteristics and stress-wave velocity of stems of standing trees. The mean values of stem diameter, tree height and stress-wave velocity in a total of 250 standing trees were 24.0 cm, 15.8 m, and 3.23 km s–1, respectively. Although the stem diameter was almost the same in all stands, the mean values of tree height and stress-wave velocity of stems were significantly different among the five stands. Mean tree height ranged from 12.2 to 19.7 m. The mean stress-wave velocity of stem in five stands was 3.23 km s–1 ranging from 2.92 (Arkhangai) to 3.41 km s–1 (Selenge). A weak significant correlation was found between stem diameter and stress-wave velocity of stems (r = –0.402, p < 0.01) for 250 standing trees (Fig. 1).
| Table 2. Growth characteristics and stress-wave velocity of stems in Larix sibirica trees. | |||||||
| Provenance | n | D (cm) | TH (m) | SWV (km s–1) | |||
| Mean | SD | Mean | SD | Mean | SD | ||
| Khentii | 50 | 24.8 | 2.2 | 19.7 | 1.1 | 3.20 | 0.31 |
| Arkhangai | 50 | 26.5 | 2.5 | 12.2 | 1.5 | 2.92 | 0.19 |
| Zavkhan | 50 | 23.3 | 2.2 | 15.9 | 1.9 | 3.27 | 0.33 |
| Khuvsgul | 50 | 22.7 | 1.9 | 15.1 | 1.7 | 3.34 | 0.32 |
| Selenge | 50 | 22.6 | 2.0 | 16.2 | 1.8 | 3.41 | 0.40 |
| Mean/total | 250 | 24.0 | 1.7 | 15.8 | 2.7 | 3.23 | 0.19 |
| F-value | - | 136.307 | 18.210 | ||||
| p-value | <0.01 | <0.01 | |||||
| n, number of standing trees; D, stem diameter at 1.3 m above ground level; TH, tree height; SWV, stress-wave velocity of stems; SD, standard deviation. F and p-values were obtained by analysis of variance (ANOVA) test. | |||||||

Fig. 1. Relationship between stem diameter at 1.3 m above ground level and stress-wave velocity (SWV) of stems in all standing trees. n, number of trees; r, correlation coefficient; **, p < 0.01.
Mean values of dynamic Young’s modulus of logs harvested at three height positions were 7.79, 7.72 and 7.34 GPa for 1.3–3.3 m, 3.3–5.3 m, and 5.3–7.3 m of the height positions, respectively (Table 3). In each stand, the mean values of logs harvested at three height positions ranged from 5.17 to 9.97 GPa. Except for logs from Khuvsgul, dynamic Young’s modulus slightly decreased from the bottom to the top of the logs, whereas longitudinal variation of dynamic Young’s modulus of logs from Khuvsgul showed almost constant values toward the top (Fig. 2). The mean values of all logs in each stand varied from 5.17 (Arkhangai) to 9.72 (Selenge) GPa (Fig. 2). The mean value and standard deviation of 111 logs (from 25 trees 3 to 6 logs in each tree) were 7.44 and 1.64 GPa, respectively.
| Table 3. Dynamic Young’s modulus (GPa) of logs in three height positions of Larix sibirica trees. | ||||||||
| Provenance | Height position (m) | Total | ||||||
| 1.3–3.3 | 3.3–5.3 | 5.3–7.3 | ||||||
| Mean | SD | Mean | SD | Mean | SD | Mean | SD | |
| Khentii | 8.39 | 1.50 | 8.48 | 0.93 | 8.11 | 0.83 | 8.32 | 0.19 |
| Arkhangai | 5.75 | 0.75 | 5.32 | 0.92 | 4.43 | 0.41 | 5.17 | 0.67 |
| Zavkhan | 7.54 | 1.74 | 7.52 | 1.94 | 6.99 | 2.14 | 7.35 | 0.31 |
| Khuvsgul | 7.54 | 0.49 | 7.11 | 0.65 | 7.18 | 0.17 | 7.28 | 0.23 |
| Selenge | 9.75 | 0.52 | 10.16 | 0.88 | 10.00 | 1.40 | 9.97 | 0.20 |
| Mean/total | 7.79 | 1.46 | 7.72 | 1.78 | 7.34 | 2.02 | 7.62 | 1.75 |
| F-value | 8.359 | 11.851 | 13.606 | 36.118 | ||||
| p-value | <0.01 | <0.01 | <0.01 | <0.01 | ||||
| SD, standard deviation. F and p-values were obtained by analysis of variance (ANOVA) test. Number of logs at each height position of a stand was 5. Mean value of total in each stand was calculated by averaging the values of 15 trees harvested from a stand. | ||||||||

Fig. 2. Longitudinal variations of dynamic Young’s modulus of logs in Larix sibirica in each stand. SD, standard deviation; n, number of logs. Open circles indicate the data on the individual logs collected at different height positions of stem from five harvested trees in each stand. Mean value and standard deviation of all logs (n = 111) were 7.44 and 1.64 GPa, respectively.
The growth characteristic, stress-wave velocity, dynamic Young’s modulus of stems, number of annual ring, annual ring width, latewood percentage and basic density of the harvested trees are presented in Table 4. The mean values of stem diameter, thee height and stress-wave velocity of sample trees were almost the same as those in 250 trees (Table 2). The mean values of dynamic Young’s modulus of stems were vary among stands. The highest and lowest values were found in Selenge (10.14 GPa) and in Arkhangai (6.72 GPa), respectively. Mean values of dynamic Young’s modulus of stems were higher than mean values of dynamic Young’s modulus of logs (Fig. 2). Annual ring numbers of the harvested trees ranged from 44 to 193 (Table 4). The mean values of annual ring width were 1.55, 2.47, 0.49, 1.86 and 1.74 mm for Khenii, Arkhangai, Zavkhan, Khuvsgul and Selenge, respectively. Among the five stands, the highest and the lowest values of average annual ring number and latewood percentage were found in Zavkhan (193 annual ring number and 33.2%) and Arkhangai (44 annual ring number and 22.2%), respectively. Mean annual ring width ranged from 0.49 to 2.47 mm. As shown in Fig. 3, annual ring width increased until around 15th to 20th from pith, and then decreased toward the bark side except for stands in Zavkhan and Selenge. For stand in Zavkhan, annual ring width showed almost constant values from pith to bark and for stand in Selenge, annual ring width from pith decreased from the 15th to the 35th annual ring, and then increased again towards the bark side, respectively.
| Table 4. Growth characteristics, stress-wave velocity of stems, and wood properties in harvested Larix sibirica trees. | |||||||||||||||||
| Provenance | n | D (cm) | TH (m) | SWV (km s–1) | DMOES (GPa) | NAR | ARW (mm) | LWP (%) | BD (g cm–3) | ||||||||
| Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | ||
| Khentii | 5 | 25.2 | 0.3 | 19.5 | 1.4 | 3.05 | 0.12 | 6.80 | 0.82 | 72 | 5 | 1.55 | 0.08 | 32.2 | 3.3 | 0.56 | 0.05 |
| Arkhangai | 5 | 26.6 | 0.2 | 11.6 | 1.2 | 2.87 | 0.12 | 6.72 | 0.62 | 44 | 4 | 2.47 | 0.56 | 22.2 | 3.1 | 0.53 | 0.01 |
| Zavkhan | 5 | 23.6 | 0.2 | 15.9 | 1.0 | 3.27 | 0.29 | 7.84 | 1.78 | 193 | 6 | 0.49 | 0.05 | 33.2 | 3.5 | 0.55 | 0.03 |
| Khuvsgul | 5 | 22.5 | 0.3 | 15.1 | 0.7 | 3.24 | 0.14 | 8.41 | 0.67 | 49 | 5 | 1.86 | 0.20 | 26.4 | 2.7 | 0.52 | 0.02 |
| Selenge | 5 | 22.5 | 0.2 | 17.3 | 2.7 | 3.55 | 0.26 | 10.14 | 1.85 | 52 | 8 | 1.74 | 0.23 | 31.0 | 3.6 | 0.54 | 0.02 |
| Mean/Total | 25 | 24.1 | 1.8 | 15.9 | 2.9 | 3.20 | 0.26 | 7.98 | 1.40 | 1.62 | 0.72 | 29.0 | 4.6 | 0.53 | 0.02 | ||
| F-value | - | 16.978 | 7.958 | 6.065 | - | 31.579 | 9.737 | 1.360 | |||||||||
| p-value | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | 0.282 | |||||||||||
| n, number of harvested trees; D, stem diameter at 1.3 m above ground; TH, tree height; SWV, stress-wave velocity of stem; DMOES, dynamic Youngs modulus of stem; NAR, number of annual ring; ARW, annual ring width; LWP, latewood percentage; BD, basic density; SD, standard deviation. F and p-values were obtained by analysis of variance (ANOVA) test. | |||||||||||||||||
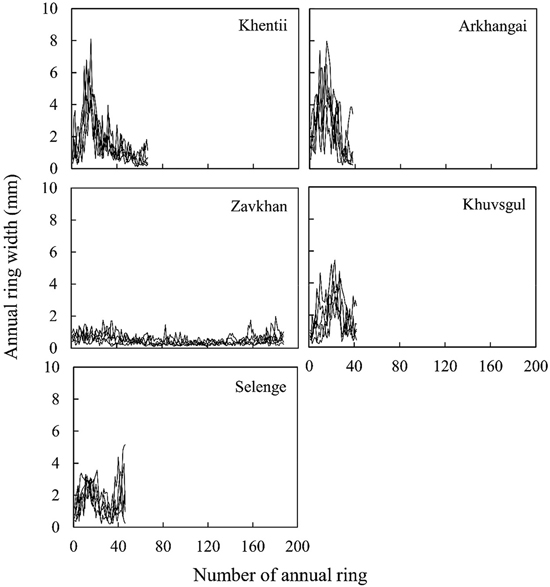
Fig. 3. Radial variations of annual ring width for five sample trees in each stand.
Mean values of basic density in each stand ranged from 0.52 to 0.56 g cm–3, and the mean values of five stands was 0.53 g cm–3 (Table 4). As shown in Fig. 4, mean values of basic density were gradually increased from pith to bark side, and then it showed peak values. After that, it slightly decreased in all stands except for Khuvsgul. For Khuvsgul, basic density showed almost constant values from pith to bark.
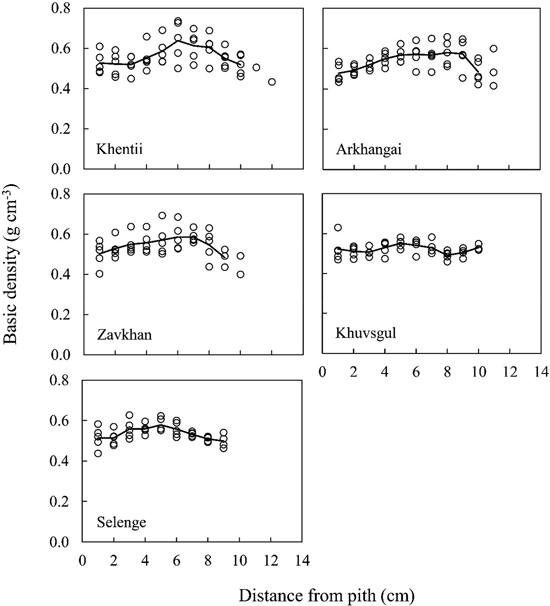
Fig. 4. Radial variations of basic density for five sample trees in each stand. Open circles indicate the data on the individual trees at 1.3 m above ground level. Solid lines indicate mean values of five trees.
Correlation coefficients between stem diameter and mean annual ring width between certain radial positions are shown in the Table 5. Significant correlation coefficients (p < 0.01) were found between stem diameter and mean annual ring width were calculated between mean values of ‘1 to 10’, ‘1 to 20’, ‘1 to 30’, and ‘1 to 40’ annual ring from pith, respectively. Especially within the twenty years was highly related (r = 0.692, p < 0.01) with stem diameter. On the other hand, mean values of ‘1 to 10’ annual ring from pith was significantly correlated with that of ‘11 to 20’ (r = 0.629, p < 0.01), but not with that from ‘21 to 30’ (r = 0.137, p > 0.05) or from ‘31 to 40’ (r = 0.018, p > 0.05), respectively.
| Table 5. Relationships between stem diameter and mean annual ring width between certain radial positions. | ||
| Factor 1 | Factor 2 | r (n = 25) |
| D | Mean ARW from 1 to 10 | 0.602** |
| Mean ARW from 1 to 20 | 0.692** | |
| Mean ARW from 1 to 30 | 0.613** | |
| Mean ARW from 1 to 40 | 0.557** | |
| Mean ARW 1–10 | Mean ARW from 11 to 20 | 0.629** |
| Mean ARW from 21 to 30 | 0.137ns | |
| Mean ARW from 31 to 40 | 0.018ns | |
| r, correlation coefficient; n, number of samples; D, stem diameter; ARW, annual ring width; **, p < 0.01; ns, p > 0.05. | ||
Table 6 shows correlation coefficients among wood properties. Latewood percentage was significantly related to basic density (r = 0.447, p < 0.05), dynamic Young’s modulus (r = 0.493, p < 0.05), and annual ring width (r = –0.681, p < 0.01). In addition, significant positive correlations (r = 0.953, p < 0.01) and (r = 0.798, p < 0.01) was also found between stress-wave velocity of stem and dynamic Young’s modulus of stems, and logs, respectively. On the other hand, dynamic Youngs modulus of stems was closely related (r = 0.729, p < 0.01) to dynamic Young’s modulus of logs.
| Table 6. Correlation coefficients between wood properties. | ||
| Factor 1 | Factor 2 | r (n = 25) |
| BD | SWV | –0.140ns |
| DMOES | –0.202ns | |
| DMOEL | 0.087ns | |
| ARW | –0.132ns | |
| LWP | 0.447* | |
| SWV | DMOES | 0.953** |
| DMOEL | 0.798** | |
| ARW | –0.223ns | |
| LWP | 0.323ns | |
| DMOES | DMOEL | 0.729** |
| ARW | –0.002ns | |
| LWP | 0.106ns | |
| DMOEL | ARW | –0.148ns |
| LWP | 0.493* | |
| ARW | LWP | –0.681** |
| r, correlation coefficient; n, number of samples; BD, basic density; SWV, stress-wave velocity of stem, DMOES, dynamic Young’s modulus of stem; DMOEL, dynamic Young’s modulus of log; ARW, annual ring width; LWP, latewood percentage; **, p < 0.01; *, p < 0.05; ns, p > 0.05 | ||
In the present study, mean values of tree height, stress-wave velocity of stem, dynamic Young’s modulus of stems and logs, annual ring width and latewood percentages differed significantly between the five stands, whereas no significant difference among five stands was found in basic density (Tables 2, 3, and 4).
4 Discussion
4.1 Comparison of measured characteristics with other Larix species
Basic wood properties of Larix species have been reported by many researchers (Koizumi et al. 1990, 2003, 2005; Takada et al. 1992; Takata and Hirakawa 2000; Zhu et al. 2000; Nagao et al. 2003; Karlman et al. 2005; Ishiguri et al. 2008; Luostarinen 2011; Fukatsu et al. 2015; Neverov et al. 2017; Cáceres et al. 2018). Although tree age was different, stress-wave velocity values in L. sibirica (Table 2) were similar or lower to those in L. kaempferi (Ishiguri et al. 2008; Fukatsu et al. 2015). In L. kaempferi, Nagao et al. (2003) reported that dynamic Young’s modulus ranged from 7.15 to 12.93 GPa for 18 logs from four 63-year-old trees. Koizumi et al. (2003) determined dynamic Young’s modulus of 50 logs with 2 m length from 40 to 80-year-old L. sibirica trees, ranging from 7.6 to 10.3 GPa. Mean values of dynamic Young’s modulus of logs obtained in this study (Table 3) similar to those L. sibirica naturally grown in Russia (Koizumi et al. 2003), but relatively lower than those in L. kaempferi (Nagao et al. 2003; Ishiguri et al. 2008).
Karlman et al. (2005) were investigated annual ring width and latewood percentage in five different Larix species. They reported that mean values of annual ring width and latewood percentage were 1.08 mm and 39% for 150-year-old L. sibirica and 1.00 mm and 39% for 120-year-old L. sukaczewii Dylis naturally grown in Russia, 1.92 and 42% for 106-year-old L. decidua Mill. and 3.29 mm and 34% for 35-year-old L. decidua, 3.94 mm and 29% for 35-year-old L. kaempferi planted grown in Sweden, respectively. The results of annual ring width in the present study (Table 4) were similar to those of L. sibirica naturally grown in Russia (Koizumi et al. 2003; Karlman et al. 2005) and were much lower than that for L. decidua and L. kaempferi planted in Sweden, respectively. The mean value of latewood percentage of L. sibirica in the present study (Table 4) was also lower than the results from other researchers (Karlman et al. 2005; Luostarinen 2011).
Mean wood density determined by X-ray densitometry in the young trees was 0.54 g cm–3 for L. decidua and, 0.45 g cm–3 for L. kaempferi, respectively (Karlman et al. 2005). In L. sibirica planted in Finland, mean wood density within a ring in mature heartwood (12% moisture content) determined by X-ray microdensitometry ranged from 0.45 to 0.46 g cm–3 at three different heights (Luostarinen 2011). Although measurement method is different, the results obtained in the present study (Table 4) were lower than those of L. sibirica studied by Koizumi et al. (2003) and Karlman et al. (2005), and higher than L. sibirica planted in Finland (Luostarinen 2011). However, mean basic density values obtained in this study (Table 4) were similar to L. kaempferi trees from 23 provenances in Japan (Koizumi et al. 2005).
4.2 Relationships among measured characteristics
It has been reported that no or weak significant correlations were found between stem diameter and stress-wave velocity or Young’s modulus of stems in softwoods, including Larix species. (Koizumi et al. 1990; Carter et al. 2005; Ishiguri et al. 2008). The correlation observed in L. sibirica trees in the present study (Fig. 1) was the same as that found in previous studies of L. kaempferi.
Significant correlations were found between dynamic Young’s modulus of stems and logs, and stress-wave velocity of stems (Table 6). It has been reported that a significant positive correlation was found between stress-wave velocity of stems and dynamic Young’s modulus of logs in many softwood species, including Larix species (Tsehaye et al. 2000; Nagao et al. 2003; Carter et al. 2005; Wang et al. 2007). Based on the results, it is suggested that dynamic Young’s modulus of logs in L. sibirica can be predicted by stress-wave velocity of stems. Loustarinen (2011) reported that a negative, strong correlations found between the annual ring width and wood density, while no significant correlation observed between annual ring width and latewood percentage at the butt of L. sibirica trees planted in Finland. In the present study, a negative correlation was found between annual ring width and latewood percentage, whereas no correlation was found between annual ring width and basic density (Table 6).
As shown in Table 5, the values of annual ring width in early stage of tree growth closely relates to stem diameter of L. sibirica, suggesting that radial growth in L. sibirica at the initial stage of growth, especially within the first twenty years, is closely related to stem diameter. It is also possible that trees with faster radial growth rates at the initial stage of growth do not always show faster radial growth rates at the later stage of growth.
4.3 Geographic variation of wood properties
It is known that geographical variations are found in growth characteristics and wood properties in Larix species (Toda and Mikami 1976; Park and Fowler 1983; Takada et al. 1992; Koizumi et al. 2003, 2005; Lukkarinen et al. 2009; Batkhuu et al. 2010; Nagamitsu et al. 2014; Fedorkov 2014; Neverov et al. 2017; Cáceres et al. 2018). Takada et al. (1992) reported that among-geographic variations in modulus of elasticity of stems were recognized in L. kaempferi trees planted in provenance-trial stand in Japan. Similar among-geographic variations in L. kaempferi were also found in the mechanical properties of wood (Koizumi et al. 2005; Cáceres et al. 2018). In the present study, as shown in Tables 2, 3 and 4, significant differences in tree height, stress-wave velocity of stem, dynamic Young’s modulus of stems and logs, annual ring width and latewood percentage were found among stands, suggesting that L. sibirica trees naturally grown in Mongolia have geographic variations in the mechanical properties of their wood. On the other hand, no significant difference was found in basic density among five stands, because the relatively larger standard deviation value was found in Khentii (Table 4). Therefore, further research is needed for clarifying the large deviation of basic density values in Khentii.
5 Conclusions
Geographical variations of growth characteristics, stress-wave velocity of stem, dynamic Young’s modulus, annual ring width, latewood percentage, and basic density were investigated for L. sibirica naturally grown at five different stands in Mongolia. Significant differences among five stands were found in all measured characteristics, except for basic density. Stress-wave velocity of stem was significantly correlated with dynamic Young’s modulus of logs in L. sibirica, suggesting that nondestructive stress-wave techniques are considered as useful methods in future wood utilization and tree breeding programs for this species. Based on the results, it is considered that L. sibirica trees naturally grown in Mongolia have geographic variations in the mechanical properties of their wood, suggesting that selection of trees with superior wood property could offer the potential for establishing plantation in Mongolia by conducting suitable tree breeding programs.
Acknowledgements
A part of this research was financially supported by the M-JEED program of the Ministry of Education, Culture and Science, Mongolia. The authors express their appreciation to Mr. Sarkhad Murzabek, Mongolian University of Science for his assistance in the field experiments.
References
Abaimov A.P., Barzut V.M., Berkutenko A.N., Buitink J., Martinsson O., Milyutin L.I., I, Polezhaev A., Putenikhin V.P., Takata K. (2002). Seed collection and seed quality of Larix spp. from Russia: initial phase on the Russian-Scandinavian larch project. Eurasian Journal of Forest Research 4: 39–49.
Arima T., Maruyama N., Hayamura S., Nakamura N., Nanami N. (1993). Classification of log based on sound analysis and its application in product processing. Journal of the Society of Materials Science, Japan 42: 141–146. [In Japanese with English summary]. https://doi.org/10.2472/jsms.42.141.
Batkhuu N., Lee D.K., Tsogtbaatar J., Park Y.D. (2010). Seed quality of Siberian larch (Larix sibirica Ldb.) from geographically diverse seed sources in Mongolia. Scandinavian Journal of Forest Research 25(sup8): 101–108. https://doi.org/10.1080/02827581.2010.485815.
Cáceres C.B., Hernández R.E., Fortin Y. (2018). Variation in selected mechanical properties of Japanese larch (Larix kaempferi, [Lamb.] Carr.) progenies/provenances trials in Eastern Canada. European Journal of Wood and Wood Products 76(4): 1121–1128. https://doi.org/10.1007/s00107-018-1302-3.
Carter P., Briggs D., Ross R.J., Wang X. (2005). Acoustic testing to enhance western forest values and meet customer wood quality needs. In: Harrington C.A., Shoenholtz S.H. (eds.). Productivity of western forests: forest products focus. USDA, Forest Service, General Technical Report, Pacific Northwest Research Station, PNW-GTR-642 Portland, Oregon. p. 121–129.
Dulamsuren C., Hauck M., Leuschner H.H., Leuschner C. (2011). Climate response of tree-ring width in Larix sibirica growing in the drought-stressed forest-steppe ecotone of northern Mongolia. Annals of Forest Science 68(2): 275–282. https://doi.org/10.1007/s13595-011-0043-9.
Fedorkov A. (2014). Vitality and height growth of two Larix species and provenances in a field trial located in north-west Russia. Silva Fennica 48(1) article 1053. https://doi.org/10.14214/sf.1053.
Forest Study and Development Center, Ministry of Green Development and Tourism, Mongolia. (2016). Forest resource in Mongolia. Ulaanbaatar. p. 10–11. [In Mongolian].
Fukatsu E., Hiraoka Y., Matsunaga K., Tsubomura M., Nakada R. (2015). Genetic relationship between wood properties and growth traits in Larix kaempferi obtained a diallel mating test. Journal of Wood Science 61(1): 10–18. https://doi.org/10.1007/s10086-014-1436-9.
Gierlinger N., Jacques D., Schwanninger M., Wimmer R., Pâques L.E. (2004). Heartwood extractives and lignin content of different larch species (Larix sp.) and relationship to brown-rot decay-resistance. Trees 18(2): 230–236. https://doi.org/10.1007/s00468-003-0300-0.
Grabianowski M., Manley B., Walker J.C.F. (2006). Acoustic measurements on standing trees, logs and green lumber. Wood Science and Technology 40(3): 205–216. https://doi.org/10.1007/s00226-005-0038-5.
Ishiguri F., Matsui R., Iizuka K., Yokota S., Yoshizawa N. (2008). Prediction of the mechanical properties of lumber by stress-wave velocity and Pilodyn penetration of 36-year-old Japanese larch trees. Holz als Roh- und Werkstoff 66(4): 275–280. https://doi.org/10.1007/s00107-008-0251-7.
Karlman L., Mörling T., Martinsson O. (2005). Wood density, annual ring width and latewood content in Larch and Scots pine. Eurasian Journal of Forest Research 8: 91–96.
Koizumi A., Takada K., Ueda K., Katayose T. (1990). Radial growth and wood quality of plus trees of Japanese larch. I. Radial growth, density, and trunk modulus of elasticity of grafted clones. Mokuzai Gakkaishi 36: 98–102. [In Japanese with English summary].
Koizumi A., Kitagawa M., Hirai T. (2005). Effect of growth ring parameters on mechanical properties of Japanese larch (Larix kaempferi) from various provenances. Eurasian Journal of Forest Research 8: 85–90.
Koizumi A., Takata K., Yamashita K., Nakada R. (2003). Anatomical characteristics and mechanical properties of Larix sibirica grown in south-central Siberia. IAWA Journal 24(4): 355–370. https://doi.org/10.1163/22941932-90000341.
Kuz’mina N.A. (2004). Variation in parameters of Sibirian larch trees in different forest types in the Angara river basin. Russian Journal of Ecology 35(5): 303–307. https://doi.org/10.1023/B:RUSE.0000040683.10024.5e.
Lukkarinen A.J., Ruotsalainen S., Nikkanen T., Peltola H. (2009). The growth rhythm and height growth of seedlings of Sibirian (Larix sibirica Ledeb.) and Dahurian (Larix gmelinii Rupr.) larch provenances in greenhouse conditions. Silva Fennica 43(1): 5–20. https://doi.org/10.14214/sf.215.
Luostarinen K. (2011). Density, annual growth and proportions of types of wood of planted fast grown Siberian larch (Larix sibirica) trees. Baltic Forestry 17: 58–67.
Nagamitsu T., Nagasaka K., Yoshimaru H., Tsumura Y. (2014). Provenance tests for survival and growth of 50-year-old Japanese larch (Larix kaempferi) trees related to climatic conditions in central Japan. Tree Genetics & Genomes 10(1): 87–99. https://doi.org/10.1007/s11295-013-0666-0.
Nagao H., Washino K., Kato H., Tanaka T. (2003). Estimation of timber strength based on the distribution of MOE in the stem. Mokuzai Gakkaishi 49: 59–67. [In Japanese with English summary].
Neverov N.A., Belyaev V.V., Chistova Z.B., Kutinov Y.G., Staritsyn V.V., Polyakova E.V., Mineev A.L. (2017). Effects of geo-ecological conditions on larch wood variations in the North European part of Russia (Arkhangelsk region). Journal of Forest Science 63: 192–197. https://doi.org/10.17221/102/2015-JFS.
Park Y.S., Fowler D.P. (1983). A provenance test of Japanese larch in eastern Canada, including comparative data on European larch and tamarack. Silvae Genetica 32: 3–4.
Sobue N. (1986). Measurement of Young’s modulus by the transient longitudinal vibration of wooden beams using a fast Fourier transformation spectrum analyzer. Mokuzai Gakkaishi 32: 744–747.
Takata K., Hirakawa Y. (2000). Variation of the dynamic MOE in Japanese larch log by barking. Wood Industry 55: 352–356. [In Japanese with English summary].
Takada K., Koizumi A., Ueda K. (1992). Geographic variation in the moduli of elasticity of tree trunks among Japanese larch in provenance trial-stands. Mokuzai Gakkaishi 38: 222–227. [In Japanese with English summary].
Toda R., Mikami S. (1976). The provenance trials of Japanese larch established in Japan and the tentative achievements. Silvae Genetica 25: 5–6.
Tsehaye A., Buchanan A.H., Walker J.C.F. (2000). Sorting of logs using acoustics. Wood Science and Technology 34(4): 337–344. https://doi.org/10.1007/s002260000048.
Venäläinen M., Harju A.M., Terziev N., Laakso T., Saranpää P. (2006). Decay resistance, extractive content, and water sorption capacity of Siberian larch (Larix sibirica Ledeb.) heartwood timber. Holzforschung 60(1): 99–103. https://doi.org/10.1515/HF.2006.017.
Wang X., Carter P., Ross R.J. (2007) Acoustic evaluation of wood quality in standing trees. Part I. Acoustic wave behavior. Wood and Fiber Science 39: 28–38.
Wessels C.B., Malan F.S., Rypstra T. (2011). A review of measurement methods used on standing trees for prediction of some mechanical properties of timber. European Journal of Forest Research 130(6): 881–893. https://doi.org/10.1007/s10342-011-0484-6.
Zhu J., Nakano T., Tokumoto M., Takeda T. (2000). Variation of tensile strength with annual rings for lumber from the Japanese larch. Journal of Wood Science 46(4): 284–288. https://doi.org/10.1007/BF00766218.
Total of 32 references.

