Comparison of alternative roundwood pricing systems – a simulation approach
Malinen J., Haring M., Kilpeläinen H., Verkasalo E. (2015). Comparison of alternative roundwood pricing systems – a simulation approach. Silva Fennica vol. 49 no. 3 article id 1293. https://doi.org/10.14214/sf.1293
Highlights
- A discrete event simulation model was developed for studying roundwood pricing systems
- For a single buyer, pricing based on residual value appraisal produced (RVA) 4.87 per cent higher wood paying capability and 3.70 per cent higher stumpage price than pricing based on average unit prices
- As the number of buyers using RVA increases, the competition increased and the advantage decreased.
Abstract
In a closed market, roundwood buyers pricing system affect the roundwood flow from the stands to different roundwood users. If a buyer is capable to discriminate higher value stands from low quality stands better than its competitors, the buyer should be able to buy better raw material. In the study, a discrete event simulation was used to examine the effect of residual value appraisal (RVA) -based pricing of roundwood by log dimensions and grades compared to the traditional pricing based on average unit prices (UP) of roundwood assortments on roundwood flow. The core of the simulation model was the data containing 51 pine dominated stands from southern Finland. Sample trees were theoretically bucked by the bucking simulator in order to estimate the volumes, dimensions and grades of the logs and roundwood assortments. The simulation model of roundwood markets included four roundwood buyers, two corporations and two saw milling enterprises. The main finding of the study was that the buyers who use RVA gains an advantage and receives better quality compared to buyers who use UP. As the number of buyers using RVA increases, the competition increased and the advantage decreased.
Keywords
simulation;
pricing;
roundwood
-
Malinen,
University of Eastern Finland, School of Forest Sciences, P.O. Box 111, FI-80101 Joensuu, Finland
E-mail
jukka.malinen@uef.fi

- Haring, University of Eastern Finland, School of Forest Sciences, P.O. Box 111, FI-80101 Joensuu, Finland E-mail mika.haring@gmail.com
- Kilpeläinen, Natural Resources Institute Finland (Luke), Bio-based business and industry, P.O. Box 68, FI-80101 Joensuu, Finland E-mail harri.kilpelainen@luke.fi
- Verkasalo, Natural Resources Institute Finland (Luke), Bio-based business and industry, P.O. Box 68, FI-80101 Joensuu, Finland E-mail erkki.verkasalo@luke.fi
Received 16 December 2014 Accepted 8 May 2015 Published 4 June 2015
Views 88898
Available at https://doi.org/10.14214/sf.1293 | Download PDF

1 Introduction
The pricing of roundwood is most typically based on unit prices for different roundwood assortments, which are negotiated between the buyer and the seller. Instead of strict cost accounting, the levels of prices of industrial roundwood are usually based on market price levels transacted in particular countries or regions (Suchomel et al. 2012). The regional price levels depend on supply of and demand for tree species, roundwood assortments and qualities. Global markets of the products or the changes in end use demand affect the volume of demand of roundwood in different regions.
Due to the variation in the value of roundwood assortments at production by log dimensions and grades, other pricing systems based on roundwood assortments and log dimensions are also used (Puumarkkinoiden toimintaa… 2009; Malinen et al. 2010). In these systems, some roundwood assortments may be priced by using unit price per unit volume, but certain assortments are priced using a different price for each log length and diameter according estimated end-use value. It is also possible to divide roundwood assortments into grades, that is, the price of the log depends on the roundwood assortment, volume, grade and log length-diameter class. This kind of pricing systems are more common for example in Sweden, where pine saw logs has four grade classes and spruce two, and price varies also according to dimensions of logs (Puumarkkinoiden toimintaa… 2009).
According to Adams and Haynes (1991), the residual value appraisal (RVA) has been a common pricing system used for the roundwood of the U.S. National Forest Service where the price is the residual left after deducting all costs and profit expectation from the expected selling value of products made from that roundwood. The residual appraisal value has an analogy to wood paying capability (WPC), which is considered a maximum tolerated price that can be paid for the wood raw material after all costs (excluding wood) have been reduced from the sale price of the products (Jylhä et al. 2010).
Malinen and Kilpeläinen (2013) studied the relationships between the pricing of roundwood and the end use value applying different pricing systems. The results indicated that the pricing based on residual values of log dimensions and grades had clear advantages compared to the other pricing systems. The stumpage values were divided more by the WPC when applying the pricing based on log dimensions, whereas the other pricing systems produced more or less excessive stumpage value for the stands where the WPC was low, and low stumpage values for the stands where the WPC was high.
Although the RVA based pricing has advantages, possibilities to determine the WPC depend on the roundwood trading mechanism and the end products. For saw logs, the WPC can be accounted fairly easily from the sawn products and side products, such as bark, chips and sawdust. For pulpwood, determination of the WPC is usually based on the average costs, total wood consumption and the sale income from pulp, energy and by-products (Diesen 2007), and therefore, variation of the WPC from different raw material sources is difficult to determine. In general, as the complexity of end product increases, the more difficult it is to determine the WPC.
The trading mechanism affects also to the pricing system used in roundwood markets. The amount, dimensions and grades are usually more easily and accurately measured from the harvested tree stock than from standing trees. Consequently, pricing systems based on unit prices of assortment are more typical in countries where standing sales are dominant, such as France, where 80% of volume is sold by standing sales (Puumarkkinoiden toimintaa… 2009), and Finland, where 89% of the volume purchased from privately owned forest is sold by standing sales (Finnish Statistical… 2013). However, when utilising cut-to-length harvesting, harvesters are able to measure and save the length-diameter distribution of the logs by roundwood assortments and grades, and technical obstacles for the use of RVA based pricing does not exist.
Although non-monetary values, such as reliability, resilience, aesthetic values and biodiversity, have a role for a segment of non-industrial private forest (NIPF) owners (Sikanen 1999; Häyrinen et al. 2014), the monetary goals are most often decisive in selling roundwood. In forest economics, irrespective of the forest owner’s preferences and consumption plans, it is assumed that the decision-maker will maximise the net present value of harvest revenue (Amacher et al. 2009). It includes rational behaviour when choosing the roundwood buyer; the roundwood is sold to the buyer whose buying bid is the highest. Accordingly, if a roundwood buyer is able and willing to utilise RVA based pricing and discriminate high quality stands from low quality stands, the buyer will obtain higher quality raw material. In a short-term closed roundwood market, if someone is obtaining better quality as before, the others will have to settle for lower quality.
In a long-term, price premiums and discounts communicate and prompt the changes needed in production to the producers. Within the limitations of a growing site, the forest owners are able to consider the economic feasibility of different actions, such as species selection for forest regeneration, silvicultural treatments of the stand, and possible investments, such as fertilising or pruning, as well as rotation period. Hence, from the forest owner’s point of view, it is important that the price level and pricing system of roundwood reflect the value of the raw material in the potential end uses, providing incentives to grow raw material which has the greatest added value in further processing and products.
Although incorrect price and/or quality information can lead to distortion in the market and to market inefficiency (Hudson et al. 1998), the pricing strategies taking account the heterogeneity of roundwood raw material has attracted surprisingly little public interest considering the importance of the matter. Research into the roundwood trade has concentrated on econometric analyses on roundwood markets and market prices (e.g. Mutanen and Toppinen 2007), the objectives of NIPF owners (e.g. Häyrinen et al. 2014), and the management of the roundwood procurement process (e.g. Helstad 2006).
Tolvanen-Sikanen et al. (1995) studied the effects of the probability of the roundwood buyer’s awareness, the probability of the seller’s willingness to sell, the buyer’s wood paying capability, and the grade class distribution of pine logs utilising simulation of roundwood flows. The main focus of the study was to model two theories of decision-making in the roundwood procurement process; willingness to sell and buyer’s awareness. The pricing systems were not considered.
Malinen and Kilpeläinen (2013) studied the relationships between the pricing of roundwood using different pricing systems and the end use value. According to the results, RVA based pricing by log dimensions and grades did produce better price transmission between end-product and stumpage value, but purchasing competition and the effect on timber flow were not considered. From the viewpoint of the buyer utilising RVA based pricing the question in a short-term closed market is how much higher the overall quality considered by WPC would be and how much higher the stumpage price will become. The buyer’s decisions to utilise RVA based pricing affect the other buyers’ timber flow as well. Moreover, if several buyers are utilising the RVA based pricing, what are the effects on the timber flow?
The main objective of the study was to examine the effect of residual value appraisal (RVA) based pricing of roundwood by log dimensions and grades compared to the traditional pricing based on average unit prices (UP) of roundwood assortments on roundwood flow. For this purpose, a discrete event simulation model applying contract theory was constructed and validated. The developed simulation model included four different roundwood buyers, two of them being corporations buying roundwood for sawmilling and pulping, and two of them being sawmills buying roundwood just for sawmilling. By using the developed simulation model, the suitability of achieved roundwood raw material by each type of roundwood buyer and different combinations of pricing scenarios was evaluated by using wood paying capability (WPC), that is, a residual value at the stump, as an indicator of the suitability of the roundwood raw material from the stand to the selected production. Furthermore, the influence of different pricing scenarios on hauling distances was evaluated.
2 Material and methods
2.1 Implementation of the simulation model
As the aim of the study was to investigate the effect of a pricing system on roundwood flow at a general level, the simulation model was purposely developed to be as uncomplicated as possible. The following principles were set as a prerequisite:
- Stands on the market have to be realistic in terms of Finnish conditions
- Roundwood buyers have to have realistic in terms of wood usage
- The price of the roundwood has to be feasible, considering the costs and revenue related to roundwood raw material
- When the levels of recovery of the roundwood assortments by the roundwood buyer are lower than the demand, the offered price rises
- When the levels of recovery of the roundwood assortment by the roundwood buyer are greater than the demand, the offered price falls.
The models were determined theoretically and the parameters were adjusted heuristically utilising dynamic face validation (Sargent 2011). As real life includes uncertainty and randomness, the model includes elements of randomness in terms of the location and size of the marked stands, and the buyer’s willingness to produce a bid.
The roundwood procurement model is a discrete event dynamic simulation model, where at each stage a group of marked stands enters the market, and the roundwood buyers face the same market stage (Fig. 1). For each marked stand, each buyer decides whether to make a bid and what the price of that bid is. The seller selects the highest bid, and the roundwood traded is updated in the roundwood buyers’ accumulation and, if the total amount of roundwood procured is not achieved, a new stage begins.
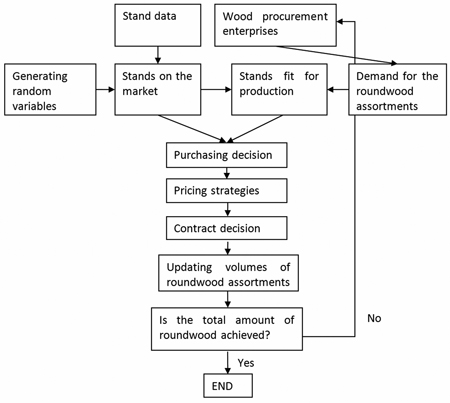
Fig. 1. The main parts of the roundwood procurement model.
The core of the simulation model is the data containing 51 timber stands from southern Finland. The study data was collected by measuring 577 standing Scots pine (Pinus sylvestris L.) sample trees from pine-dominated study stands. Each tree was measured for its dimensions and assessed for stem quality. In the roundwood procurement simulation model, the stand data per hectare of Scots pine remains unchanged (Table 1). However, in each case the coordinates and area varies in each stage event.
| Table 1. The main characteristics of the Scots pine timber stands in the simulation model. Dgm is the basal area median diameter at breast height and Hgm is the height of the respective tree. | ||||
| Variable | Random | Min | Max | Average |
| x and y coordinates of the stand (m) | Yes | 0 | 150 000 | |
| Area (ha) | Yes | 0.5 | 5 | |
| Volume (m3/ha) | No | 86.1 | 355.5 | 181.2 |
| Dgm (cm) | No | 23.4 | 33.3 | 28.4 |
| Hgm (m) | No | 17.0 | 29.0 | 23.3 |
| Share of grade A butt logs (%) | No | 1.6 | 39.4 | 25.8 |
| Share of conventional saw los (%) | No | 26.9 | 62.5 | 47.3 |
| Share of small-diameter saw logs (%) | No | 0.9 | 12.9 | 4.8 |
| Share of pulpwood (%) | No | 6.6 | 48.5 | 20.6 |
All pines from the sample plots were theoretically bucked by the bucking simulator based on the bucking-to-value approach and dynamic programming. Bucking simulations were used in order to estimate the volumes of different roundwood assortments, length-diameter distributions, grade and value of the logs.
Based on the length-diameter distributions of the different roundwood assortments, the wood paying capability (WPC) at the stump were calculated by reducing roundwood procurement costs from the residual values at the production plants according to average roundwood procurement costs (Finnish Statistical… 2013). For the pulpwood, estimation of the WPC was based on estimation of average costs, total wood consumption and the sale income from pulp, energy and by-products excluding capital costs of pulp manufacturing (Diesen 2007), leading to constant WPC 40 €/m3 at the mill for all pulpwood. Roundwood harvesting costs were 8.16 €/m3 for saw logs and 16.77 €/m3 for pulpwood. For all roundwood assortments, hauling costs were 7.4 cents/m3/km and general management overhead costs were 2.79 €/m3. For a more detailed description of the data and value calculations, see Malinen and Kilpeläinen (2013).
The roundwood procurement simulation model includes four roundwood buyers, from which two are big corporations utilising different grades and sizes of saw logs in saw milling and pulpwood in pulp production. Two roundwood buyers are saw milling enterprises using different grades and dimensions of saw logs in their production, but selling pulpwood to one of the two corporations according to which one of them is closer to the stand (Table 2). In the simulation model, the roundwood procurement objectives have been defined as an annual objective for the roundwood procurement area, not for the production. Therefore, the amount purchased does not fulfil the total demand for the production, especially in the case of pulpwood procurement.
| Table 2. Roundwood procurement objectives (m3) of the roundwood buyers. | |||||
| Corporation, buyer A | Corporation, buyer B | Sawmill, buyer C | Sawmill, buyer D | Total | |
| Grade A butt logs | 198 000 | 153 600 | 40 800 | 129 200 | 521 600 |
| Conventional saw logs | 423 000 | 275 200 | 70 200 | 193 800 | 964 000 |
| Small-diameter logs | 45 000 | 25 600 | 7200 | 17 000 | 94 800 |
| Pulpwood | 234 000 | 185 600 | 419 600 | ||
| Total | 900 000 | 640 000 | 120 000 | 340 000 | 2 000 000 |
Both corporations using roundwood in sawing and pulp production have two production units in the procurement area, a sawmill and a pulp mill. For Corporation A these plants are located at the same site. For Corporation B, the sawmill and the pulp production unit are in different locations. Sawmills C and D both have only one production unit (Fig. 2).
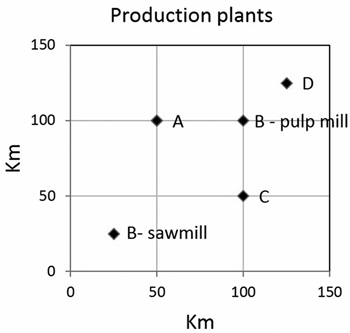
Fig. 2. The locations of the production plants. Corporation A has both a sawmill and a pulp mill at the same address, Corporation B has sawmill (B-sawmill) and pulp production unit (B-pulp plant) in different locations, and Sawmills C and D both have only one sawmill.
When purchasing roundwood from standing sales, the interest of roundwood buyers in marked stands depends on the demand for potential roundwood assortments. In the simulation model, for each roundwood buyer, both the relative share of the acquired roundwood compared to total roundwood bought from the area and the relative share of each roundwood assortment is known. The relative share of roundwood assortment (Sij) is defined as:
where
VRij = recovery of roundwood assortment j in roundwood buyer i
VDij = demand of roundwood assortment j in roundwood buyer i
If the recovery of roundwood assortment (VRij) is 0, also the relative share (Sij) is 0. If the recovery of assortment equals to demand (VDij), the relative share is 1. If the recovery is twice or more as much as demand, the Sij is 2. The value of (Sij) was restricted to 2 in order to restrict negative values in Eq. 2. The relative share of the roundwood assortment is used in the calculation of the coefficient of the demand of roundwood assortment (DCij):
The DCij is 0if the share of roundwood assortment is double or more than the demanded share, and the DCij is 1 if the share of the roundwood assortment is zero. The best fit for the production of the roundwood assortment recovery is when the share of each roundwood assortment is the same as the demand. Therefore, the fit for production of the roundwood for the roundwood buyer i from the marked stands k (FPik) is defined as:
![]()
where
VRjk = volume recovery of roundwood assortment j in stand k
The fit for production (FPik) defines the suitability of marked stand k for the buyer i at the stage. The fit for production is dependent on the accumulation of roundwood assortments compared to share of roundwood assortment in the procurement area at given stage. Thus, the buyer may have shortage or surplus of roundwood assortment unconnected to other roundwood assortments. High values of FPik in a stand indicates high proportions of roundwood assortments which buyer i has shortage.
The purchasing decision of the roundwood from a stand is dependent on the hauling distance from the stand to the production plant, the fit for production of the roundwood assortments and the seller-buyer relationship. They all influence the buyer’s awareness of and interest in buying the roundwood from the stand. The buyers are not aware of other buyers’ actions. In the roundwood procurement simulation model, the main interest was to analyse roundwood flows when alternative pricing systems were used and the social elements such as the seller-buyer relationship was left out on purpose. Therefore, the decision to purchase roundwood from the stand was depicted by the hauling distance from the stand to production, the fit for production and the random element depicting the inefficiency of roundwood markets.
The rate for the willingness to purchase roundwood (WPik) is calculated as:
where
DPijk = volume weighted average distance between the stand k and the production plant for the roundwood assortment j for the roundwood buyer i.
If the WPik for the roundwood buyer i and stand k is greater than the random element (random number scaled between 0and 1), the roundwood buyer will make a purchasing bid for the stand k.
The pricing strategy is adapted from Tolvanen-Sikanen et al. (1995), where game theory pattern of thinking of closed offers in a simultaneous game was used. The price (Pijk) offered from the roundwood assortment from the stand is adapted according Wood Paying Capability (WPC) and pricing strategy coefficient (Sijk):
In the pricing strategy, the roundwood buyer usually prefers the stands near their mills, and the offered price will be higher. In addition, the better the fit is between production demand and roundwood assortments from the stand, the higher the price. Similarly, tougher competition, that is the greater number of the simultaneous buyers, leads to a higher price. The pricing strategy coefficient (Sijk) is:
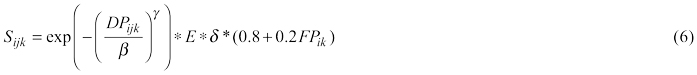
where
β γ = constants defined heuristically
E = coefficient describing the buyer’s profit expectation
δ = effect of competition
In the simulation, the values for the constants β γ were set to 450 and 2.5, respectively. The gross margin at the stump was set to 10% for pulpwood and saw logs, 5% for small-diameter saw logs and 25% for grade A butt logs. Note that the gross margin includes the whole value added chain, although the profit is calculated against all costs at production. The effect of competition δ is:
where
nb = number of roundwood buyers
A roundwood buyer wins the closed offer competition if the offered total price is the highest of all the buyers’ offers. Sawmills C and D do not use pulpwood and therefore the pulpwood bought by C and D will be sold to corporation A or B depending on which one’s pulp mill is closest to the stand. The price paid for the pulpwood by sawmill C or D to the forest owner is the price offered. The price paid by corporation A or B to sawmill C or D is the price which corporation A or B would have been willing to pay regardless of whether the corporation made a purchasing bid or not. As a result, if the price acquired by the sawmill from the corporation is bigger than the price paid to the forest owner, the sawmill makes a profit from the transaction. And vice versa, if the price gained by the sawmill from the corporation is smaller than the price paid to the forest owner, the sawmill will lose money.
At the end of each stage, the amounts of purchased roundwood assortments are added to the yearly accumulation of roundwood assortments. The simulation continues until the cumulative objective of the roundwood buyers is met (Table 2).
2.2 Validation of the model
The model and parameters used in the model were tested by sensitivity analysis in order to ensure the intended operation of the model. For the validation, total harvesting recoveries, roundwood procurement objectives and locations of the productions plants were altered. A total of 400 simulation schemes were run. In the validation, the pricing of the roundwood assortment for all roundwood buyers was based on the same average unit prices. Therefore, the only differences between the WPCs of the roundwood buyers resulted from the hauling distance between the marked stand and the production plant.
The most important objective in the validation was to ensure necessary competition between roundwood buyers in each market scenario and to ensure that the roundwood buyers make appropriate adjustments to the price levels if their roundwood assortment accumulations are too low or too high; that is, that they adjust the price level that ensures the availability of raw material as efficiently as possible without paying excessive prices for roundwood.
2.3 Roundwood pricing systems and pricing scenarios
In the pricing based on unit prices of roundwood assortments (UP), each roundwood assortment has one unit price which is based on the average WPC of roundwood assortment in the procurement area and the pricing strategy. In the pricing based on residual value appraisal (RVA), the price of roundwood is based on WPCs of different assortments, grades and dimensions, and the pricing strategy. The wood end use value for the pulpwood has one constant value.
In the basic pricing scenario (S1), each roundwood buyer uses UP as a pricing system (Table 3). In the second case of pricing scenarios (S2-S5), each roundwood buyer, in turn, uses RVA as a pricing system while other buyers stay in UP. In the third case (S6-S15), each RVA roundwood buyer is facing competition, thus also other buyers utilise RVA and in the end, all roundwood buyers are using RVA (S16).
| Table 3. Pricing scenarios (S1-S16) in the study. The default pricing system is based on unit prices of roundwood assortment (UV), the pricing based on residual value appraisal (RVA) is marked with an “X”. | ||||||||||||||||
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | S11 | S12 | S13 | S14 | S15 | S16 | |
| Buyer A | X | X | X | X | X | X | X | X | ||||||||
| Buyer B | X | X | X | X | X | X | X | X | ||||||||
| Buyer C | X | X | X | X | X | X | X | X | ||||||||
| Buyer D | X | X | X | X | X | X | X | X | ||||||||
3 Results
3.1 Model validity
In the validation, the average number of buying bids for each marked stand was 3.74. In 28 cases out of the total of 408 000 stands on the market, none of the buyers made a buying offer of the roundwood from the marked stand. The unit stumpage values (USV) paid from the saw logs to the forest owners were at the same level as the average USV in South-East Finland 1/2011–7/2014 (Table 4), when the USV for roundwood from clear-cutting areas were 57.27 €/m3 (Metinfo 2014). The USV in South-East Finland was higher for the small-diameter saw logs (24.28 €/m3) and pulpwood (17.24 €/m3) than the average USV in the simulations, and considerably higher than the minimum USV in the simulations. This was caused by the long hauling distances in some validation schemes, which pushed the USV to unrealistically low levels. Statistics for the specific prices of the grade A butt log were not available, as they are included in the prices of saw logs.
| Table 4. Average residual values (€/m3) at the production and wood paying capabilities (WPC) (€/m3) at the stump, and the maximum, average and minimum unit stumpage values (USV) (€/m3) for the roundwood assortments in the validation simulations. | ||||
| Grade A butt logs | Saw logs | Small-diameter saw logs | Pulpwood | |
| Average residual value at production | 112.78 | 81.62 | 38.62 | 40.00 |
| Average WPC at the stump | 97.34 | 66.10 | 23.11 | 18.46 |
| Max USV | 71.94 | 59.79 | 24.71 | 19.64 |
| Average USV | 66.74 | 54.32 | 20.12 | 15.17 |
| Min USV | 44.61 | 33.45 | 6.04 | 6.60 |
3.2 The effect of RVA-based pricing on roundwood flow
In the basic pricing scenario (S1), each roundwood buyer uses pricing based on UP and has the same residual values at the production. The differences in the WPCs of different buyers are based on the locations of the production plants, which defines the hauling distances and the competition that buyers are facing (Table 5). The USVs are also affected by the roundwood procurement objectives.
| Table 5. Wood paying capability (WPC) and unit stumpage value (USV) as euros per cubic metre in the basic pricing scenario (S1), where each roundwood buyer uses pricing based on unit prices (UP) of roundwood assortments. | |||||
| Grade A butt logs | Saw logs | Small-diameter saw logs | Pulpwood | All assortments | |
| WPC/USV | WPC/USV | WPC/USV | WPC/USV | WPC/USV | |
| Buyer A | 99.97 / 68.50 | 67.45 / 56.01 | 24.48 / 21.23 | 19.55 / 16.32 | 63.43 / 49.03 |
| Buyer B | 100.04 / 68.08 | 67.33 / 55.63 | 24.32 / 21.04 | 16.59 / 13.30 | 53.81 / 41.29 |
| Buyer C | 99.70 / 63.65 | 67.58 / 52.12 | 25.2 / 20.08 | 75.12 / 53.55 | |
| Buyer D | 100.50 / 67.26 | 67.79 / 54.88 | 25.02 / 21.03 | 76.48 / 57.31 | |
In the pricing scenarios S2-S5 each roundwood buyer, in turn, adopted the RVA pricing (Table 6). The average WPC, which reflects the overall suitability of the roundwood assortments for production, increased from 1.58 per cent (buyer A) to 4.87 per cent (buyer C), and USV increased to 1.75 and 3.70 per cent, respectively. However, the absolute increase in USV was smaller in each case than the increase in WPC. The increase in the WPC was the highest for the roundwood buyer whose initial WPC was lower than that of the corresponding roundwood buyers.
| Table 6. The change in wood paying capability (WPC) and unit stumpage value (USV) in euros per cubic metre compared to basic scenario S1 (Table 5) for scenarios S2-S5 where each buyer in turn uses residual value appraisal (RVA)-based pricing and other buyers use pricing based on the unit prices (UP) of roundwood assortments. | |||||
| Grade A butt logs | Saw logs | Small-diameter saw logs | Pulpwood | All assortments | |
| WPC/USV | WPC/USV | WPC/USV | WPC/USV | WPC/USV | |
| Buyer A uses RVA, other buyers use UP: | |||||
| Buyer A | 1.31 / 1.77 | 0.53 / 0.48 | -0.16 / 0.16 | -0.58 / -0.54 | 1.00 / 0.86 |
| Buyer B | -1.63 / 0.29 | -0.82 / 0.23 | -0.06 / -0.01 | 0.05 / 0.06 | -1.27 / -0.21 |
| Buyer C | -1.32 / 0.45 | -0.72 / 0.34 | 0.02 / 0.13 | -1.21 / 0.17 | |
| Buyer D | -1.45 / 0.33 | -0.82 / 0.23 | -0.07 / -0.03 | -1.70 / -0.17 | |
| Buyer B uses RVA, other buyers use UP: | |||||
| Buyer A | -1.01 / 0.06 | -0.54 / 0.03 | -0.06 / -0.11 | -0.03 / -0.02 | -0.91 / -0.20 |
| Buyer B | 1.34 / 2.01 | 0.62 / 0.61 | -0.20 / 0.10 | 0.15 / 0.11 | 1.90 / 1.60 |
| Buyer C | -1.72 / 0.44 | -0.91 / 0.30 | -0.09 / 0.04 | -1.61 / 0.07 | |
| Buyer D | -0.12 / 0.25 | -0.05 / 0.21 | 0.07 / 0.05 | -0.18 / 0.17 | |
| Buyer C uses RVA, other buyers use UP: | |||||
| Buyer A | -0.18 / 0.00 | -0.13 / 0.00 | 0.03 / -0.04 | 0.02 / 0.02 | -0.14 / -0.03 |
| Buyer B | -0.77 / -0.11 | -0.47 / -0.12 | -0.31 / -0.29 | 0.01 / 0.08 | -0.69 / -0.29 |
| Buyer C | 3.34 / 2.00 | 1.92 / 0.92 | -0.38 / 0.02 | 3.66 / 1.98 | |
| Buyer D | -0.50 / -0.14 | -0.35 / -0.15 | -0.17 / -0.22 | -0.53 / -0.25 | |
| Buyer D uses RVA, other buyers use UP: | |||||
| Buyer A | -0.74 / -0.02 | -0.39 / -0.04 | -0.07 / -0.12 | 0.00 / 0.00 | -0.69 / -0.22 |
| Buyer B | -0.17 / 0.10 | -0.06 / 0.08 | -0.02 / -0.01 | 0.06 / 0.08 | -0.63 / -0.34 |
| Buyer C | -1.29 / 0.14 | -0.66 / 0.06 | -0.14 / -0.06 | -1.21 / -0.12 | |
| Buyer D | 1.34 / 1.67 | 0.63 / 0.34 | -0.17 / 0.20 | 1.76 / 1.27 | |
In the competition, the buyer who uses RVA gains an advantage and receives better quality compared to buyers who use UP (Fig. 3). As the number of buyers using RVA increases, the competition increases and the advantage decreases, and if all buyers use RVA, the advantage is lost and the value of the achieved raw material is the same as it is when using UP.
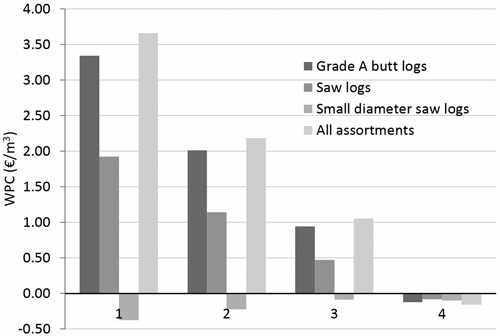
Fig. 3. The effect of competition on the WPC (€/m3) of roundwood buyer C when it is the only user of residual value appraisal (RVA)-based pricing (1), one other buyer is also using RVA (2), two other buyers are using RVA (3) or all buyers are using RVA (4).
In the basic scenario (S1), the location of the production plants is the key variable affecting who is capable of paying the highest price for the stand. As the importance of the roundwood suitability for production increases, the hauling distances grow (Fig. 4). The scenario where one half of the roundwood buyers are using UP and the other half are using RVA results in the longest hauling distances. However, if all buyers have similar preferences in terms of roundwood quality (S16), the setting is the same as in the basic scenario.
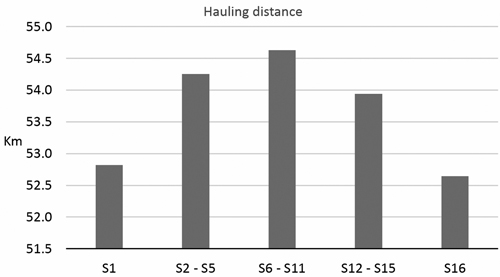
Fig. 4. The effect of competition on hauling distance, when all buyers use UP (S1), only one buyer uses residual value appraisal (RVA) (S2 – S5), two buyers use RVA (S6 – S11), three buyers use RVA (S12 – S15) or all buyers use RVA.
4 Discussion
In this study, a discrete event simulation was used to investigate the roundwood flow when using two different pricing systems in roundwood procurement. The model developed in the study follows the basic principle of the buying process presented by Tolvanen-Sikanen (1995). The stands are sold exclusively to one buyer. Only pulpwood is sold forward if the buyer is an independent sawmill. There are no trade-off to balance roundwood accumulation and the roundwood catchment area is closed. Both limitations emphasise the suitability of the roundwood in a stand in terms of production and highlight the effects of roundwood pricing.
In general, the selected approach of a discrete event simulation and interactive decision making between the forest enterprises, which is fundamentally and in its spirit closely connected to the concept of stage games in game theory, performed logically. In the sensitivity analysis, the minimum unit price of pulpwood and small-diameter saw logs were in some cases unrealistically low. Although this does not affect the results of the study, a lower limit for the minimum price should be added to the simulator. One other consideration is the amount of stands entering the market at each stage. In the study, all 51 stands were included in each stage. If a buyer had a shortage of roundwood, it reflected on all 51 bids.
According to the results of the study, the roundwood buyer that applies the pricing system based on residual value appraisal (RVA) benefits from better raw material than the buyers who apply the pricing system based on constant unit prices (UP). Although the stumpage price is then higher than average, the absolute value increment of raw material is greater in all cases. Increasing competition reduces the advantage, and in the scenario when all buyers utilise RVA, the advantage vanishes. The long-term benefits still remain, as the price premiums encourage roundwood sellers to produce higher quality raw material.
In the real roundwood purchasing process, choosing the roundwood buyer by NIPF owners is complicated by a multitude of factors such as long-term seller-buyer relationships and environmental aspects (Sikanen 1999; Häyrinen et al. 2014). None of these is contradictory to the results on the effects of different pricing systems; therefore, the tendencies of the results in the study can be considered reasonably reliable.
In the study, the end use values of roundwood assortments, log dimensions and grades were assumed to be the same for the roundwood end users considered. However, there is variance in the end use values of individual logs within the same roundwood assortment and dimensions. Some part of the variation can be attributed to the external properties of logs, but external visual grading is not necessarily in accordance with the real values of the sawn timber produced (Chiorescu and Grönlund 2003). Moreover, automatic grading has been found to be less accurate than manual grading, for example in the test set consisting of Scots pine and Norway spruce logs from five sawmills in different parts of Sweden (Enlund 2004).
The pricing of roundwood depends largely on the sale type. In the case of delivery sales, it is easier to assess the external quality of the logs and the value the roundwood accordingly. In the case of standing sales, the quantity and the quality of the standing stock cannot be assessed so exactly before harvesting as in the case of delivery sales. According to Larson and Hardie (1989), standing sales takes place in a market where information about quantity, quality and value of the product is costly to obtain. As the methods of forest inventory develop, it may be easier and more accurate to estimate the recovery of roundwood assortments and grades (e.g. Maltamo et al. 2009; Barth & Holmgren 2013; Vauhkonen et al. 2014).
The current study was based on simplified assumptions of the roundwood trade. In the future, the simulation model should be expanded to include different product profiles with specialised production and different residual values, exchange of all roundwood assortments between buyers, the possibility to utilise one’s own forests to balance the accumulation and include different roundwood seller profiles. By utilising the updated simulation model, the performance of new pricing systems, such as pricing by stem fractions, could be analysed.
In conclusion, in the short-term the quality of roundwood raw material in the market is constant. The pricing system only affects the distribution of the different log dimensions and grades between different roundwood buyers. Assuming that the end use value of the raw material is more or less the same between different roundwood end users, the pricing system is irrelevant if all buyers are pricing raw material in the same manner. However, in the long-term, the pricing system has a large impact on the roundwood assortments and qualities, and even on the species to be grown and entering the market. This, however, does not seem to concern roundwood buyers whose business success is estimated by annual quarters. Nevertheless, since there are no visible extra costs from roundwood pricing based on residual value appraisal, the first buyers entering the market to do so will also benefit in the short-term. “A clever forester earns more money than a mainstream one – and should do so” (Gjerdrum 2008).
Acknowledgements
This work was mainly conducted as part of the research project of the Finnish Forest Research Institute’s “Assessing quantity, quality and value of wood raw material for timber trade and procurement”. The foundations for the work were developed in the European Union Northern Periphery Programme funded project “Development of Scots Pine Resource”. The authors acknowledge the help and support of all the partners in the projects and thank three anonymous reviewers for their constructive comments.
References
Adams D.M., Haynes R.W. (1991). National forest timber supply and stumpage markets in the western United States. Pacific Northwest Research Station, Forest Service, United States Department of Agriculture. Research Paper PNW-RP-435. 55 p.
Amacher G.S., Ollikainen M., Koskela E. (2009). Economics of forest resources. The MIT press, Cambridge MA, U.S. 397 p.
Barth A., Holmgren J. (2013). Stem taper estimates based on airborne laser scanning and cut-to-length harvester measurements for pre-harvest planning. International Journal of Forest Engineering 24(3): 161–169. http://dx.doi.org/10.1080/14942119.2013.858911.
Chiorescu S., Grönlund A. (2003). The visual grading system for Scots pine logs in relation to the quality of sideboards produced. Forest Products Journal 53: 53–60. .
Diesen M. (2007). Economics of the pulp and paper industry. Second edition. Paperi ja Puu Oy, Helsinki. 222 p.
Enlund J. (2004). Automatic grading of softwood sawlogs for pricing using external geometry. Scandinavian Journal of Forest Research 19: 38–47. http://dx.doi.org/10.1080/02827580410017834.
Finnish Statistical Yearbook of Forestry. (2013). Finnish Forest Research Institute. 450 p. ISBN 978-951-40-2450-4.
Gjerdrum P. (2008). Reflections over the multifaceted significance of timber prices – based on the Scandinavian practice. In: Teischinger A. (ed.). Wood quality and niche products. Proceedings of the COST Action E40 conference. Lignavosionen 19. 80 p.
Häyrinen L., Mattila O., Berghäll S., Toppinen A. (2014). Changing objectives of non-industrial private forest ownership: a confirmatory approach to measurement model testing. Canadian Journal of Forest Research 44(4): 290–300. http://dx.doi.org/10.1139/cjfr-2013-0211.
Helstad K. (2006). Managing timber procurement in Nordic purchasing sawmills. Acta Wexionensia 93/2006. 59 p. ISBN: 91-7636-508-5.
Hudson D., Ethridge D., Segarra E. (1998). Incorrect price information for a heterogeneous commodity: a conceptual synthesis. Review of Agricultural Economics 20(2): 365–376. http://dx.doi.org/10.2307/1349995.
Jylhä P., Dahl O., Laitila J., Kärhä K. (2010). The effect of supply system on the wood paying capability of kraft pulp mill using Scots pine harvested from first thinnings. Silva Fennica 44(4): 695–714. http://dx.doi.org/10.14214/sf.454.
Larson D.M. I.W. Hardie. (1989). Seller behavior in stumpage markets with imperfect information. Land Economics 3: 239–253.
Malinen J., Kilpeläinen H. (2013). Price systems for standing sales of industrial roundwood in Finland. Baltic Forestry 19(2): 307–315.
Malinen J., Berg V., Kilpeläinen H. (2010). Roundwood pricing mechanisms and their performance in Scots pine roundwood markets. Metlan työraportteja/Working Papers of the Finnish Forest Research Institute 174. 35 p. http://www.metla.fi/julkaisut/workingpapers/2010/mwp174.htm.
Maltamo M., Peuhkurinen J., Malinen J., Vauhkonen J., Packalén P., Tokola T. (2009). Predicting tree attributes and quality characteristics of Scots pine using airborne laser scanning data. Silva Fennica 43(3): 507–521. http://dx.doi.org/10.14214/sf.203.
MetINFO – Forest information services. (2014). Forest-related information services and expert systems. Finnish Forest Research Institute. http://www.metla.fi/metinfo/index-en.htm. [Cited 10 September 2014].
Mutanen A., Toppinen A. (2007). Price dynamics in the Russian-Finnish roundwood trade. Scandinavian Journal of Forest Research 22(1): 71–80. http://dx.doi.org/10.1080/02827580601138207.
Puumarkkinoiden toimintaa koskeva selvitys. (2009). Työ ja elinkeinoministeriö. [Final report of investigation of roundwood trade by the ministry of employment and economy]. Pöyry Forest Industry Consulting Oy. 84 p. [In Finnish]. https://www.tem.fi/files/25627/tem_68_2009_web.pdf.
Sargent R.G. (2011). Verification and validation of simulation models. In: Jain S., Creasey R.R., Himmelspach J., White K.P, Fu M. (eds.). Proceedings of the 2011 Winter Simulation Conference. p. 183–198. http://dx.doi.org/10.1109/WSC.2011.6147750.
Sikanen L. (1999). Discrete event simulation model for purchasing process of marked stands as a part of customised timber procurement in Finland. Faculty of Forestry, University of Joensuu. Research Notes 95. 47 p.
Suchomel J., Gejdoš M., Amprušová L., Šulek R. (2012). Analysis of price changes of selected roundwood assortments in some Central Europe countries. Journal of Forest Science (11): 483–491.
Tolvanen-Sikanen T., Sikanen L., Harstela P. (1995). A game theoretic simulation model for quality oriented timber supply to sawmills. Silva Fennica 29(1):71–86. http://dx.doi.org/10.14214/sf.a9198.
Vauhkonen J., Packalen P., Malinen J., Pitkänen J., Maltamo M. (2014). Airborne laser scanning based decision support for wood procurement planning. Special issue: decision support systems for sustainable forest management. Scandinavian Journal of Forest Research 29 (Supplement 1): 132–143. http://dx.doi.org/10.1080/02827581.2013.813063.
Total of 24 references

