Income and time dependence of forest product demand elasticities and implications for forecasting
Buongiorno J. (2015). Income and time dependence of forest product demand elasticities and implications for forecasting. Silva Fennica vol. 49 no. 5 article id 1395. https://doi.org/10.14214/sf.1395
Highlights
- Elasticities of demand with gross domestic product and prices were stable over time and income level for sawnwood and particleboard only
- Other product elasticities differed with income and time, leading in conjunction with a sector model to higher projected world demand and prices than obtained by ignoring differences between countries and over time.
Abstract
In view of improving multi-country forest sector models, this study investigated to what extent the price and income elasticity of demand for forest products had changed in the past two decades, and how much they depended on the countries income level. For each of seven major product groups annual observations were divided between high-income (top 20% in gross domestic product per capita) and low-income, and between recent (2004–2013) and older (1992–2003) observations. The results indicated that for sawnwood and particleboard the data could be pooled across all countries and years. For the other commodity groups (veneer & plywood, fiberboard, newsprint, printing & writing paper, other paper & paperboard), there were statistically significant differences in gross domestic product or price elasticity between high and low-income levels or old and recent observations. Efficient elasticities were obtained by pooling the maximum number of observations while respecting the statistically significant differences. The resulting GDP elasticities were the same, or very close, across income levels for all products. The price elasticities differed by income level only for newsprint and for veneer and plywood. International forest sector projections to 2065 obtained with these elasticities compared with those based on pooling all data across time and income levels gave less than 3% difference for world consumption of sawnwood, particleboard, fiberboard, and newsprint, but 19% higher consumption for veneer and plywood, 31% for printing and writing paper, and 18% for other paper and paperboard. The world price was 1% to 11% higher for end products and 3% to 22% higher for raw materials and intermediate products.
Keywords
modeling;
structural change;
econometrics;
markets
Received 20 May 2015 Accepted 2 September 2015 Published 5 October 2015
Views 88480
Available at https://doi.org/10.14214/sf.1395 | Download PDF

1 Introduction
The objective of this study was to improve the elasticities of demand for forest products used in international models of the forest sector. Although the main target was the Global Forest Products model (GFPM) (Buongiorno and Zhu 2014), the approach and results may be of interest for other models such as the European Forest Institute Global Trade Model (EFI-GTM) (Kallio et al. 2004), the Forestry and Agriculture Sector Optimization Model (FASOM) (Adams et al. 1996), and the Global Biosphere Management Model (GLOBIOM) (Lauri et al. 2013), as well as other studies involving forest products demand.
The most straightforward approach in dealing with multi-country and multi-year data sets is to assume that the demand equation parameters, in particular the income and price elasticities, are the same across countries and constant over time. Consequently, the elasticities are estimated by pooling data from a large number of countries over long time periods (e.g. Simangunsong and Buongiorno 2001; UNECE 2012). This approach has two rationales. First, it has long been argued that science benefits from the pursuit of “Occam’s razor” ideal of simplicity and generality (Baker 2013). This view encourages the development of “parsimonious models” (e.g. Box and Jenkins 1970, p. 17), with the smallest possible number of assumptions and parameters. Second, the goal of statistical efficiency, i.e. parameters of highest precision (minimum standard error) also favors models with few parameters estimated with a large number of observations.
However, even cursory consideration acknowledges that countries differ. In particular there are large income disparities between countries, despite some apparent convergence (Sala-i-Martin 2006). And, wood products are used differently, for example in how lumber is incorporated in residential construction. Furthermore, the way wood products are utilized is constantly changing over time. It is then possible that demand parameters such as gross domestic product (GDP) and price elasticities, widely used in forest sector studies, may vary according to the country condition or the period of observation. Ignoring such effects if they exist leads to biased estimates of the parameters due to significant omitted variables (Wooldridge 2002, p. 63), and consequently erroneous forecasts and policy analyses.
Several past studies of forest products demand differentiate elasticities by income level or other country characteristics (e.g. Buongiorno 1978; Kangas and Baudin 2003; Michinaka et al. 2011). Consideration has also been given to the possibility of changes in the demand elasticities over time (Hetemäki and Obersteiner 2001; Bolkesjø et al. 2003). The study reported here pursued both issues within a unique general framework by considering simultaneously the effect of income level and time period. Specifically, the null hypotheses were that (i) GDP and price elasticities were the same across income level and over time, (ii) at a particular income level, elasticities stayed constant over time, and (iii) during a particular time period, elasticities were the same regardless of income. Then, a sensitivity analysis was carried out with the GFPM forest sector model to determine the economic importance of the differences that were statistically significant.
The paper is organized as follows. It first describes the data base used in the analysis, the econometric model, and the related tests to detect differences between income level or period. The results of these tests are presented next, followed by estimates of efficient demand elasticities that use the maximum number of observations while respecting the statistically significant differences between periods or income groups. Then, these elastiticities are used in the GFPM for long-term projections to assess the differences in consumption and prices resulting from the use of elasticities differentiated by income level and period, compared to elasticities obtained by pooling data from all years and countries. The conclusion summarizes the implications of the findings.
2 Materials and methods
2.1 Demand elasticity estimation
The analysis of the elasticities of demand was done for the following commodity groups, defined as in FAO (2014, p. 24–26):
- sawnwood (coniferous and non coniferous),
- veneer & plywood,
- particleboard,
- fiberboard,
- newsprint,
- printing & writing paper,
- other paper and paperboard.
As the demand elasticities were to be used in the Global Forest Products Model the data were obtained for each of its 180 countries (Buongiorno and Zhu 2014). For each product and country apparent annual consumption was computed as production plus imports minus exports. The annual data series on production, imports, and exports came from the Forestry FAOSTAT data base (FAO 2015). In accord with important changes in country boundaries prior to 1992 the data were collected for 1992 to 2013, the latest year available in FAO (2015). Product prices were estimated as the unit value of imports (import value divided by import quantity) for net importers, and the unit value of exports for net exporters. Real prices in constant United States dollars of 2013 were obtained by deflating nominal prices by the United States GDP deflator (World Bank 2015). The annual data on the gross domestic product of each country, in constant US dollars, from 1992 to 2013 were obtained from the same World Bank Development Indicators data base.
The econometric model used to test the difference in price of income elasticity between countries and time periods was:
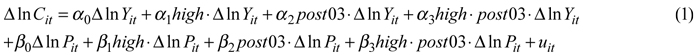
where Δ ln Cit was the yearly change of the natural logarithm of the consumption of a particular product in country i and year t, Δ ln Yit was the yearly change of the natural logarithm of the GDP, and Δ ln Pit was the yearly change of the natural logarithm of the price of the product. The dummy variable high was equal to 1 for countries and years with a GDP per capita above US $15 000 at 2012 prices (20% of all observations), zero otherwise. Post03 was a dummy variable taking the value 1 for years from 2004 to 2013, and 0for 1992 to 2003. The summary statistics for all the variables are in Table 1.
| Table 1. Summary statistics of variables used in estimating demand elasticities1. | |||||||
| Product | Variable | Mean | Mean | SD | Min | Max | Observations |
| Sawnwood | ∆ln Cit | overall | 0.03 | 0.51 | –3.66 | 6.87 | N = 3533 |
| between | 0.12 | –0.94 | 0.46 | n = 179 | |||
| within | 0.50 | –3.64 | 6.43 | T = 19.74 | |||
| ∆ln Pit | overall | –0.001 | 0.36 | –3.20 | 2.18 | N = 3174 | |
| between | 0.07 | –0.44 | 0.32 | n = 175 | |||
| within | 0.36 | –3.16 | 2.14 | T = 18.14 | |||
| Plywood | ∆ln Cit | overall | 0.04 | 0.52 | –3.78 | 3.58 | N = 3192 |
| between | 0.10 | –0.17 | 0.58 | n = 178 | |||
| within | 0.51 | –3.78 | 3.59 | T = 17.93 | |||
| ∆ln Pit | overall | 0.003 | 0.38 | –2.79 | 2.48 | N = 2913 | |
| between | 0.12 | –1.11 | 0.33 | n = 175 | |||
| within | 0.38 | –2.92 | 2.45 | T = 16.65 | |||
| Particleboard | ∆ln Cit | overall | 0.03 | 0.51 | –4.11 | 4.09 | N = 2430 |
| between | 0.13 | –0.69 | 0.80 | n = 152 | |||
| within | 0.50 | –4.10 | 4.11 | T = 15.99 | |||
| ∆ln Pit | overall | 0.002 | 0.37 | –3.54 | 2.52 | N = 2036 | |
| between | 0.10 | –0.67 | 0.24 | n = 139 | |||
| within | 0.36 | –3.41 | 2.55 | T = 14.65 | |||
| Fiberboard | ∆ln Cit | overall | 0.08 | 0.61 | –5.17 | 4.74 | N = 2596 |
| between | 0.12 | –0.24 | 0.55 | n = 159 | |||
| within | 0.60 | –5.17 | 4.77 | T = 16.33 | |||
| ∆ln Pit | overall | 0.005 | 0.37 | –2.41 | 3.21 | N = 2193 | |
| between | 0.07 | –0.22 | 0.34 | n = 151 | |||
| within | 0.36 | –2.43 | 2.96 | T = 14.52 | |||
| Newsprint | ∆ln Cit | overall | 0.03 | 0.40 | –3.07 | 2.64 | N = 2638 |
| between | 0.10 | –0.16 | 0.69 | n = 153 | |||
| within | 0.39 | –3.04 | 2.66 | T = 17.24 | |||
| ∆ln Pit | overall | –0.010 | 0.25 | –1.40 | 1.59 | N = 2539 | |
| between | 0.06 | –0.25 | 0.33 | n = 149 | |||
| within | 0.25 | –1.41 | 1.61 | T = 17.04 | |||
| Printing & writing paper | ∆ln Cit | overall | 0.05 | 0.47 | –2.84 | 4.08 | N = 2947 |
| between | 0.09 | –0.35 | 0.52 | n = 168 | |||
| within | 0.47 | –2.76 | 3.61 | T = 17.54 | |||
| ∆ln Pit | overall | –0.011 | 0.25 | –1.96 | 1.93 | N = 2920 | |
| between | 0.06 | –0.47 | 0.33 | n = 168 | |||
| within | 0.25 | –1.99 | 1.89 | T = 17.38 | |||
| Other paper & paperboard | ∆ln Cit | overall | 0.04 | 0.40 | –4.63 | 4.63 | N = 3119 |
| between | 0.08 | –0.24 | 0.41 | n = 171 | |||
| within | 0.39 | –4.64 | 4.61 | T = 18.24 | |||
| ∆ln Pit | overall | –0.004 | 0.31 | –2.50 | 2.47 | N = 3039 | |
| between | 0.06 | –0.18 | 0.55 | n = 171 | |||
| within | 0.31 | –2.51 | 2.47 | T = 17.77 | |||
| ∆lnYit | overall | 0.05 | 0.14 | –1.06 | 1.38 | N = 3513 | |
| between | 0.03 | –0.03 | 0.21 | n = 172 | |||
| within | 0.13 | –1.02 | 1.38 | T = 20.42 | |||
| rich | overall | 0.20 | 0.40 | 0.00 | 1.00 | N = 3847 | |
| between | 0.37 | 0.00 | 1.00 | n = 175 | |||
| within | 0.15 | –0.62 | 1.16 | T = 21.98 | |||
| post03 | overall | 0.45 | 0.50 | 0.00 | 1.00 | N = 3960 | |
| between | 0.00 | 0.45 | 0.45 | n = 180 | |||
| within | 0.50 | 0.00 | 1.00 | T = 22 | |||
| 1Cit, Pit, Yit = consumption in country i, year t, N = number of observations, n = number of countries, T = average number of observations per country. | |||||||
The α’s and β’s were parameters, and as the variables were all in logarithms, the parameters were elasticities and changes in elasticities over time or between income levels.
The use of yearly changes in this panel data configuration (first differencing over time of multi-country and multi-year data) in equation (1) was meant to eliminate unobserved differences between countries which might affect consumption apart from GDP and price, and the equation was then estimated by robust least squares to correct standards errors from the effects of eventual serial correlation (Wooldridge 2002, p. 279–283). Furthermore, differencing the series was essential to avoid spurious correlation in trended data. The series of consumption and GDP in particular had strong positive trends, averaging 5% per year for GDP and 3% to 8% per year for consumption, depending on the product (Table 1). Consequently, regressions with such trended non-stationary data would lead to spurious results (Verbeek 2008, p. 327).
Then, the following distinct GDP elasticities were obtained by income level and time period:
α0 : GDP elasticity at low income level in 1992 to 2003,
α0+ α1: GDP elasticity at high income level in 1992 to 2003,
α0+ α2: GDP elasticity at low income level in 2004 to 2013,
α0+ α1+ α2+ α3: GDP elasticity at high income level in 2004 to 2013.
In addition to testing the statistical significance of these elasticities against the hypothesis that they were 0, the following hypotheses were tested:
α1 = 0: No income effect on GDP elasticity in 1992 to 2003,
α2 = 0: No period effect on GDP elasticity at low income level,
α1+ α3 = 0: No income effect on GDP elasticity in 2004 to 2013,
α2+ α3 = 0: No period effect on GDP elasticity at high income level.
Parallel elasticity estimates and significance tests were carried out for the price variable using the parameters β0, β1, β2, and β3. An overall homogeneity test was also done with the following hypothesis:
α1 = α2 = α3 = β1 = β2 = β3 = 0: no income or period effect on GDP or price elasticity,
To gain efficiency by maximizing the degrees of freedom and thus minimizing the standard errors, the observations were pooled across income levels or periods whenever a lack of significant statistical difference suggested that it was legitimate to do so. In the case of significant differences between periods, the elasticities in the more recent period were retained for forecasting.
2.2 Forecasting
Statistically different results are not necessarily importand economically (McCloskey 1996). To assess the economic importance of the eventual elasticity differences by country income level or period of observation, it is useful to do sensitivity analysis of the results for different assumptions (Leamer 1985). To this end projections were carried out for the global forest sector up to the year 2065 with the “differentiated elasticities” by period and income, and alternatively with the “pooled elasticities” obtained with observations from all years and countries.
The projections were done with the Global Forest Products Model. All the other parameters of the model except the demand elasticities were held constant. The GFPM calculates for every projected year a global competitive price equilibrium of the production, consumption, imports and exports, across countries and products, linked dynamically to past equilibria.
The GFPM products include the end products studied here, plus fuelwood, industrial roundwood, mechanical pulp, chemical pulp, other fiber pulp, and waste paper. The supply of the raw materials and the demand of the end products are represented by econometric equations. The transformation of products from say, pulp fiber to newsprint, is represented by input-output parameters and attendant manufacturing costs. The model formulation and its computer implementation are described in Buongiorno and Zhu (2014). The current model version deals with 180 countries, forest area and stock and 14 groups of wood products.
In the GFPM simulations the demand for end products shifts over time as a function of the GDP periodic growth rate. In the “pooled elasticities” simulations the GDP and price elasticities were constant across income levels and over time, while with the “differentiated elasticities” they varied with the GDP per capita of individual countries. Other dynamic elements of the GFPM include the change in forest area and forest growth rates and the changes in the input-output coefficients and manufacturing cost, which were the same in both simulations.The input-output (I-O) coefficients and manufacturing costs of the GFPM used in this study were updated with the most recent FAOSTAT data. A recent version of the complete software, its documentation, and a pre-calibrated data set are available freely for academic research (Buongiorno and Zhu 2014).
The global scenario used in the projections from 2012 to 2065 was based on the IPPC scenario of A1B (Nakicenovic et al. 2000), extended and modified for the purpose of the United States Forest Service 2010 RPA Assessment (USDA Forest Service 2012). For the GFPM simulations, the two exogenous variables taken from this scenario were the growth of GDP and population. As GDP growth from the IPCC is available only by region, national GDP growth was deducted from the regional growth in such a way that the regional growth remained the same as in the IPCC and the growth of individual countries converged towards this average regional growth rate. The scenario A1B leads to high income growth and low population growth, and thus high income per capita by the year 2065 which accentuated the projection differences obtained with income-dependent elasticities.
3 Results
3.1 Demand elasticities
3.1.1 Sawnwood
Table 2 shows the econometric results for sawnwood. The elasticities had the expected positive sign for GDP and negative sign for price in both periods at high or low income. At high income, GDP and price elasticities were statistically significant at least at the 5% level in both periods. There was no statistical difference between income levels in either period, and no statistical difference between periods at high or low income. In addition, the homogeneity F test of same elasticities over periods and income levels was not significant at the 5% level. Consequently, efficient estimates were obtained by pooling all observations across income levels and periods. The results, in Table 3, gave a GDP elasticity of 0.24 ± 0.10, significant at the 5% level, and a price elasticity of –0.17 ± 0.05, significant at the 1% level. The GDP elasticity was lower than the median elasticity of nine past studies reported in Simangunsong and Buongiorno (2001), 0.78 for coniferous sawnwood and 0.79 for non coniferous, it was also lower than the values in Michinaka et al. (2011), 0.97 to 1.26 depending on country cluster. The price elasticity was also less in absolute value than the median of nine past studies (–0.35) in Simangunsong and Buongiorno (2001), and the –0.78 to –0.79 in Michinaka et al. (2011).
| Table 2. Sawnwood GDP and price elasticity of demand, by period and country income. | ||||||||
| 1992–2003 | 2004–2013 | Difference | ||||||
| Elast. | SE | Elast. | SE | Elast. | SE | |||
| Low income | ||||||||
| GDP | 0.01 | 0.18 | 0.42 | 0.12 | ** | 0.41 | 0.22 | |
| Price | –0.15 | 0.08 | * | –0.17 | 0.09 | –0.02 | 0.12 | |
| High income | ||||||||
| GDP | 0.38 | 0.14 | ** | 0.55 | 0.14 | ** | 0.18 | 0.20 |
| Price | –0.22 | 0.09 | ** | –0.36 | 0.17 | * | 0.14 | 0.19 |
| Difference | Homogeneity F (6,2883)=1.07 | |||||||
| GDP | 0.37 | 0.23 | 0.13 | 0.18 | ||||
| Price | –0.07 | 0.12 | –0.19 | 0.19 | ||||
| SE = standard error. *,** = significant at 5%, 1%. | ||||||||
| Table 3. Differentiated GDP and price elasticity of demand obtained by pooling data from different periods or income level countries, in the absence of statistically significant differences. | ||||||||
| Commodity | Incomelevel | Years | Elasticity | |||||
| GDP | SE | Price | SE | |||||
| Sawnwood | Low or high | 1992–2013 | 0.24 | 0.10 | * | –0.17 | 0.05 | ** |
| Veneer & plywood | Low | 2004–2013 | 0.72 | 0.11 | ** | –0.33 | 0.05 | ** |
| High | 2004–2013 | 0.72 | 0.11 | ** | –0.61 | 0.12 | ** | |
| Particleboard | Low or high | 1992–2013 | 0.59 | 0.09 | ** | –0.51 | 0.05 | ** |
| Fiberboard | Low or high | 2004–2013 | 0.92 | 0.12 | ** | –0.54 | 0.06 | ** |
| Newsprint | Low | 1992–2013 | 0.42 | 0.06 | ** | –0.25 | 0.05 | ** |
| High | 1992–2013 | 0.39 | 0.17 | * | –0.04 | 0.13 | ||
| Printing & writing | Low or high | 2004–2013 | 0.59 | 0.08 | ** | –0.53 | 0.10 | ** |
| Other paper & paperboard | Low or high | 2004–2013 | 0.40 | 0.08 | ** | –0.45 | 0.06 | ** |
| SE = standard error.*,** = significant at 5%, 1%. | ||||||||
3.1.2 Veneer & plywood
The price and GDP elasticities (Table 4) had the expected sign in both periods and at high or low income, but the GDP elasticity at high income level was not statistically significant in 1992 to 2003. The homogeneity F test rejected the hypothesis of same elasticities across income and periods at the 5% significance level. More precisely, at high income level the GDP elasticity was significantly higher in 2004 to 2013. Furthermore, from 2004 to 2013 the price elasticity was significantly lower at high income level.
| Table 4. Veneer & plywood GDP and price elasticity of demand, by period and country income. | |||||||||
| 1992–2003 | 2004–2013 | Difference | |||||||
| Elast. | SE | Elast. | SE | Elast. | SE | ||||
| Low income | |||||||||
| GDP | 0.59 | 0.13 | ** | 0.66 | 0.12 | ** | 0.08 | 0.18 | |
| Price | –0.37 | 0.07 | ** | –0.33 | 0.05 | ** | 0.04 | 0.09 | |
| High income | |||||||||
| GDP | 0.08 | 0.20 | 0.97 | 0.23 | ** | 0.89 | 0.30 | ** | |
| Price | –0.35 | 0.12 | ** | –0.62 | 0.12 | ** | –0.27 | 0.17 | |
| Difference | Homogeneity F (6,2672)=2.75* | ||||||||
| GDP | –0.51 | 0.24 | ** | 0.30 | 0.26 | ||||
| Price | 0.02 | 0.14 | –0.29 | 0.13 | * | ||||
| SE = standard error. *,** = significant at 5%, 1%. | |||||||||
Taking these differences into account, efficient estimates (Table 3) were obtained by pooling the observations from low and high income levels from 2004 to 2013, while allowing for different price elasticity between income levels. This led to a GDP elasticity of 0.72 ± 0.11 regardless of income, and a price elasticity of –0.33 ± 0.05 at low income and of –0.61 ± 0.12 at high income, all statistically significant at 1% level. The GDP elasticity was less than the median of past studies (1.02) reported in Simangunsong and Buongiorno (2001), but within the cluster-dependent range (0.07 to 1.00) in Michinaka et al. (2011). The price elasticity obtained here was higher in absolute value compared to the median of past studies (–0.18) in Simangunsong and Buongiorno (2001), but within the range (–0.04 to –0.73) in Michinaka et al. (2011).
3.1.3 Particleboard
For particleboard (Table 5), both GDP and price elasticities had the expected signs and they were highly significant at high or low income, and in both periods. The hypothesis of overall homogeneity across income levels and periods could not be rejected at the 5% level (Table 5). In addition, there was no statistically significant difference between income levels within each period, or between periods at a each income level. Therefore, efficient estimates were obtained by pooling data from all income levels and years from 1992 to 2013. The results (Table 3) gave a GDP elasticity of 0.59 ± 0.09 and a price elasticity of –0.51 ± 0.05, both statistically significant at the 1% level. This GDP elasticity was smaller than the median elasticity (1.02) of past studies reported in Simangunsong and Buongiorno (2001), but within the range (0.11 to 1.31) in Michinaka et al. (2011). The price elasticity obtained here was higher in absolute value compared with the median of –0.14 in Simangunsong and Buongiorno (2001), but lower than the range (–0.94 to –1.21) in Michinaka et al. (2011).
| Table 5. Particleboard GDP and price elasticity of demand, by period and country income. | ||||||||
| 1992–2003 | 2004–2013 | Difference | ||||||
| Elast. | SE | Elast. | SE | Elast. | SE | |||
| Low income | ||||||||
| GDP | 0.49 | 0.14 | ** | 0.67 | 0.15 | ** | 0.18 | 0.21 |
| Price | –0.40 | 0.10 | ** | –0.62 | 0.07 | ** | –0.22 | 0.12 |
| High income | ||||||||
| GDP | 0.57 | 0.17 | ** | 0.55 | 0.21 | ** | –0.01 | 0.27 |
| Price | –0.41 | 0.13 | ** | –0.55 | 0.13 | ** | –0.13 | 0.18 |
| Difference | Homogeneity F (6,1871)=0.74 | |||||||
| GDP | 0.08 | 0.22 | –0.12 | 0.26 | ||||
| Price | –0.01 | 0.16 | 0.07 | 0.15 | ||||
| SE = standard error. *,** = significant at 5%, 1%. | ||||||||
3.1.4 Fiberboard
For fiberboard (Table 6), the sign of the price and income elasticity was as expected at both income levels and in both periods, and the elasticity was significant at 5% level except for the price elasticity in 2004–2013. Although the overall F test did not reject the hypothesis of homogeneous elasticities, the more detailed results suggested that the price elasticity was significantly lower at high income from 1992 to 2003. And, at high income, the price elasticity was significantly higher from 2004 to 2013 than earlier. However, there was no significant difference between high and low income in 2004–2013. Consequently, efficient estimates were obtained by pooling the data from 2004 to 2013. The results (Table 3) gave a GDP elasticity of 0.92 ± 0.12 and a price elasticity of –0.54 ± 0.06, both statistically significant at the 1% level. The GDP elasticity was smaller than the median value of 1.38 in past studies (Simangunsong and Buongiorno, 2001), and also smaller than 1.00 in Michinaka et al. (2011). The price elasticity was larger in absolute value than the median of –0.26 in Simangunsong and Buongiorno (2001), and on the high end of the range (–0.03 to –0.50) suggested in Michinaka et al. (2011).
| Table 6. Fiberboard GDP and price elasticity of demand, by period and income level. | |||||||||
| 1992–2003 | 2004–2013 | Difference | |||||||
| Elast. | SE | Elast. | SE | Elast. | SE | ||||
| Low income | |||||||||
| GDP | 1.00 | 0.45 | * | 0.94 | 0.14 | ** | –0.06 | 0.47 | |
| Price | –0.52 | 0.09 | ** | –0.60 | 0.07 | ** | –0.08 | 0.11 | |
| High income | |||||||||
| GDP | 0.81 | 0.24 | ** | 0.79 | 0.23 | ** | –0.02 | 0.33 | |
| Price | –0.85 | 0.10 | ** | –0.32 | 0.165 | 0.53 | 0.19 | ** | |
| Difference | Homogeneity F (6,2070)=0.14 | ||||||||
| GDP | –0.19 | 0.51 | –0.15 | 0.27 | |||||
| Price | –0.32 | 0.14 | * | 0.29 | 0.18 | ||||
| SE = standard error. *,** = significant at 5%, 1%. | |||||||||
3.1.5 Newsprint
The homogeneity F test indicated that there was a significant difference (1% level) in the GDP or price elasticity between income level or time period (Table 7). At low-income the GDP and price elasticity of demand had the expected sign in both periods and they were statistically significant at the 1% level. At high income, the elasticities had the correct sign with data from 1992 to 2003, but with the more recent data the price elasticity was positive, though not significantly different from zero. Within the period 1992–2003, the GDP elasticity was significantly lower at high income. Within 2004–2013 the price elasticity was significantly higher at high income. However, there was no significant difference in GDP or price elasticity between periods, at either low or high income.
| Table 7. Newsprint GDP and price elasticity of demand, by period and income level. | ||||||||
| 1992–2003 | 2004–2013 | Difference | ||||||
| Elast. | SE | Elast. | SE | Elast. | SE | |||
| Low income | ||||||||
| GDP | 0.54 | 0.09 | ** | 0.34 | 0.07 | ** | –0.20 | 0.12 |
| Price | –0.20 | 0.05 | ** | –0.34 | 0.08 | ** | –0.15 | 0.10 |
| Rich | ||||||||
| GDP | 0.08 | 0.17 | 0.57 | 0.25 | * | 0.49 | 0.30 | |
| Price | –0.22 | 0.15 | 0.29 | 0.25 | 0.51 | 0.29 | ||
| Difference | Homogeneity F (6,2381)=3.12** | |||||||
| GDP | –0.46 | 0.19 | * | 0.23 | 0.26 | |||
| Price | –0.02 | 0.16 | 0.64 | 0.26 | * | |||
| SE = standard error. *,** = significant at 5%, 1%. | ||||||||
Thus, highest efficiency (minimum standard error) was obtained by pooling the data at low income, and separately those at high income, from 1992 to 2013. The results (Table 3) gave at low income a GDP elasticity of 0.42 ± 0.06 and price elasticity of –0.25 ± 0.05, both significant at 1% level. At high income levels GDP elasticity was 0.39 ± 0.17, significant at the 5% level, and the price elasticity was –0.04 ± 0.13, not statistically significant. Simangunsong and Buongiorno (2001) report a higher median GDP elasticity of 1.01 for past studies, while Michinaka et al. (2011) find 0.85 to 1.00 depending of country cluster. The price elasticity found here was less in absolute value than the median of –0.54 in Simangunsong and Buongiorno (2001) , but comparable to the finding of Michinaka et al. (2011) of –0.14 to –0.24.
3.1.6 Printing and writing paper
The GDP and price elasticities had the expected sign at high and low income levels and in both time periods, and all were statistically significant at least at the 5% level (Table 8). According to the F test, the hypothesis of homogeneity of elasticities across income level and periods was rejected at the 5% level. The more detailed results indicate that the main difference was between periods at low income: the GDP elasticity was significantly higher in 2004–2013 than earlier. However, within each period, there was no statistically significant difference between low and high income levels. Consequently, efficient estimates were obtained by pooling the data at low and high income levels from 2004 to 2013. This resulted in a GDP elasticity of 0.59 ± 0.08 and a price elasticity of –0.53 ± 0.10, both statistically significant at the 1% level (Table 3). The GDP eslasticity was less than the past studies median (1.30) in Simangunsong and Buongiorno (2001), but larger than the estimate (0.09) in Michinaka et al. (2011). Given the standard errors, the price elasticity was comparable to the past studies median (–0.38) in Simangunsong and Buongiorno (2001), but smaller than the estimate (–0.91) in Michinaka et al. (2011).
| Table 8. Printing & writing paper GDP and price elasticity of demand, by period and income level. | |||||||||
| 1992–2003 | 2004–2013 | Difference | |||||||
| Elast. | SE | Elast. | SE | Elast. | SE | ||||
| Low income | |||||||||
| GDP | 0.23 | 0.10 | * | 0.58 | 0.09 | ** | 0.35 | 0.14 | ** |
| Price | –0.76 | 0.07 | ** | –0.53 | 0.12 | ** | 0.23 | 0.14 | |
| High income | |||||||||
| GDP | 0.45 | 0.19 | * | 0.66 | 0.21 | ** | 0.20 | 0.29 | |
| Price | –0.53 | 0.12 | ** | –0.54 | 0.16 | ** | –0.01 | 0.19 | |
| Difference | Homogeneity F (6,2755)=2.24* | ||||||||
| GDP | 0.23 | 0.22 | 0.08 | 0.23 | |||||
| Price | 0.23 | 0.14 | 0.00 | 0.20 | |||||
| SE = standard error. *,** = significant at 5%, 1%. | |||||||||
3.1.7 Other paper & paperboard
For this product group, both GDP and price elasticities had the expected sign for low and high icome levels and both periods (Table 9). While the GDP elasticity in both income groups was not significantly different from 0in 1992 to 2003 it was highly significant (1% level) in 2004 to 2013. The price elasticity was highly significant in both periods, at both high and low income. Although the hypothesis of homogeneous elasticity across income level and time periods could not be rejected at the 5% level (F statistic, Table 9), the more detailed results showed that the GDP elasticity at low income was significantly (5% level) higher in 2004–2013 than earlier. However, within both periods, there was no significant difference between high and low income levels. Thus the data at both income levels were pooled from 2004 to 2013 to obtain efficient estimates of GDP elasticity of 0.40 ± 0.08 and of price elasticity of –0.45 ± 0.06, both significant at 1% level (Table 3). The GDP elasticity was smaller than the past studies median (1.13) in Simangunsong and Buongiorno (2001), and also smaller than the cluster dependent range (0.65 to 1.10) in Michinaka et al. (2011). The price elasticity was larger in absolute value that the median (–0.30) in Simangunsong and Buongiorno (2001), but larger than the estimate (–0.15) in Michinaka et al. (2011).
| Table 9. Other paper & paperboard GDP and price elasticitity of demand, by period and income level. | |||||||||
| 1992–2003 | 2004–2013 | Difference | |||||||
| Elast. | SE | Elast. | SE | Elast. | SE | ||||
| Low income | |||||||||
| GDP | 0.16 | 0.08 | 0.40 | 0.09 | ** | 0.25 | 0.12 | * | |
| Price | –0.33 | 0.08 | ** | –0.43 | 0.072 | ** | –0.10 | 0.11 | |
| High income | |||||||||
| GDP | 0.36 | 0.19 | 0.37 | 0.12 | ** | 0.01 | 0.23 | ||
| Price | –0.29 | 0.09 | ** | –0.52 | 0.09 | ** | –0.24 | 0.13 | |
| Difference | Homogeneity F (6,2839)=1.6 | ||||||||
| GDP | 0.20 | 0.21 | –0.03 | 0.152 | |||||
| Price | 0.04 | 0.12 | –0.10 | 0.11 | |||||
| SE = standard error. *,** = significant at 5%, 1%. | |||||||||
3.2 Consequences for forecasting
The projected consumption in 2065 obtained with the GFPM model and either the demand elasticities differentiated by income level and time period (Table 3), or the elasticities obtained by pooling all the data (Table 10) showed less than 1% difference for sawnwood, particleboard, and fiberboard, globally and by major geographic region. Accordingly the details are not shown here. As the demand elasticities were the same for sawnwood and particleboard and similar for fiberboard in the two simulations, the only potential differences came from differences in the price of industrial roundwood induced by different demand for the other products. Although the world price of industrial roundwood was 6% higher in 2065 with the differentiated elasticities (Table 11), this was not enough to significantly affect the demand for sawnwood, particleboard and fiberboard.
| Table 10. GDP and price elasticity obtained by pooling all countries and years from 1992 to 2013. | ||||||
| Elasticity | ||||||
| Commodity | GDP | SE | Price | SE | ||
| Sawnwood | 0.24 | 0.10 | ** | –0.17 | 0.05 | ** |
| Veneer & plywood | 0.62 | 0.08 | ** | –0.37 | 0.04 | ** |
| Particleboard | 0.59 | 0.09 | ** | –0.51 | 0.05 | ** |
| Fiberboard | 0.93 | 0.15 | ** | –0.58 | 0.05 | ** |
| Newsprint | 0.43 | 0.06 | ** | –0.22 | 0.04 | ** |
| Printing & writing | 0.44 | 0.06 | ** | –0.65 | 0.05 | ** |
| Other paper | 0.29 | 0.06 | ** | –0.38 | 0.05 | ** |
| SE = standard error. ** = significant at 1%. | ||||||
| Table 11. World export prices in 2065 with demand elasticities differentiated by period and income level (a), or based on all pooled data (b). | |||||
| Product | Unit | 2012 | 2065 (a) | 2065 (b) | Difference (a)/(b)–1 |
| Industrial roundwood | $/m3 | 108 | 162 | 153 | 0.06 |
| Sawnwood | $/m3 | 269 | 354 | 343 | 0.03 |
| Veneer & plywood | $/m3 | 596 | 1048 | 991 | 0.06 |
| Particleboard | $/m3 | 280 | 556 | 549 | 0.01 |
| Fiberboard | $/m3 | 443 | 908 | 897 | 0.01 |
| Mechanical pulp | $/t | 474 | 978 | 945 | 0.03 |
| Chemical pulp | $/t | 602 | 994 | 964 | 0.03 |
| Other fiber pulp | $/t | 1234 | 1719 | 1619 | 0.06 |
| Waste paper | $/t | 174 | 568 | 464 | 0.22 |
| Newsprint | $/t | 639 | 763 | 687 | 0.11 |
| Printing & writing | $/t | 960 | 1092 | 1011 | 0.08 |
| Other paper & paperboard | $/t | 1004 | 1574 | 1499 | 0.05 |
Larger differences occurred for veneer and plywood, newsprint, printing and writing paper, and paper and paperboard. For newsprint (Table 12) the projected world demand was lower in 2065 with differentiated elasticities, but only by 3%. For the other three products, the projected consumption in 2065 was higher with the differentiated elasticities than with the elasticities based on all pooled data. For veneer and plywood (Table 12) world consumption was 19% higher globally, with largest differences in Asia and Africa, and smallest (2%) in Europe and North America. For printing and writing paper (Table 13), global consumption was 31% higher with the differentiated elasticity. The percent difference was markedly higher in Asia, Africa, and South America than in Europe and North America. Similar regional differences occurred for other paper and paperboard for which global consumption was 18% higher with the differentiated elasticities (Table 13).
| Table 12. Observed and predicted consumption of veneer & plywood, and newsprint in 2065, by region and selected countries, with demand elasticities differentiated by period and income level (a), or based on all pooled data (b). | ||||||||
| Veneer & plywood (106 m3) | Newsprint (106 t) | |||||||
| 2012 | 2065 (a) | 2065 (b) | 2012 | 2065 (a) | 2065 (b) | |||
| AFRICA | 2.7 | 17.6 | 13.1 | 0.4 | 2.6 | 2.7 | ||
| Egypt | 0.6 | 3.9 | 3.1 | 0.1 | 0.4 | 0.4 | ||
| Nigeria | 0.2 | 1.7 | 1.3 | 0.0 | 0.3 | 0.3 | ||
| South Africa | 0.2 | 0.5 | 0.5 | 0.2 | 0.5 | 0.5 | ||
| N/C AMERICA | 17.0 | 28.2 | 28.6 | 13.0 | 8.3 | 8.6 | ||
| Canada | 3.6 | 5.1 | 5.3 | 0.3 | 0.6 | 0.6 | ||
| Mexico | 0.8 | 2.7 | 2.5 | 0.4 | 0.9 | 0.9 | ||
| United States | 12.2 | 19.2 | 19.9 | 12.2 | 6.4 | 6.6 | ||
| SOUTH AMERICA | 3.7 | 11.6 | 10.3 | 0.9 | 2.8 | 2.9 | ||
| Argentina | 0.1 | 0.3 | 0.3 | 0.3 | 0.4 | 0.4 | ||
| Brazil | 1.9 | 5.4 | 4.9 | 0.3 | 1.1 | 1.2 | ||
| Chile | 0.5 | 1.1 | 1.1 | 0.1 | 0.1 | 0.1 | ||
| ASIA | 92.8 | 437.4 | 360.4 | 7.6 | 38.2 | 39.5 | ||
| China | 70.8 | 347.7 | 287.1 | 1.1 | 12.7 | 13.1 | ||
| India | 3.0 | 26.7 | 19.3 | 0.6 | 10.7 | 11.2 | ||
| Indonesia | 3.8 | 21.9 | 17.4 | 0.1 | 1.7 | 1.7 | ||
| Japan | 6.4 | 7.6 | 8.2 | 3.7 | 4.2 | 4.3 | ||
| Korea, Republic of | 2.1 | 4.2 | 4.2 | 0.8 | 1.4 | 1.4 | ||
| Malaysia | 1.0 | 3.5 | 3.1 | 0.2 | 1.1 | 1.1 | ||
| OCEANIA | 1.4 | 2.8 | 2.7 | 0.7 | 1.0 | 1.0 | ||
| Australia | 0.5 | 0.7 | 0.8 | 0.6 | 0.7 | 0.8 | ||
| New Zealand | 0.8 | 1.3 | 1.4 | 0.1 | 0.2 | 0.2 | ||
| EUROPE | 10.7 | 22.3 | 21.7 | 9.1 | 13.8 | 14.2 | ||
| EU-28 | 8.1 | 14.5 | 14.6 | 7.8 | 10.8 | 11.2 | ||
| Austria | 0.1 | 0.1 | 0.1 | 0.4 | 0.3 | 0.3 | ||
| Finland | 0.3 | 0.3 | 0.3 | 0.1 | 0.1 | 0.1 | ||
| France | 0.7 | 0.9 | 1.0 | 0.7 | 0.8 | 0.8 | ||
| Germany | 1.4 | 1.7 | 1.8 | 2.1 | 2.8 | 2.9 | ||
| Italy | 0.9 | 1.1 | 1.1 | 0.6 | 1.0 | 1.0 | ||
| Russian Federation | 2.1 | 6.5 | 6.0 | 0.9 | 1.4 | 1.5 | ||
| Spain | 0.3 | 0.4 | 0.4 | 0.5 | 0.2 | 0.2 | ||
| Sweden | 0.2 | 0.2 | 0.3 | 0.5 | 0.5 | 0.5 | ||
| United Kingdom | 1.3 | 1.8 | 1.9 | 1.9 | 2.3 | 2.4 | ||
| WORLD | 128.3 | 519.8 | 436.9 | 31.7 | 66.7 | 68.9 | ||
| Table 13. Observed and predicted consumption of printing & writing paper, and other paper & paperboard in 2065, by region and selected countries, with demand elasticities differentiated by period and income level (a), or based on all pooled data (b). | |||||||
| Printing & writing paper (106 t) | Other paper & paperboard (106 t) | ||||||
| 2012 | 2065 (a) | 2065 (b) | 2012 | 2065 (a) | 2065 (b) | ||
| AFRICA | 2.0 | 10.8 | 7.2 | 4.1 | 10.0 | 7.8 | |
| Egypt | 0.4 | 2.2 | 1.4 | 1.0 | 2.9 | 2.2 | |
| Nigeria | 0.1 | 1.5 | 0.9 | 0.2 | 0.8 | 0.6 | |
| South Africa | 0.8 | 2.0 | 1.6 | 1.6 | 2.5 | 2.2 | |
| N/C AMERICA | 21.6 | 42.5 | 36.3 | 59.5 | 80.9 | 74.1 | |
| Canada | 1.5 | 2.7 | 2.3 | 3.5 | 4.3 | 4.0 | |
| Mexico | 1.3 | 3.8 | 2.8 | 5.6 | 10.0 | 8.3 | |
| United States | 18.5 | 34.7 | 30.3 | 48.9 | 63.3 | 59.1 | |
| SOUTH AMERICA | 4.1 | 12.9 | 9.8 | 11.2 | 20.1 | 17.3 | |
| Argentina | 0.6 | 1.7 | 1.3 | 1.0 | 1.7 | 1.5 | |
| Brazil | 2.1 | 6.2 | 4.8 | 7.1 | 12.6 | 10.8 | |
| Chile | 0.3 | 0.8 | 0.7 | 1.0 | 1.2 | 1.3 | |
| ASIA | 48.6 | 183.4 | 132.1 | 127.7 | 267.4 | 216.8 | |
| China | 24.1 | 97.9 | 70.2 | 77.1 | 171.7 | 137.7 | |
| India | 4.1 | 26.2 | 16.9 | 5.4 | 15.9 | 12.0 | |
| Indonesia | 2.1 | 9.9 | 6.6 | 4.5 | 11.0 | 8.6 | |
| Japan | 9.6 | 13.3 | 12.4 | 14.5 | 15.6 | 15.3 | |
| Korea, Republic of | 1.4 | 3.5 | 2.9 | 6.7 | 9.9 | 8.9 | |
| Malaysia | 0.6 | 1.9 | 1.4 | 2.4 | 4.2 | 3.6 | |
| OCEANIA | 1.4 | 2.7 | 2.3 | 2.3 | 3.1 | 2.8 | |
| Australia | 1.3 | 2.3 | 2.0 | 1.9 | 2.4 | 2.3 | |
| New Zealand | 0.2 | 0.3 | 0.3 | 0.4 | 0.5 | 0.5 | |
| EUROPE | 27.2 | 49.5 | 42.8 | 57.8 | 76.5 | 70.1 | |
| EU-28 | 24.8 | 43.0 | 37.8 | 49.4 | 61.6 | 57.5 | |
| Austria | 0.4 | 0.5 | 0.5 | 1.7 | 1.8 | 1.8 | |
| Finland | 0.0 | 0.2 | 0.2 | 1.1 | 1.0 | 1.0 | |
| France | 3.3 | 5.3 | 4.8 | 5.5 | 6.4 | 6.1 | |
| Germany | 6.7 | 9.4 | 8.8 | 11.2 | 12.2 | 11.9 | |
| Italy | 2.7 | 4.0 | 3.7 | 6.8 | 7.5 | 7.3 | |
| Russian Federation | 0.8 | 2.6 | 2.0 | 5.3 | 9.6 | 8.1 | |
| Spain | 1.5 | 2.5 | 2.2 | 4.5 | 5.2 | 5.0 | |
| Sweden | 0.5 | 0.4 | 0.4 | 1.5 | 1.1 | 1.1 | |
| United Kingdom | 3.2 | 5.5 | 4.9 | 4.6 | 5.6 | 5.3 | |
| WORLD | 104.9 | 301.7 | 230.6 | 262.7 | 457.9 | 389.0 | |
For all products, the world price, represented by the unit value of world exports, was higher in 2065 with the differentiated than with the pooled elasticities (Table 11). While the price difference was negligible for particleboard and fiberboard, it reached 22% for waste paper as a result of its increased demand induced by the higher consumption of printing and writing paper and other paper and paperboard (Table 13).
4 Summary and discussion
With the general objective of improving forecasts and policy analyses based on multi-country models of the forest sector, this paper investigated the hypothesis that the elasticities of demand for forest products varied concurrently by country income level and by period of observation. To this end, data from 180 countries observed from 1992 to 2013 were divided between high income (the 20% top observations according to GDP per capita) and low income. Within each group the data were further subdivided between recent (post 2003) and earlier observations (1992–2003). A panel data analysis of a demand model in yearly first differences was used to estimate the GDP and price elasticities and their variations in time within each income group and between income groups within each time period. Sensitivity analysis was then carried out with a sector model to assess the economic importance of the observed statistical differences for forecasting.
The econometric results showed complete homogeneity of the elasticities over time and income level for sawnwood and particleboard. For the other products there was a significant statistical difference either between income levels in a period, or between periods in an income group. For forecasting purpose, efficient elasticity estimates were then obtained by pooling observations where and when no statistical difference existed between income levels or periods. In cases of differences between periods, as for veneer and plywood, fiberboard, printing and writing paper, and other paper and paperboard, the most recent period (2004–2013) was used. The resulting GDP elasticities were the same, or very close, across income levels for all products. The price elasticities differed by income level only for newsprint (–0.25 for low income countries and –0.04 for high income), and for veneer and plywood (–0.33 for low income countries and –0.61 for high income).
Since the forest products considered here serve as raw material input in making other products (for example plywood is used to build houses), one explanation for the changes of elasticities is technical change in the techniques of production, such as in house construction. Similarly, for paper and paperboard, a possible explanation for the changes of elasticities is the change in information media and/or packaging. Such changes could be induced by development (explaining the role of income level), or simply by the discovery of new techniques over time (Zhang and Buongiorno 1997, 1998)
These differentiated elasticities were then used for long-term projections with the GFPM and the results compared with projections obtained with elasticities based on pooling all data across years and countries. The differenciated elasticities gave substantially higher projections of world consumption in 2065 for veneer and plywood (19%), printing and writing paper (31%), and other paper and paperboard (18%), but less than 3% difference for sawnwood, partibleboard, fiberboard and newsprint. The world price was 1% to 11% higher for end products and 3% to 22% higher for raw materials and intermediate products.
The results of this study suggest that it is advisable for modelers to constantly update parameters as new data become available, test for structural change, exercise care in pooling data across countries, and do sensitivity analysis to determine the economic importance of statistically significant differences. Still, while the two sets of elasticities gave substantially different projections for some products, it is not certain which one is better for forecasting. Although they might be biased, the pooled elasticities (Table 10) tended to be more precise than the differentiated ones, especially for newsprint for which the differentiated price elasticity was not statistically significant at high income levels (Table 3).
More importantly, while the analysis showed, with a high level of probability, that some (but not all) elasticities had changed in the past, and that they were in some cases different between high and low income levels, if and how the elasticities will change in the future remains an open question. The ability of econometrics to predict these changes is limited, and it seems reasonable that it must be supplemented by judgement (Goodwin et al. 2011; Wright et al. 1996), although one should always “guard against the tendency to overestimate the value of personal insights” (McNees 1990). Formal sensitivity analysis similar to that done above to determine the economic impact of different parameters remains essential to assess the uncertainty of long-term projections.
Acknowledgments
The research leading to this paper was supported in part by a joint venture agreement between the University of Wisconsin and the USDA Forest Service Southern Forest Research Station, in cooperation with project leader Jeff Prestemon.
References
Adams D.M., Alig R.J., McCarl B.A., Callaway J.M. ,Winnett S.M. (1996). The forest agricultural sector optimization model: model structure and applications. U.S. Department of Agriculture, Forest Service, Pacific Northwest Research Station, Portland, OR, Research Paper PNW-495. 44 p.
Baker A. (2013). Simplicity. In: Zalta E.N. (ed.). The Stanford encyclopedia of philosophy (Fall 2013 edition). http://plato.stanford.edu/archives/fall2013/entries/simplicity/. [Cited 15 May 2013].
Bolkesjø T.F., Obersteiner M., Solberg B. (2003). Information technology and the newsprint demand in Western Europe: a Bayesian approach. Canadian Journal of Forest Research 33: 1644–1652. http://dx.doi.org/10.1139/x03-083.
Box G.E.P., Jenkins G.M. (1970). Time series analysis forecasting and control. Holden-Day, San Francisco. 553 p.
Buongiorno J. (1978). Income and price elasticities in the world demand for paper and paperboard. Forest Science 24(2): 231–246.
Buongiorno J, Zhu S. (2014). Using the global forest products model (GFPM version 2014 with BPMPD). Madison (WI), Department of Forest Ecology and Management, University of Wisconsin, Staff paper series 80. http://labs.russell.wisc.edu/buongiorno/welcome/gfpm/. [Cited 1 March 2015].
FAO (2014). FAO Yearbook of Forest Products 2008-2012. Food and Agriculture of the United Nations, Rome. 358 p.
FAO (2015). FAOSTAT Forestry data base. Food and Agriculture Organization of the United Nations, Rome. http://faostat3.fao.org/download/F/FO/E. [Cited 22 March, 2015].
Goodwin P., Önkal D., Lawrence M. (2011). Improving the role of judgment in economic forecasting. p. 163–192. In: Clemens M.P., Hendry D.F. (eds.). The Oxford handboodk of economic forecasting. Oxford University Press. 713 p. http://dx.doi.org/10.1093/oxfordhb/9780195398649.013.0007.
Hetemäki L., Obersteiner M. ( 2001). US newsprint demand forecasts to 2020: classical and Bayesian approaches. International Institute for Applied Systems Analysis, Laxenburg, Austria, Interim Report IR-01-070. 47p.
Kallio A.M.I., Moiseyev A., Solberg B. (2004). The global forest sector model EFI-GTM – the model structure. European Forest Institute, Joensuu, Finland, EFI Technical Report 15. 24 p.
Kangas K., Baudin A. (2003). Modelling and projections of forest products demand, supply and trade in Europe. UN/FAO European forest sector outlook studies. UNECE, Geneva. http://www.unece.org/fileadmin/DAM/timber/docs/efsos/03-sept/dp-30.pdf. [Cited 21 Sept 2015].
Lauri P., Havlik P., Kindermann G., Forsell N., Bottcher H., Obersteiner M. (2013). Woody biomass energy potential in 2050. Energy Policy 66: 19–31. http://dx.doi.org/10.1016/j.enpol.2013.11.033.
Leamer E.E. (1985). Sensitivity analysis would help. American Economic Review 75(3): 308–13.
McCloskey D.N. (1996). The loss function has been mislaid: the rethoric of significance tests. American Economic Review 75(2): 201–210.
McNees S.K. (1990). The role of judgment in forecasting. International Journal of Forecasting 6(3): 287–299. http://dx.doi.org/10.1016/0169-2070(90)90056-H.
Michinaka T., Tachibana S., Turner J. (2011). Estimating price and income elasticities of demand for forest products: cluster analysis used in grouping. Forest Policy and Economics 13(6): 435–445. http://dx.doi.org/10.1016/j.forpol.2011.05.011.
Nakicenovic N., Davidson O., Davis G., Grübler A., Kram T., Lebre La Rovere E., Metz B., Morita T., Pepper W., Pitcher H., Sankovski A., Shukla P., Swart R., Watson R., Zhou D. (2000). Special report on emissions scenarios: a special report of working group III of the intergovernmental panel on climate change. Cambridge University Press, Cambridge, U.K. 599 p. http://www.grida.no/climate/ipcc/emission/index.htm. [Cited 6 May 2015].
Sala-i-Martin X. (2006). The world distribution of income: falling poverty and convergence, period. Quarterly Journal of Economics 121(2): 351–397. http://dx.doi.org/10.1162/qjec.2006.121.2.351.
Simangunsong B.C.H., Buongiorno J. (2001). International demand equations for forest products: a comparison of methods. Scandinavian Journal of Forest Research 16(2): 155–172. http://dx.doi.org/10.1080/028275801300088242.
UNECE (2012). The North American forest sector outlook study. ECE/TIM/29. United Nations Commission for Europe, Geneva. 65 p.
USDA Forest Service (2012). Future of America’s forest and rangelands: forest service 2010 resources planning act assessment. United States Department of Agriculture, Forest Service, Washington DC, General Technical Report WO-87. 197 p.
Verbeek M. (2008). A guide to modern econometrics. 3rd edition. Wiley, San Francisco, CA. 472 p.
Wooldridge J.M. (2002). Econometric analysis of cross section and panel data. The MIT Press, Cambridge. 752 p.
World Bank (2015). World Bank development indicators data base. http://databank.worldbank.org/data/views/variableSelection/selectvariables.aspx?source=world-development-indicators. [Cited 18 May 2015].
Wright G., Lawrence M.J., Collopy F. (1996). The role and validity of judgment in forecasting. International Journal of Forecasting 12(1): 1–8. http://dx.doi.org/10.1016/0169-2070(96)00674-7.
Zhang Y., Buongiorno J. (1997). Communication media and demand for printing and publishing papers in the United States. Forest Science 43(3): 362–377.
Zhang Y., Buongiorno J. (1998). Paper or plastic? – The United States demand for paper and paperboard in packaging. Scandinavian Journal of Forest Research 13(1–4): 54–65. http://dx.doi.org/10.1080/02827589809382962.
Total of 28 references.
Send to email


