Divergent response of tree-ring width and maximum latewood density of Abies faxoniana to warming trends at the timberline of the western Qinling Mountains and northeastern Tibetan Plateau, China
Chen F., Yuan Y., Wei W., Zhang T., Shang H., Yu S. (2015). Divergent response of tree-ring width and maximum latewood density of Abies faxoniana to warming trends at the timberline of the western Qinling Mountains and northeastern Tibetan Plateau, China. Silva Fennica vol. 49 no. 4 article id 1155. https://doi.org/10.14214/sf.1155
Highlights
- We describe new tree-ring width and maximum latewood density chronologies of Faxon fir
- Temperature is the most important limiting factor for the radial growth of Faxon fir
- The tree-ring width series captured the warming trends and allowed detecting the recent warming in a long-term context, while the maximum latewood density series showed no upward trend.
Abstract
Tree-ring width (TRW) and maximum latewood density (MXD) data of Faxon fir (Abies faxoniana Rehd. et Wils.) were analyzed for five timberline sites in the western Qinling Mountains and northeastern Tibetan Plateau, to investigate their relationships to climate change, especially twentieth century warming. The cross-correlations among TRW chronologies at the low-frequency band were higher, while the higher correlations among MXD chronologies were found at the high-frequency band. Response analysis showed that the tree-ring formation of fir trees was significantly and positively affected by temperature variations, while it was also negatively affected by precipitation. The TRW series captured the warming trends and allowed detecting the recent warming in a long-term context, while the MXD series showed no upward trend. We also found the temperature sensitivity of the TRW series is unstable over space and time. The divergent response between TRW and MXD might be caused by the seasonal variations of warming trends.
Keywords
dendroclimatology;
tree rings;
faxon fir;
climate-growth relationships;
warming trend
-
Chen,
Key Laboratory of Tree-ring Physical and Chemical Research of China Meteorological Administration/Xinjiang Laboratory of Ecology, Institute of Desert Meteorology, China Meteorological Administration, 46 Jianguo Road, Urumqi 830002, China
E-mail
feng653@163.com

- Yuan, Key Laboratory of Tree-ring Physical and Chemical Research of China Meteorological Administration/Xinjiang Laboratory of Ecology, Institute of Desert Meteorology, China Meteorological Administration, 46 Jianguo Road, Urumqi 830002, China E-mail yuanyuj5502@sina.com
- Wei, Key Laboratory of Tree-ring Physical and Chemical Research of China Meteorological Administration/Xinjiang Laboratory of Ecology, Institute of Desert Meteorology, China Meteorological Administration, 46 Jianguo Road, Urumqi 830002, China E-mail cycfqq@sohu.com
- Zhang, Key Laboratory of Tree-ring Physical and Chemical Research of China Meteorological Administration/Xinjiang Laboratory of Ecology, Institute of Desert Meteorology, China Meteorological Administration, 46 Jianguo Road, Urumqi 830002, China E-mail tongwenzhang19820705@hotmail.com
- Shang, Key Laboratory of Tree-ring Physical and Chemical Research of China Meteorological Administration/Xinjiang Laboratory of Ecology, Institute of Desert Meteorology, China Meteorological Administration, 46 Jianguo Road, Urumqi 830002, China E-mail shang8632@163.com
- Yu, Key Laboratory of Tree-ring Physical and Chemical Research of China Meteorological Administration/Xinjiang Laboratory of Ecology, Institute of Desert Meteorology, China Meteorological Administration, 46 Jianguo Road, Urumqi 830002, China E-mail yushl@idm.cn
Received 26 March 2014 Accepted 17 February 2015 Published 27 August 2015
Views 161347
Available at https://doi.org/10.14214/sf.1155 | Download PDF

1 Introduction
With an average elevation of more than 4000 m a.s.l., the Tibetan Plateau is one of the most sensitive regions to climatic change (Zheng 1996). The Qinling Mountains is a major east-west mountain range, and is also an important dividing line between warm-temperate and subtropical zones in East Asia. The Qinling Mountains provide a natural boundary between the north and south of China, and have an important role in climate and ecosystem processes. Timberlines of the Tibetan Plateau and Qinling Mountains are characterized by severe climatic conditions (mean annual temperature is 1.7 °C) and short growing seasons for plants. Therefore, trees from this region are believed to be sensitive to climatic changes. As a part of the Shangri-La, the timberlines of this region are covered by widespread forests dominated by various coniferous species that have great potential for dendroclimatological studies (Wang et al. 2013). Dendroclimatological records from the Tibetan Plateau and Qinling Mountains show that, despite a complex mountain terrain and spatial differences in local temperature and tree-ring growth, it is possible to develop temperature models using regional networks of tree-ring sites (i.e. Hughes et al. 1994; Garfin et al. 2005; Gou et al. 2007; Liu et al. 2008; Liang et al. 2009; Fan et al. 2009; Wang et al. 2009). However, compared to other continents, such as Europe and North America, the number of tree-ring investigation sites from the Qinling Mountains and the northeastern Tibetan plateau is low, and no tree-ring density study has been carried out in the western Qinling Mountains and northeastern Tibetan Plateau yet.
It is generally assumed in tree-ring studies that the approximate relationship between tree-ring growth and the limiting climate factor is stable over time (Fritts 1976). However, recent research results have reported problems with this assumption. Either formerly temperature sensitive tree ring chronologies have reduced sensitivity to temperature at high northern latitudes (Briffa et al. 1998; Jacoby et al. 2000; Solberg et al. 2002), increased in sensitivity (Wilmking et al. 2005), or even changed from positive to negative temperature sensitivity (Wilmking and Myers-Smith 2008). In addition, many dendrochronological studies have revealed that radial growth of trees near the timberlines increased under global warming (Ettl and Peterson 1995; Buckley et al. 1997; Peterson and Peterson 2001). Thus, the warming trends and their effects on tree-ring growth have caused wide public concern over the recent years (Briffa et al. 1998; Lloyd and Fastie 2002; Wilmking et al. 2005; Driscoll et al. 2005; D’Arrigo et al. 2004, 2008; Esper et al. 2010). To improve our understanding of tree rings as proxies for large-scale climate reconstructions and to estimate the ecological responses of trees to climate change, more detailed knowledge about the influence of climate change on tree-ring growth is also needed.
In this study, we developed new chronologies of tree-ring width (TRW) and maximum latewood density (MXD) of Faxon fir (Abies faxoniana Rehd. et Wils.) trees grown at the timberline of the western Qinling Mountains and northeastern Tibetan Plateau, China. The goals of this study are: (1) to investigate the important controlling factors on the Faxon fir radial growth; and (2) to assess the response of tree-ring parameters to recent warming.
2 Materials and methods
2.1 Study area
The study areas are located in the western Qinling Mountains and northeastern Tibetan Plateau, China (Fig. 1). The climate of this region is strongly influenced by the Asian monsoon. The climate of timberline area is characterized by cold, windy winters and wet summers. There are four vegetation zones arranged with elevation varying from 700 m a.s.l. to 3400 m a.s.l.. The fir forest extends from 2600 m a.s.l. to 3400 m a.s.l., which is the altitudinal timberline. The timberline is actually a zone of transition between fir forests and the alpine meadows, which is composed of fascicular fir trees and tree islands. They are dominated by Faxon fir (Fig. 2). The soils in the study area are mainly acid umber and podzolic soil. The study areas were chosen for the following reasons: (1) the areas are unlikely to be affected by anthropogenic activity, (2) fir timberlines in this region are typical fir timberline in China and (3) the zone is a transitional zone between the Tibetan Plateau and warm temperature zone.
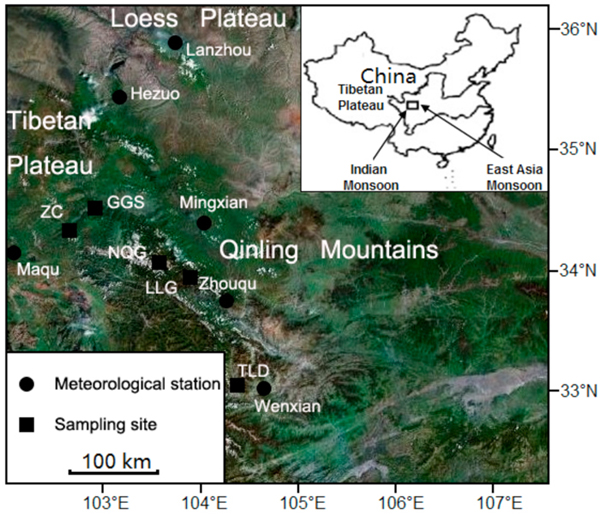
Fig. 1. Locations of tree-ring sites and meteorological stations in the western Qinling Mountains and northeastern Tibetan Plateau, China.

Fig. 2. Faxon fir forest at the timberline sites in the western Qinling Mountains and northeastern Tibetan Plateau, China, and a typical Faxon fir tree sampled in this study.
2.2 Tree-ring sampling and chronology development
During the 2006 and 2009 summer field seasons, Faxon fir trees were sampled at five timberline sites (site code ZC, TLD, LLG, NQG and GGS). This network covers an area from northeastern Tibetan Plateau in the west to the western part of the Qinling Mountains in the east, slopes range from 10 to 50%, but are generally 20–35% and site elevations range from 3100 to 3350 m a.s.l. To minimize non-climatic effects on the radial growth, only trees with no injury and disease were sampled. In total 152 5-mm diameter cores and 130 10-mm diameter cores from 111 trees were collected. Site information is listed in Table 1. All cores from the timberline sites ZC, TLD, LLG, and GGS were processed for TRW and the 10-mm diameter cores from the timberline sites ZC, NQG and GGS were also processed for MXD. Due to the serious damages during the transport process, the cores from NQG site were not used for TRW.
| Table 1. Information about the sampling sites in the western Qinling Mountains and northeastern Tibetan Plateau. | ||||||
| Site | Latitude (N) | Longitude (E) | Trees / 5-mm diameter cores / 10-mm diameter cores number | Elevation (m) | Aspect | Slope |
| LLG | 34°07´ | 103°48´ | 21/38/0 | 3120–3200 | NW | 10–50° |
| NQG | 34°09´ | 103°31´ | 21/21/42 | 3100–3190 | N | 20–40° |
| TLD | 32°56´ | 104°17´ | 24/48/0 | 3200–3280 | E | 20–30° |
| ZC | 34°26´ | 102°43´ | 23/23/44 | 3300–3320 | N | 20–40° |
| GGS | 34°20´ | 102°59´ | 22/22/44 | 3310–3350 | NE | 30–40° |
After mounting and progressively sanding to >400 grit, the cores were subjected to standard graphical dating methods (Stokes and Smiley 1968). After annual ring widths were measured to the nearest 0.001 mm using a Velmex measuring system, we used the program COFECHA (Holmes 1983) to test the accuracy of crossdating of TRW. Cores were cut into 1.0 ± 0.02 mm -thin sections with a twin-blade saw (DENDRO CUT 2003), with the angles vertical to the wood fiber, adjusted by a DENDROSCOPE. The thin sections were then put into a room with constant temperature and humidity for at least 2 h before X-ray photography was taken in the same room (Wang et al. 2009). The grey-scale variations of the X-ray film were then measured by the DENDRO2003 tree-ring workstation with a resolution of 0.01 mm, and brightness variations transferred into g/cm3 using a calibration wedge (Eschbach et al. 1995). Relationships between the absolute (volume and mass) and radiographic (X-ray) wood density were employed as correction factors (Schweingruber et al. 1978; Cleaveland 1986; Büntgen et al. 2010).
To remove non-climatic trends due to age, size, and stand dynamics (Fritts 1976) from the raw measurements, each individual TRW and MXD series was fit with a cubic smoothing spline with a 50% frequency response at 67% of the series length (Cook and Kairiukstis 1990). Standardization was performed using the ARSTAN program. The detrended data from individual tree cores were combined into site chronologies using a bi-weight robust mean (Cook and Kairiukstis 1990). The bi-weight robust mean minimizes the influence of outliers, extreme values or biases in tree-ring indices (Cook and Kairiukstis 1990). The variance in chronologies was stabilized in the chronology compilation process with the Briffa Rbar-weighted method (Osborn et al. 1997), which uses average correlations between series in combination with sample size each year to make adjustments in the variance for changes in sample size. Final chronologies were truncated at <5 series. Inter-series correlation (Rbar) and the expressed population signal (EPS) were calculated for 50-year windows lagged by 25 years along the time-series to assess their signal strength (Wigley et al. 1984). The ARSTAN program produces three versions of standardized chronologies: Standard, Residual and Arstan. We used the standard version of the MXD and TRW chronologies, which contains the common variations among the individual tree core series and retains low-through high-frequency common variance, presumably in response to climate (Cook 1985).
2.3 Meteorological data and statistical analysis
Tree-ring series were filtered into low-and high-frequency signals using Gaussian-weighted digital filters (LaMarche 1974). We used paired reciprocal filters to separate low-frequency variations greater than 8 years from high-frequency signals less than 8 years (Fritts 1976). To assess the growth controlling factors among the individual sites, the first principal components of tree-ring data were obtained through the principal component analyses (PCA) over the common period of the chronologies (1900–2008).
Climate data from the meteorological stations of Hezuo (data from 1958 to 2009), Maqu (data from 1967 to 2008), Wenxian (data from 1959 to 2008) and Zhouqu (data from 1972 to 2008) were employed to analyze the effects of climate on TRW and MXD at the different sites (Fig. 1). To provide a more regional climate signal, the gridded monthly climate data was also obtained from the Climatic Research Unit (CRU), East Anglia, UK (http://www.cru.uea.ac.uk) for the western Qinling Mountains and northeastern Tibetan Plateau (averaged over 33–35°N, 102–105°E). As the oldest weather station (Mingxian) in the region was established in 1937, we only used the CRU data from 1937 to 2008 in further analyses.
The relationships between tree-ring indices and the climatic data were analyzed using the program DENDROCLIM2002 (Biondi and Waikul 2004). As the growth of a tree may be affected not only by the climatic conditions of the current growing season but also by those of the previous growing season (Fritts 1976; Chen et al. 2010), both the previous and the current growing seasons were included in the climate response analysis. The climate data used for the analysis included monthly mean temperature and total monthly precipitation over a span of 15 months (previous July to current September). To investigate the common growth response in more detail, we conducted spatial correlations between first principal components (PC1) and the updated 0.5°× 0.5° gridded temperature of CRU TS3.1 (Climate Research Unit) for the period 1937–2008 by the use of the KNMI climate explorer (http://climexp.knmi.nl, Trouet and van Oldenborgh 2013).
3 Results
3.1 The characteristics of tree-ring chronologies
Table 2 gives the general statistics of the tree-ring chronologies from COFECHA and ARSTAN. The mean correlation of the individual cores (with the master series) ranged from 0.42 to 0.55. The highest mean correlation was found for TRW of site TLD and the lowest one is for MXD of site ZC. The high correlation indicates good cross dating between sequences. The first-order autocorrelation ranged from 0.18 to 0.74. TRW had higher first-order autocorrelations than MXD. This implies that MXDs had lower sensitivities to previous year’s conditions than TRW.
| Table 2. Descriptive statistics for the standard tree-ring chronologies in the western Qinling Mountains and northeastern Tibetan Plateau. TRW: tree-ring width; MXD: maximum latewood density; MS: the mean sensitivity; AC1: the AutoCorrelation order 1; SD: the standard deviation; SNR: the signal-to noise ratio; PC1: the first principal components; EPS: the expressed population signal. | ||||||||||
| Site | Type of parameter | Time span | MS | SD | SNR | AC1 | R | EPS | PC1 | EPS > 0.85, ≥5 series |
| LLG | TRW | 1598–2006 | 0.12 | 0.24 | 17.27 | 0.74 | 0.50 | 0.95 | 30.0 | 1650 |
| TLD | TRW | 1737–2006 | 0.13 | 0.19 | 21.41 | 0.66 | 0.55 | 0.96 | 31.3 | 1770 |
| ZC | TRW | 1650–2006 | 0.11 | 0.16 | 11.13 | 0.58 | 0.52 | 0.92 | 32.1 | 1685 |
| GGS | TRW | 1603–2008 | 0.12 | 0.21 | 6.63 | 0.66 | 0.47 | 0.87 | 33.6 | 1635 |
| ZC | MXD | 1667–2008 | 0.05 | 0.05 | 6.77 | 0.28 | 0.42 | 0.87 | 26.6 | 1720 |
| GGS | MXD | 1625–2008 | 0.04 | 0.05 | 3.32 | 0.40 | 0.51 | 0.85 | 38.6 | 1685 |
| NQG | MXD | 1603–2008 | 0.07 | 0.07 | 7.26 | 0.18 | 0.54 | 0.88 | 38.5 | 1650 |
TRW chronologies exhibit relatively low mean sensitivities (MS, 0.11–0.13) and standard deviations (SD, 0.16–0.24). These data indicate rather moderate interannual variations in the ring-width series. The expressed population signal (EPS, 0.87–0.96) and variances in the first eigenvector (VFE, 26.6–38.6%) indicate that the growth of different trees were responding to common factors. The MXD chronologies had lower signal-to-noise ratio (SNR) and EPS than TRW chronologies. The MXD indices exhibit low year-to-year variability, as emphasized by the low mean sensitivities (0.05–0.07) and the standard deviations (0.04–0.07).
3.2 Cross-correlations of tree-ring series
Site chronologies for the common time interval 1900–2008 were established for the five sites, and showed different growth patterns (Fig. 3). The cross correlations in Table 3 show highly significant similarities among the chronologies. Virtually all of the coefficients between TRW chronologies were positively significant. The three MXD chronologies also display significant inter-site correlations. The cross-correlations among TRW chronologies were higher at the low-frequency band, while the MXD of the GGS site was highly correlated with the MXD of other two sites (NQG and ZC) at the high-frequency band. Principal component analyses revealed that the first principal components of the TRW chronologies (PC1TRW) and the MXD chronologies (PC1MXD) have eigen values >1.5 and account for 54.71% and 59.56% of the total variance, respectively.
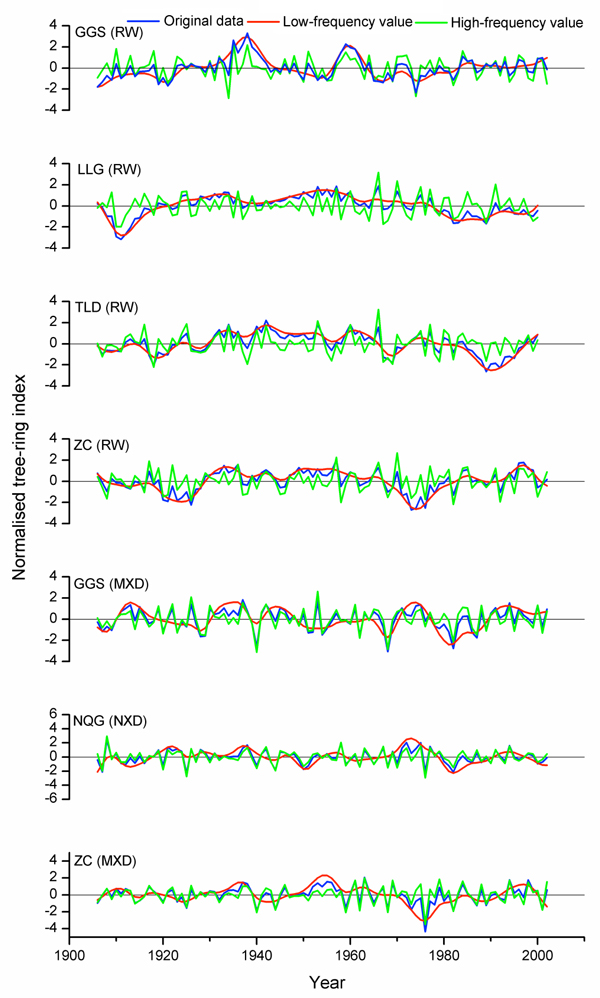
Fig. 3. Tree-ring chronologies of Faxon fir (1900–2008) from the five study sites. TRW: tree-ring width; MXD: maximum latewood density.
| Table 3. Cross-correlations for tree-ring indices before and after filtering during the common period (1900–2008). TRW: tree-ring width; MXD: maximum latewood density. | ||||||
| Site | GGS (TRW) | LLG (TRW) | TLD (TRW) | ZC (TRW) | GGS(MXD) | NQ (MXD) |
| Unfiltered signals | ||||||
| LLG (TRW) | 0.39** | |||||
| TLD (TRW) | 0.51** | 0.51** | ||||
| ZC (TRW) | 0.46** | 0.26** | 0.22 | |||
| GGS (MXD) | 0.29** | 0.08 | 0.17 | 0.14 | ||
| NQ (MXD) | –0.23* | 0.00 | 0.12 | 0.16 | 0.32** | |
| ZC (MXD) | 0.07 | 0.03 | 0.11 | 0.40** | 0.38** | 0.48** |
| Low frequency | ||||||
| LLG (TRW) | 0.20* | 1.00 | ||||
| TLD (RW) | 0.36** | 0.55** | ||||
| ZC (TRW) | 0.40** | 0.21* | 0.27** | |||
| GGS (MXD) | 0.23* | 0.00 | 0.16 | 0.01 | ||
| NQ (MXD) | 0.10 | 0.34** | 0.02 | –0.41** | 0.41** | |
| ZC (MXD) | 0.26* | 0.20 | 0.11 | 0.73** | 0.02 | 0.12 |
| High frequency | ||||||
| LLG (TRW) | 0.16 | 1.00 | ||||
| TLD (TRW) | 0.06 | 0.57** | 1.00 | |||
| ZC (TRW) | 0.02 | 0.52** | 0.37** | 1.00 | ||
| GGS (MXD) | 0.02 | 0.20* | 0.24* | 0.29** | 1.00 | |
| NQ (MXD) | 0.03 | 0.05 | 0.10 | 0.02 | 0.35** | 1.00 |
| ZC (MXD) | 0.04 | 0.01 | 0.06 | 0.19 | 0.57** | 0.66** |
| * p < 0.05; ** p < 0.01 | ||||||
3.3 Climate–growth response
Tree-ring width data show higher correlations with temperature than with precipitation (Fig. 4). The radial growth at the GGS site was positively correlated with July temperature. Significant positive correlations between the radial growth and temperature at the LLG site were found in July and September of the previous year, and in February, March, June and July of the current year. The radial growth at the TLD site was significantly correlated with the current growing season temperature (February, March, April, June and July), and with the previous summer and autumn temperature. Significant positive correlations between the radial growth at the ZC site and temperature were found in November of the previous year, and in June and August of the current year. Significant negative correlations between the radial growth and precipitation of the previous November are found at the GGS and ZC site. The June precipitation is also negatively correlated with the radial growth at the TLD site. The April precipitation is also negatively correlated with the radial growth at the ZC site.
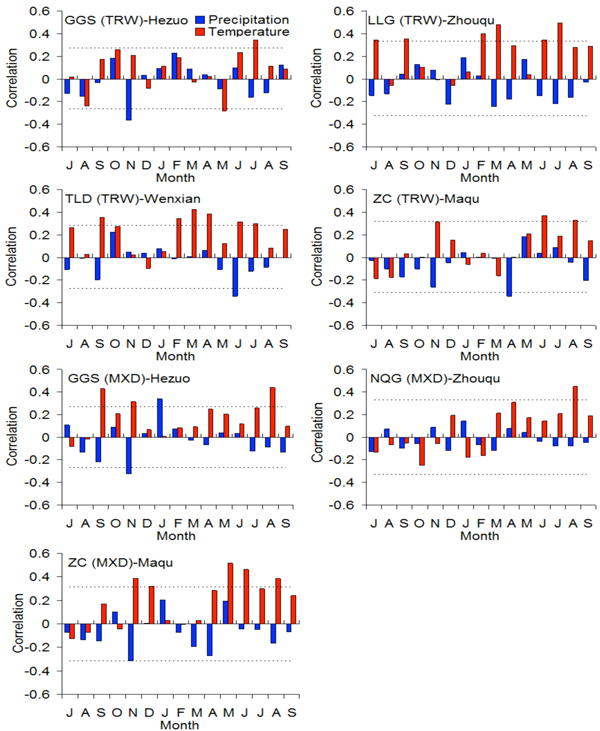
Fig. 4. Correlations of tree-ring chronologies of Faxon fir with climatic characteristics in the western Qinling Mountains and northeastern Tibetan Plateau, obtained from simple correlations (bars). The dot lines indicate significant variables (P < 0.05). TRW: tree-ring width; MXD: maximum latewood density.
The MXD chronologies at the three sites show similar responses to temperature during the warm season. We found strong positive correlations between MXD and temperature during the warm season. However, the effective months differ among the sites: the MXD of the GGS site is positively correlated with temperatures of the previous September and November, and July-August of the current year; the MXD of the NQG site is positively correlated with August temperature; the MXD of the ZC site is positively correlated with temperatures of the previous November-December and May-August of the current year. The MXD of the ZC and GGS site are negatively correlated with the precipitation of the previous November.
The results of the response function and correlation analyses reveal that the PC1TRW is related mainly to June–August temperature (p < 0.01) (Fig. 5). Strong positive relationships (p < 0.05) of the PC1TRW with summer (July) and autumn (September and October) of the previous year and early spring (March) temperature are also found. The PC1TRW has a strong negative relationship with June precipitation. We found strong positive correlations between PC1MXD and summer temperature (July-August), whereas the PC1MXD is negatively correlated with March and August precipitation.
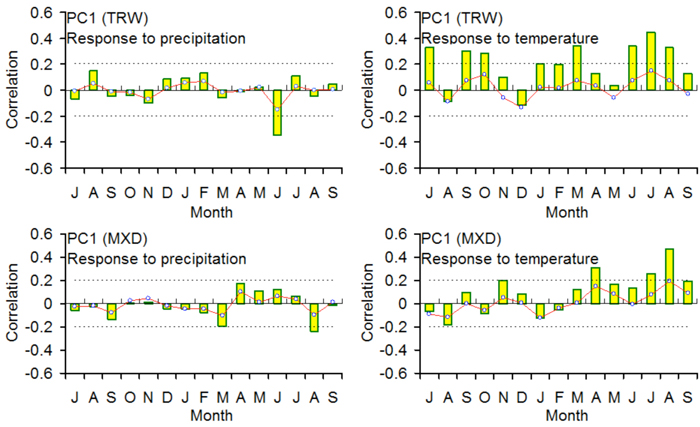
Fig. 5. The bootstrapped response (lines) and correlation (bars) functions of the first principal components of the TRW chronologies (PC1TRW) and the MXD chronologies (PC1MXD) with the monthly sum of precipitation and the monthly mean temperature from previous July to current September (1937–2008). The dotted lines indicate significance levels (p < 0.05). TRW: tree-ring width; MXD: maximum latewood density.
We screened PC1TRW and PC1MXD in correlation analysis with the seasonal combinations of temperature and precipitation of CRU (1937–2008) from previous July to current September. The strongest correlation was found between PC1MXD and August temperature (r = 0.45, p < 0.01), while PC1TRW displayed highest positive correlations with June–August temperature (r = 0.49, p < 0.01). The results of spatial correlation analysis show that the PC1 of TRW and MXD correlate > 0.4 with temperature grid data in a large area of Central China (Fig. 6). Despite a complex mountain terrain and spatial differences in local temperature and tree-ring growth, based on the above analysis results, temperature is the most important controlling factor on Faxon fir growth in the western Qinling Mountains and northeastern Tibetan Plateau.
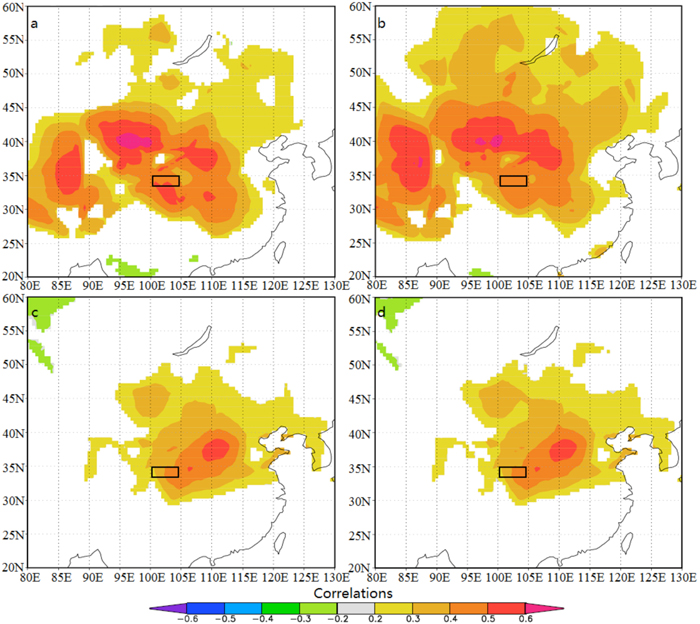
Fig. 6. (a) Spatial correlations between the gridded June–August temperature (CRU TS3.1) and the first principal component of the TRW chronologies (PC1TRW) for the period 1937–2008. (b) Spatial correlations between the gridded June–August temperature (CRU TS3.1) and the detrended PC1TRW. (c) Spatial correlations between the gridded August temperature (CRU TS3.1) and the first principal component of the MXD chronologies (PC1MXD). (d) Spatial correlations between the gridded August temperature (CRU TS3.1) and the detrended PC1MXD for the period 1937–2008.
PC1TRW showed significant increase in the radial growth under the global warming of 20th century, and captured the warming trends and allowed detecting the most recent warming in a long-term context (Fig. 7a). The divergence phenomenon was also observed in our study area during the period 1970–1980 (Fig. 7d). The MXD of Faxon fir did not clearly lose its temperature sensitivity in our study areas (Fig. 7b, c), while there is no upward trend in PC1MXD.
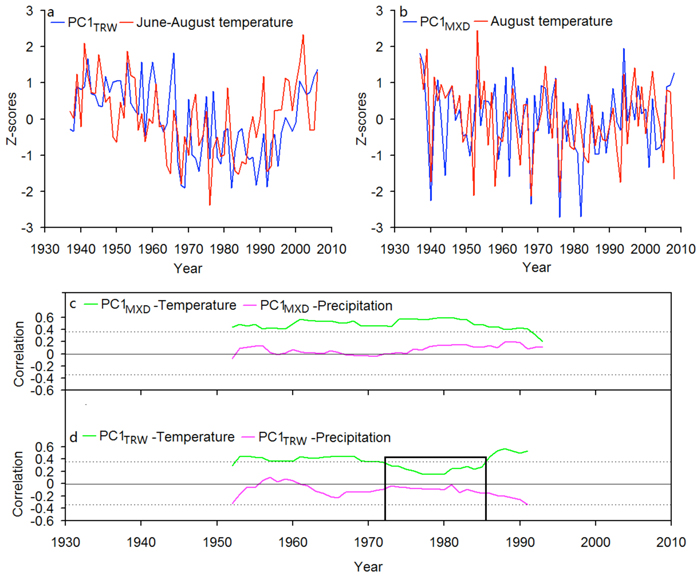
Fig. 7. (a) Comparison between the first principal component of the TRW chronologies (PC1TRW) and June–August temperature. (b) Comparison between the first principal component of the MXD chronologies (PC1MXD) and August temperature. (c) Running 31-year correlation between PC1MXD and August temperature. (d) Running 31-year correlation between PC1TRW and June–August temperature. TRW: tree-ring width; MXD: maximum latewood density.
4 Discussion
4.1 Climate–growth relationships at the sampling sites
The radial growth of Faxon fir at the timberline in our study area is highly correlated with temperature, rather than with precipitation. At the high elevation sites (TLD and LLG), temperature in March may be sufficiently warm to melt the winter snow cover, improving soil moisture and initiating an early growing season, as indicated by the positive correlations between ring widths and temperature in the month prior to the growing season (Fig. 5). In addition, higher early spring temperature might advance the beginning of the growing season. The positive correlations between PC1TRW and the summer temperature suggest that the radial growth of Faxon fir at the timberlines in the western Qinling Mountains and northeastern Tibetan Plateau is accelerated by high temperature in summer. The climate of this region is strongly influenced by Asian summer monsoon. The windward slopes of study areas can receive adequate rainfall in the monsoon season. Although summer is the hottest season of the year, moisture stress is no longer a problem because of the beginning of monsoonal rains. Therefore, tree-ring widths of the species studied in our study area are suggested to respond mainly to temperature. Warm temperature can lead to high radial growth at the timberline. In contrast, high negative correlation was found between June precipitation and PC1TRW. Enhanced precipitation may lead to related reduced temperature (Bräuning and Mantwill 2004). The cloud cover also decreases light energy, which in turn brings about a reduction in the photosynthetic production of plants (Takahashi et al. 2005, 2011). Moreover, at the colder ZC and GGS site, lower winter and early spring temperatures accompanied by winter snowpack might delay the beginning of the growing season, resulting in negative correlations of the radial growth of Faxon fir with November and April precipitation (Fang et al. 2009). To sum up, the radial growth of Faxon fir in the western Qinling Mountains and northeastern Tibetan Plateau is mainly controlled by the temperature variations, while higher precipitation could result in decreased temperature, leading to significantly negative correlations between the radial growth of Faxon fir and precipitation.
Similar to PC1TRW, high positive correlation (p < 0.001) was found between PC1MXD and summer temperature. Maximum latewood density is an annual ring parameter based on the highest density of the cells formed at the end of the growing season (Parker and Jozsa 1973). Even though cell division ceases at the end of the growing season, the thickening of cell walls of tracheids continues. The climate of late growth season may directly affect the thickening of cell walls of the last formed cells (Parker and Jozsa 1973). The values of MXD are mainly limited by the cold temperature of the late growing season. Thus, it appears that the period of maturation of the last formed cells corresponds to the months that yield significant correlations between MXD and late temperature (August). In addition, the growth of trees may be affected not only by the current climatic conditions of but also by those of the early part of the growing season. The climate of the early part of the growing season also has a significant impact on the formation of MXD. The strong correlations of MXD with temperature during the early vegetation period are also reported from the northern latitudinal timberline and the high-elevation sites of Eurasia (Wang et al. 2001; Briffa et al. 2002; Bräuning and Mantwill 2004; Frank and Esper 2005; Büntgen et al. 2006). In addition, MXD also showed the negative correlation with August precipitation. Wet and cold climatic conditions strongly depress the growth of latewood.
4.2 Tree-ring growth and twentieth century warming
The tree-ring data in temperature sensitive regions of the middle and high latitude Asia, southwestern China and Tibetan Plateau, including our study area have revealed the twentieth century warming trend (Jacoby et al. 1996; Gou et al. 2007; Fan et al. 2008; Liang et al. 2009). However, we found the relationship between PC1TRW and June-August temperature to be weak and instable over time, and tree-ring growth rate that does not parallel the increase in temperature in the recent years. D’Arrigo et al. (2008) have suggested that temperature beyond a warming-induced threshold may negatively influence growth, largely due to decreasing net photosynthetic gains and temperature-induced drought stress. This phenomenon was also observed in our study area (Fig. 7d). Although tree-ring growth trend is similar to the warming trend during the period 1990–2008, caution is advised, as the correlations between PC1TRW and temperature during the late 20th century might be inflated by this upward trend.
As described above, PC1MXD likely reflect climate conditions during a relatively short part of the growth season when compared with PC1TRW. Our analyses also confirmed a strong relationship between PC1MXD and August temperature across the network over the twentieth century (Fig. 7b). As shown in Fig. 7, however, PC1TRW has a upward trend and two prominent peaks in 1940s and most recent years, and strong low-frequency signals were found in PC1TRW. The divergences between PC1TRW and PC1MXD may be caused by the physiological processes. The radial growth was not only affect by the climate conditions of the current growing season, but also influence by the growth and the climate conditions of previous years (Fritts 1976). In contrast, latewood thickening is mainly limited by the temperature of the later part of the current growing season (Wang et al. 2001). Moreover, in both major IPCC assessments of climate change, the warming trend is greater in winter and spring than in summer (Houghton et al. 1996; IPCC 2007). Despite high correlation (r = 0.72, p < 0.001), June-August showed significant low-frequency variability, and August showed significant high-frequency variability. The divergent response of PC1TRW and PC1MXD to warming trends may also be linked with the seasonal variation of warming trends. In an attempt to test correlations, we therefore suggest to perform careful site selection over split periods of long instrumental measurements, validate the obtained signal over independent periods, and use appropriate tree-ring parameters that retain the true climate signals.
5 Conclusions
We have developed TRW and MXD chronologies of Faxon fir at the timberline sites in the western Qinling Mountains and northeastern Tibetan Plateau, China. The cross-matching statistics between trees for each parameter are relatively high. The climate response analysis shows that the MXD of Faxon fir can potentially be exploited as an indicator for dendroclimatological studies because of its strong responses to summer temperature. Tree-ring width series were strongly correlated with June-August temperature. Our present results confirm the potential utility of maximum latewood density and ring width of Faxon fir in the western Qinling Mountains and northeastern Tibetan Plateau as proxy for temperature reconstructions. The variations of tree-ring parameters under twentieth century warming were also assessed. Correlations with the temperature indicated sensitivity for MXD, but less spatiotemporal stability for TRW. The divergent response of between PC1TRW and PC1MXD to warming trends is possibly related to (i) regional climatic/environmental conditions, (ii) differences in physiological processes, and (iii) seasonal variation of warming trends. Although our data provide some evidence of possible tree-ring growth change as a result of twentieth century warming at timberline sites of the western Qinling Mountains and northeastern Tibetan Plateau, the role of most recent global warming and seasonal variations of warming trends on local tree-ring growth needs further research.
Acknowledgments
This work was supported by supported by The Basic Research Operating Expenses of the Central-level Non-profit Research Institutes (IDM201105), NSFC Project (41375122 and 41405081), the National Basic Research Program of China (2012CB955301). We thank the reviewers whose comments greatly benefitted this manuscript.
References
Biondi F., Waikul K. (2004). DENDROCLIM2002: a C++ program for statistical calibration of climate signals in tree-ring chronologies. Computers & Geosciences 30: 303–311. http://dx.doi.org/10.1016/j.cageo.2003.11.004.
Bräuning A., Mantwill B. (2004). Summer temperature and summer monsoon history on the Tibetan plateau during the last 400 years recorded by tree rings. Geophysical Research Letters 31: L24205. http://dx.doi.org/10.1029/2004GL020793.
Briffa K.R., Schweingruber F., Jones P., Osborn T., Shiyatov S.G., Vaganov E.A. (1998). Reduced sensitivity of recent tree growth to temperature at high northern latitudes. Nature 391: 678–682. http://dx.doi.org/10.1038/35596.
Briffa K.R., Osborn T.J., Schweingruber F.H., Jones P.D., Shiyatov S.G., Vaganov E.A. (2002). Tree-ring width and density around the Northern Hemisphere: part 1, local and regional climate signals. The Holocene 12:737–757. http://dx.doi.org/10.1191/0959683602hl587rp.
Buckley B.M., Cook E.R., Peterson M.J., Barbetti M. (1997). A changing temperature response with elevation for Lagarostrobos franklinii in Tasmania, Australia. Climatic Change 36: 477–498.
Büntgen U., Frank D.C., Nievergelt D., Esper J. (2006). Summer temperature variations in the European Alps, AD 755–2004. Journal of Climate 19: 5606–5623. http://dx.doi.org/10.1175/JCLI3917.1.
Büntgen U., Frank D., Trouet V., Esper J. (2010). Diverse climate sensitivity of Mediterranean tree-ring width and density. Trees 24: 261–273. http://dx.doi.org/10.1007/s00468-009-0396-y.
Chen F., Yuan Y.J., Wei W.S., Yu S.L., Li Y., Zhang R.B., Zhang T.W., Shang H.M. (2010). Chronology development and climate response analysis of Schrenk spruce (Picea Schrenkiana) tree-ring parameters in the Urumqi river basin, China. Geochrinometria 36: 17–22. http://dx.doi.org/10.2478/v10003-010-0014-4.
Cleaveland M.K. (1986). Climatic response of densitometric properties in semiarid site tree rings. Tree-Ring Bulletin 46: 13–47.
Cook E.R. (1985). A time-series analysis approach to tree-ring standardization. PhD dissertation, The University of Arizona, Tucson.
Cook E.R., Kairiukstis L.A. (1990). Methods of dendrochronology: applications in the environmental sciences. Kluwer, Dordrecht. 394 p. http://dx.doi.org/10.1007/978-94-015-7879-0.
D’Arrigo R., Kaufmann R., Davi N., Jacoby G., Laskowski C., Myneni R., Cherubini P. (2004). Thresholds for warming-induced growth decline at elevational treeline in the Yukon Territory. Global Biogeochemical Cycles 18: GB3021. http://dx.doi.org/10.1029/2004GB002249.
D’Arrigo R., Wilson R., Liepert B., Cherubini P. (2008). On the ‘divergence problem’ in northern forests: a review of tree-ring evidence and possible causes. Global and Planetary Change 60: 289–305. http://dx.doi.org/10.1016/j.gloplacha.2007.03.004.
Driscoll W., Wiles G., D’Arrigo R., Wilmking M. (2005). Divergent tree growth response to recent climatic warming, Lake Clark National Park and Preserve, Alaska. Geophysical Research Letters 32: L20703. http://dx.doi.org/10.1029/2005GL024258.
Eschbach W., Nogler P., Schär E., Schweingruber F.H. (1995). Technical advances in the radiodensitometrical determination of wood density. Dendrochronologia 13: 155–168.
Esper J., Frank D., Büntgen U., Verstege A., Hantemirov R.M., Kirdyanov A. (2010). Trends and uncertainties in Siberian indicators of 20th century warming. Global Change Biology 16: 386–398. http://dx.doi.org/10.1111/j.1365-2486.2009.01913.x.
Ettl G.J., Peterson D.L. (1995). Growth response of subalpine fir (Abies lasiocarpa) to climate in the Olympic Mountains, Washington, DC, USA. Global Change Biology 1: 213–230. http://dx.doi.org/10.1111/j.1365-2486.1995.tb00023.x.
Fan Z.X., Bräuning A., Cao K.F. (2008). Annual temperature reconstruction in the central Hengduan Mountains, China, as deduced from tree rings. Dendrochronologia 26: 97–107. http://dx.doi.org/10.1016/j.dendro.2008.01.003.
Fan Z.X., Bräuning A., Yang B., Cao K.F. (2009). Tree ring density-based summer temperature reconstruction for the central Hengduan Mountains in southern China. Global and Planetary Change 65: 1–11. http://dx.doi.org/10.1016/j.gloplacha.2008.10.001.
Fang K.Y., Gou X.H., Chen, F.H., Peng J.F., D’Arrigo R., Wright W., Li M.H. (2009). Response of regional tree-line forests to climate change: evidence from the northeastern Tibetan Plateau. Trees 23: 1321–1329. http://dx.doi.org/10.1007/s00468-009-0373-5.
Frank D., Esper J. (2005). Characterization and climate response patterns of a high elevation, multi species tree-ring network for the European Alps. Dendrochronologia 22: 107–121. http://dx.doi.org/10.1016/j.dendro.2005.02.004.
Fritts H.C. (1976). Tree ring and climate. Academic Press, London, 567 p.
Garfin G.M., Hughes M.K., Liu Y., Burns J.M., Touchan R., Leavitt S.W., An Z.S. (2005). Exploratory temperature and precipitation reconstructions from the Qinling Mountains, Northcentral China. Tree-ring Research 61: 59–72. http://dx.doi.org/10.3959/1536-1098-61.2.59.
Gou X., Chen F., Jacoby G.C., Cook E.R., Yang M.X., Peng J.F., Zhang Y. (2007). Rapid tree growth with respect to the last 400 years in response to climate warming, northeastern Tibetan Plateau. International Journal of Climatology 27: 1497–1503. http://dx.doi.org/10.1002/joc.1480.
Holmes R.L. (1983). Computer-assisted quality control in tree-ring dating and measurement. Tree Ring Bulletin 43: 69–95.
Hughes M.K., Wu X.D., Shao X.M., Garfin G.M. (1994). A preliminary reconstruction of rainfall in central China since A.D., 1600 from tree-ring density and width. Quaternary Research 42: 88–99. http://dx.doi.org/10.1006/qres.1994.1056.
Houghton J.T., Meira Filho L.G., Callander B.A., Harl-is N., Kattenberg A., Maskell K. (1996). Climate change 1995: the science of climate change. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 572 p.
IPCC. (2007). Fourth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
Jacoby G.C., D’Arrigo R.D., Davaajamts T. (1996). Mongolian tree rings and 20th century warming. Science 273:771–773. http://dx.doi.org/10.1126/science.273.5276.771.
Jacoby G.C., Lovelius N., Shumilov O., Raspopov O., Kurbainov J., Frank D. (2000). Long-term temperature trends and tree growth in the Taymir region of northern Siberia. Quaternary Research 53: 312–318. http://dx.doi.org/10.1006/qres.2000.2130.
LaMarche V.C. (1974). Frequency-dependent relationships between tree-ring series along an ecological gradient and some dendroclimatic implications. Tree-ring Bulletin 34:1–20.
Liang E.Y., Shao X.M., Xu Y. (2009). Tree-ring evidence of recent abnormal warming on the southeast Tibetan Plateau. Theoretical and Applied Climatology 98: 9–18. http://dx.doi.org/10.1007/s00704-008-0085-6.
Liu Y., Linderholm H.W., Song H.M., Cai Q.F., Tian Q.H., Sun J.Y., Chen D.L., Simelton E., Seftigen K., Tian H., Wang R., Bao G., An Z.S. (2008). Temperature variations recorded in Pinus tabulaeformis tree rings from the southern and northern slopes of the central Qinling Mountains, central China. Boreas 38: 285–291. http://dx.doi.org/10.1111/j.1502-3885.2008.00065.x.
Lloyd A.H., Fastie C.L. (2002). Spatial and temporal variability in the growth and climate response of treeline trees in Alaska. Climatic Change 52: 481–509. http://dx.doi.org/10.1023/A:1014278819094.
Parker M.L., Jozsa L.A. (1973). X-ray scanning machine for tree-ring width and density analysis. Wood Fiber 5: 192–197.
Peterson D.W., Peterson D.L. (2001). Mountain hemlock growth responds to climatic variability at annual and decadal time scales. Ecology 82: 3330–3345. http://dx.doi.org/10.1890/0012-9658(2001)082[3330:MHGRTC]2.0.CO;2.
Osborn T.J., Briffa K.R., Jones P.D. (1997). Adjusting variance for sample-size in tree-ring chronologies and other regional mean timeseries. Dendrochronologia 15: 89–99.
Schweingruber F.H., Fritts H.C., Bräker O.U., Drew L.G., Schär E. (1978). The X-ray technique as applied to dendroclimatology. Tree-ring Bulletin 38: 61–91.
Solberg B.O., Hofgaard A., Hytteborn H. (2002). Shifts in radial growth responses of coastal Picea abies induced by climatic change during the 20th century, central Norway. Ecoscience 9: 79–88.
Stokes M.A., Smiley T.L. (1968). An introduction to tree ring dating. The University of Chicago Press, Chicago, 73 p.
Takahashi K., Tokumitsu Y., Yasue K. (2005). Climatic factors affecting the tree-ring width of Betula ermanii at the timberline on Mount Norikura, central Japan. Ecological Research 20: 445–451. http://dx.doi.org/10.1007/s11284-005-0060-y.
Takahashi K., Okuhara I., Tokumitsu Y., Yasue K. (2011). Responses to climate by tree-ring widths and maximum latewood densities of two Abies species at upper and lower altitudinal distribution limits in central Japan. Trees 25: 745–753. http://dx.doi.org/10.1007/s00468-011-0552-z.
Trouet V., van Oldenborgh G.J. (2013). KNMI Climate Explorer: a web-based research tool for high-resolution paleoclimatology. Tree-Ring Reseach 69: 3–13. http://dx.doi.org/10.3959/1536-1098-69.1.3.
Wang H., Chen F., Yuan Y.J., Yu S.L., Shang H.M., Zhang T.W. (2013). Temperature signals in tree-ring width chronologies of alpine treeline conifers from the Baishui River Nature Reserve, China. Terrestrial, Atmospheric and Oceanic Sciences 24: 887–898. http://dx.doi.org/10.3319/TAO.2013.06.18.01(A).
Wang L.L., Payette S., Bégin Y., (2001). Tree-ring width and density characteristics of living, dead and subfossil black spruce at treeline in arctic Québec. The Holocene 11: 333–341. http://dx.doi.org/10.1191/095968301674769686.
Wang L.L., Duan J.P., Chen J., Huang L., Shao X.M. (2009). Temperature reconstruction from tree-ring maximum density of Balfour spruce in eastern Tibet, China. International Journal of Climatology 30: 972–979. http://dx.doi.org/10.1002/joc.2000.
Wigley T., Briffa K.R., Jones P.D. (1984). On the average value of correlated time series, with applications in dendroclimatology and hydrometeorology. Journal of Climate and Applied Meteorology 23: 201–213. http://dx.doi.org/10.1175/1520-0450(1984)023<0201:OTAVOC>2.0.CO;2.
Wilmking M., Myers-Smith I. (2008). Changing climate sensitivity of black spruce in a peatland-forest landscape in interior Alaska. Dendrochronologia 25: 167–175. http://dx.doi.org/10.1016/j.dendro.2007.04.003.
Wilmking M., D’Arrigo R., Jacoby G., Juday G. (2005). Divergent growth responses in circumpolar boreal forests. Geophysical Research Letters 32: L15715. http://dx.doi.org/10.1029/2005GL023331.
Zheng D. (1996). The system of physico-geographical region of the Qinghai-Xizang (Tibet) Plateau. Science in China Series D 39:410–417.
Total of 50 references

