Influence of water and nutrients on cork oak radial growth – looking for an efficient fertirrigation regime
Camilo-Alves C., Nunes J. A., Poeiras A. P., Ribeiro J., Dinis C., Barroso J. M., Vaz M., Almeida-Ribeiro N. (2022). Influence of water and nutrients on cork oak radial growth – looking for an efficient fertirrigation regime. Silva Fennica vol. 56 no. 3 article id 10698. https://doi.org/10.14214/sf.10698
Highlights
- Different summer fertirrigation treatments were tested on cork oaks over four years in a 1 ha plot
- Radial growth, meteorological parameters and fertirrigation volume were measured every 15–30 days
- During summer fertirrigated trees grew significantly more, independently of air vapor pressure deficit
- Increments were linearly related with fertirrigation volume up to 140 m3 week–1.
Abstract
The widespread cork oak (Quercus suber L.) mortality and reduced afforestation /regeneration are causing an overall reduction in cork production. To enhance trees’ growth and vitality, afforestation techniques using fertirrigation were tested. The main objective was the promotion of trees’ growth on new dense plantations using minimum water requirements until reaching productive forests. The experimental plot – Irricork – was installed in 2017 in a ≈1 ha stand with 14 years’ age cork oaks summer-fertirrigated since plantation. Four fertirrigation treatments were applied during fertirrigation campaigns. Radial growth, meteorological parameters and fertirrigation volume were measured every 15–30 days over four years. It was observed that weather, tree size, debarking and trees’ intra-competition had a significant effect on radial increments. Fertirrigation significantly enhanced growth during summer drought and decoupled increments from air vapor pressure deficit constraints. There was a linear relationship between trees’ radial increments and fertirrigation volume up to 140 m3 week–1. Above this value, increments were smoother. In conclusion, summer fertirrigation of 140 m3 week–1 efficiently enhanced the radial growth of trees with 50–75 circumference at breast height, under the particular edaphoclimatic conditions of the stand. This study showed to be, therefore, promising in the use of efficient fertirrigation the enhance cork oaks’ radial growth.
Keywords
irrigation;
mixed models;
Quercus suber;
climate–growth relationship;
increments;
stem radius
-
Camilo-Alves,
MED – Mediterranean Institute for Agriculture, Environment and Development & CHANGE – Global Change and Sustainability Institute, Institute for Advanced Studies and Research, University of Evora, Pólo da Mitra, Ap. 94, 7006-554 Évora, Portugal
 https://orcid.org/0000-0001-5156-172X
E-mail
calves@uevora.pt
https://orcid.org/0000-0001-5156-172X
E-mail
calves@uevora.pt

-
Nunes,
Department of Plant Science, School of Science and Technology, University of Evora, Pólo da Mitra, Ap. 94, 7006-554 Évora, Portugal
 https://orcid.org/0000-0002-6144-3484
E-mail
jain@uevora.pt
https://orcid.org/0000-0002-6144-3484
E-mail
jain@uevora.pt
-
Poeiras,
MED – Mediterranean Institute for Agriculture, Environment and Development & CHANGE – Global Change and Sustainability Institute, Institute for Advanced Studies and Research, University of Evora, Pólo da Mitra, Ap. 94, 7006-554 Évora, Portugal
 https://orcid.org/0000-0002-6049-807X
E-mail
apcp@uevora.pt
https://orcid.org/0000-0002-6049-807X
E-mail
apcp@uevora.pt
-
Ribeiro,
Department of Plant Science, School of Science and Technology, University of Evora, Pólo da Mitra, Ap. 94, 7006-554 Évora, Portugal
 https://orcid.org/0000-0001-7242-5866
E-mail
jmrpr@uevora.pt
https://orcid.org/0000-0001-7242-5866
E-mail
jmrpr@uevora.pt
-
Dinis,
 https://orcid.org/0000-0001-6984-1033
E-mail
dinis.cati@gmail.com
https://orcid.org/0000-0001-6984-1033
E-mail
dinis.cati@gmail.com
-
Barroso,
MED – Mediterranean Institute for Agriculture, Environment and Development & CHANGE – Global Change and Sustainability Institute, and Department of Plant Science, School of Science and Technology, University of Evora, Pólo da Mitra, Ap. 94, 7006-554 Évora, Portugal
 https://orcid.org/0000-0002-0160-3845
E-mail
jmmb@uevora.pt
https://orcid.org/0000-0002-0160-3845
E-mail
jmmb@uevora.pt
-
Vaz,
MED – Mediterranean Institute for Agriculture, Environment and Development & CHANGE – Global Change and Sustainability Institute, and Department of Biology, School of Science and Technology, University of Evora. Pólo da Mitra, Ap. 94, 7006-554 Évora, Portugal
 https://orcid.org/0000-0002-3368-757X
E-mail
mvaz@uevora.pt
https://orcid.org/0000-0002-3368-757X
E-mail
mvaz@uevora.pt
-
Almeida-Ribeiro,
ICT – Institute of Earth Sciences and Department of Plant Science, School of Science and Technology, University of Evora, Pólo da Mitra, Ap. 94, 7006-554 Évora, Portugal
 https://orcid.org/0000-0002-0160-3845
E-mail
nmcar@uevora.pt
https://orcid.org/0000-0002-0160-3845
E-mail
nmcar@uevora.pt
Received 17 January 2022 Accepted 14 July 2022 Published 20 September 2022
Views 63476
Available at https://doi.org/10.14214/sf.10698 | Download PDF

1 Introduction
Cork tissue or phellem is defined as the group of cells belonging to the periderm which derives from traumatic phellogen (Poeiras et al. 2021). Cork oaks (Quercus suber L.) have the capability to regenerate their cork after removal, not only making this species very unique but also allowing its product to be an eco-friendly and sustainable material. Cork can be removed every 9 or 10 years and around 17 times over the course of a tree’s lifetime. It is mostly used for stoppers (41.6% for natural cork stoppers, APCOR 2020). In addition to bottle stoppers, cork is used to make a wide range of products, including insulation panels, floors, wall tiles and sound-proofing in the car industry, as well as handicrafts and other artistic uses (FAO and Plan Bleu 2018). Cork is the most profitable product from Portuguese forests, representing 1.84% of Portuguese exports of goods, 1.25% of Gross Domestic Product and 1.86% of domestic employment (APCOR 2020). However, severe cork oak mortality events have been repeatedly occurring in its range area since the 1980s, disrupting the system in all its aspects (Macara 1975; Brasier 1992; Ferreira et al. 1992; Moreira and Martins 2005; Sousa et al. 2007; Camilo-Alves et al. 2013; Pinto-Correia and Godinho 2013). Trees loss is a result of several unfavorable conditions acting in synergism: permanent factors predisposing trees to decline – usually related to climatic constraints and soils with growth limitations that reduce site quality – acting together with temporary inciting factors such as inappropriate soil management and the presence of the pathogen Phytophthora cinnamomi Rands, are conducting the trees and the system to a widespread decline with loss of crown cover and lack of natural regeneration (Ribeiro and Surovy 2007; Ribeiro et al. 2008, 2011; Camilo-Alves et al. 2013; Ribeiro et al. 2014; Camilo-Alves et al. 2020b; Ritsche et al. 2021). Profound changes in stand management comprise relevant inciting factors to the degradation of cork oak woodlands. Those changes came from recent modifications in demography and agrarian policies: failure in negotiating European Union’s forestry integrated measures in the Common Agricultural Policy (CAP), specific agrarian measures considering cork woodland systems in a holistic management perspective, resulted in the partial financial measures addressed mainly to the agropastoral component. Private owners were led, therefore, to postpone regeneration of the forest component and to decide for the intensification of the agropastoral component in the cork oak woodland silvopastoral / agrosilvopastoral systems for short-term financial reasoning (Ribeiro et al. 2004, 2008, 2013; Pinto-Correia and Azeda 2017). All these constraints to natural and artificial regeneration, associated with a long time until gathering profitable cork from these slow-growing climax tree species – usually obtained after 40–50 years since plantation with the third debarking onwards – are also pushing private owners to opt for fast-growing trees, particularly Pinus pinea L. and the exotic Eucalyptus globulus Labill. (Costa et al. 2014) in afforestation events.
In 2003 a private farm owner decided to plant some cork oak seedlings on the edge of an olive grove, benefiting from its fertirrigation system. When the trees reached the proper size for the first debark – 70 cm in trunk perimeter at 130 height – with half of the expected age, the methodology attracted a great deal of interest in the cork sector. Particularly by the cork industry sector which had already detected an overall reduction in the quantity and quality of raw material. Private companies, farm owners and institutional research centers have then established several cooperation projects between them in order to develop afforestation techniques with efficient use of fertirrigation, considering water saving, the environmental impact and economic sustainability. The main objective of the projects is, therefore, the promotion of cork oak growth on new dense plantations using minimum water requirements until productive forests are reached. Constraints to the project are that new stands should be installed where access to water has no restrictions – for example, on the edge of irrigated cultures – and the installed forests should be able to grow and maintain their vitality under rainfed conditions. The first long-term scientific study on new cork oaks plantations with drip fertirrigation presented significant results on the establishment of the best water volume for young seedlings (Camilo-Alves et al. 2020a). In 2017 an experimental plot was installed in the stand with fertirrigated trees from the nearby olive grove, with 14–16 years age trees to date. Each plantation line was assigned to one fertirrigation treatment during fertirrigation campaigns and periodical measurements of the radial growth were associated with meteorological parameters and fertirrigation volume.
The aim of this study was to test the best fertirrigation volume that enhanced radial increments with the minimum water use in young trees, considering meteorological conditions. The specific objectives of this study are: 1- fertirrigation can influence trees’ response to the unfavorable meteorological conditions found in summer? 2 - How much fertirrigation is needed to improve cork oak radial growth?
2 Materials and methods
2.1 Study site
The study took place at “Herdade do Conqueiro” (39°03´N, 07°58´W), near Avis, Portugal. The region is characterized by a typical Mediterranean subhumid climate with hot and dry summers (Csa as the köppen-geiger climate classification for 1971–2000). The normal annual average for total rainfall in the region is 593 mm and for mean temperature is 16.3 °C (1971–2000, according to the Portuguese Institute for Sea and Atmosphere data for the nearest station). The 1.6-hectare with fertirrigated cork oaks was installed in 2003 on the extreme edge of an intensive olive grove, with a 7 × 3.5 m compass. Plants are being fertirrigated since its plantation in the same way as the adjacent olive grove, with a surface drip fertirrigation system. The farm is also covered by cork oak forest and, in this new cork oak plantation, there were already 13 centenary cork oak trees scattered around the stand. The terrain is flat and distant 50 m from “Barragem do Maranhão” reservoir. The soil was characterized as a Low Saturated Gleyic Luvisol. Soil profile evaluation and sampling were carried out in one location at three depths (Table 1).
| Table 1. Physical and chemical evaluation of the soil profile of a 1 ha fertirrigated cork oak plot in Avis, Portugal. | |||||
| Horizon depth (cm) | Organic Matter (%) | P2O5 (mg kg–1) | K2O (mg kg–1) | Total N (g kg–1) | texture |
| 10 | 3.39 | 86 | 350 | 5.60 | Loam |
| 80 | 0.63 | 7 | 94 | 0.40 | Sandy Clay loam |
| 180 | 0.22 | 5 | 60 | 0.30 | Sandy loam |
2.2 Stand characterization
The experimental plot – Irricork – was installed in 2017 and comprises ≈ 1 ha at the center of the stand, where 113 cork oaks are being monitored since that time (Fig. 1), excluding the centenary ones.
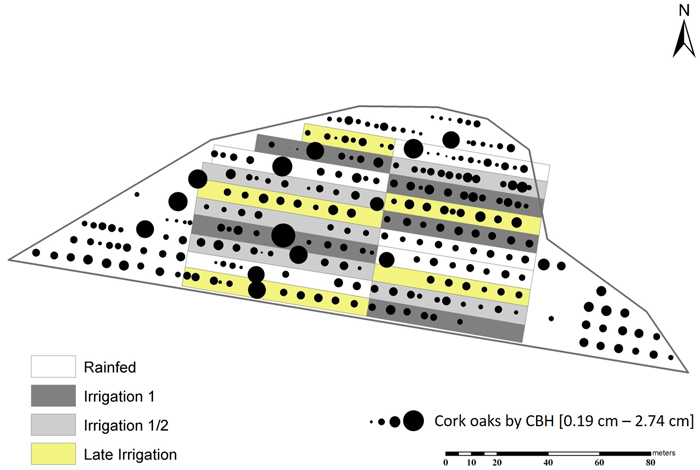
Fig. 1. Irricork: The 1 ha experimental cork oak plot divided by fertirrigation treatments, in Avis, Portugal.
Cork was debarked from 1 tree in 2011, from 7 trees in 2015 and 70 trees in early July 2017, leaving 35 cork oaks never debarked. All the cork oaks from the buffer and study site (a total of 260) were measured before treatments in February 2017 and repeatedly on an annual basis. Parameters measured were circumference at breast height (CBH), total height (TH), height to canopy basis (HCB) and four canopy radii (cp N E S W). Stand profile is in Table 2. Basal area of the stand is 10.58 m2 ha–1.
| Table 2. Results of the trees’ dendrometric measurement performed in 2017 at a 1 ha fertirrigated cork oak plot in Avis, Portugal. | |||||
| Trees | CBH (cm) | TH (m) | HCB (m) | canopy projection (m2) | |
| Planted in 2003/05 (mean + S.D.) | Debarked | 75.11 ± 11.04 | 9.26 ± 1.06 | 6.43 ± 0.45 | 20.33 ± 8.03 |
| Non-debarked | 52.05 ± 17.21 | 7.18 ± 1.76 | 4.79 ± 0.49 | 8.52 ± 5.88 | |
| centenary (N. 13) (mean + S.D.) | 214.16 ± 46.20 | 11.29 ± 1.10 | 7.88 ± 0.68 | 136.60 ± 56.87 | |
| CBH = trees’ circumference at breast height; TH = trees’ total height; HCB = trees’ height to canopy basis | |||||
2.3 Fertirrigation plot design
Fertirrigation was drip-surface with one tube per plantation line and 2.1 L drip emitters spaced 0.75 m apart. The study site corresponded to 0.92 ha in the center of the stand and the remaining belonged to the edge. The experimental plot was prepared to undergo three treatments plus control, each with five replicating blocks, randomly distributed throughout the study site (Fig. 1). Treatments were divided into:
- Fertirrigation 1 (F1) – the same water volume as the adjacent olive grove; roughly corresponding to a 5-hour day three times a week for a maximum of 210 m3 a week: however, frequency and duration could vary according to decisions of the landowner and following olive grove needs.
- Fertirrigation ½ (F½): half of the water volume of F1 (by covering half of the drippers).
- Late fertirrigation (LF): the same water volume of F1 but starting only in August.
- Rainfed (RF): No fertirrigation.
In 2017 and 2018, the blocks corresponding to F½ and LF were watered as F1. These treatments initiated only in 2019 (Fig. 2).
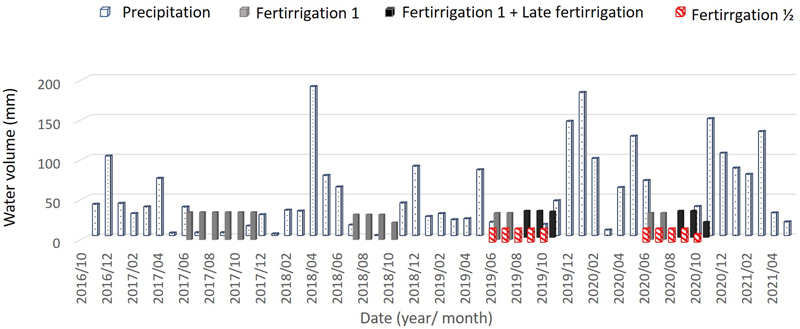
Fig. 2. Monthly volume of total water – Precipitation and irrigation – supplied to the cork oak plot in Avis, Portugal over the study period. In 2017 and 2018 “Late fertirrigation” and “Fertirrigation ½” treatments were watered as Fertirrigation 1.
Precipitation events defined the duration of each fertirrigation campaign. Dry springs or dry autumns resulted in, respectively, the anticipation and delay of the fertirrigation campaign. The experimental site had flowmeters at the entrance of each fertirrigation tube for better precision of the fertirrigation volume. It was possible to observe variations among the lines and over the weeks. Resume of water volume is in Table 3.
| Table 3. Resume of daily fertirrigation by treatment during fertirrigation campaign at a 1 ha fertirrigated cork oak plot in Avis, Portugal, between 2017 and 2020. | ||||
| Treatment | Daily fertirrigation (mm) | |||
| Mean | Maximum | Minimum | Standard Deviation | |
| Fertirrigation 1 | 1.29 | 2.91 | 0.01 | 0.78 |
| Fertirrigation ½ | 0.55 | 1.31 | 0.01 | 0.36 |
| Late Fertirrigation | 1.01 | 2.65 | 0.01 | 0.76 |
Fertilization: Inofert Plus (14:11:6 + 8B) was supplied in the irrigation water three times per fertirrigation campaign, for a total of (3.5 Kg. ha–1 year–1). All trees received foliar fertilization (Epson-combitop: MgO, SO3, Mn, Zn, 2 Kg. ha–1 year–1), regardless of watering treatments.
2.4 Data collection
2.4.1 Meteorological data
Daily precipitation (Prec) was measured with a udometer installed in the study site. Air temperature (aT), relative air humidity (raH), and solar irradiance (SI) measurements were obtained through IPMA (Portuguese Institute for Sea and Atmosphere) from the nearest station. Since spring 2019 a meteorological portable station was installed in the local. A data logger permanently gathered and store information every ten minutes about aT (°C), Prec (mm), raH (%) and SI (W m–2). Air vapor pressure deficit (VPD in Pa) was calculated with the following equation:
VPD = Saturated Vapor Pressure (ES) − Actual Vapor Pressure (EA), where:
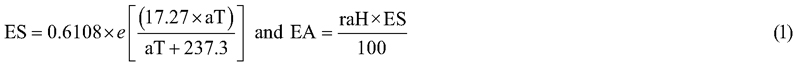
2.4.2 Measurements of the stem increments
After cork debark, in July 2017, 39 trees dispersed along the study site received band dendrometers in the trunk at 130 cm height, half of them on debarked trees and equally divided by treatments. In January 2019, a further 75 trees were added to this monitoring. Trees’ stem increment was measured monthly during winter and every two weeks during the rest of the year. As the periods between measurements – the time units (t–1 → t) – were not constant, the effect of the period size was removed by calculating the daily stem increment [(increment during each time unit / (n. days of the time unit)]. For the analyses, stem increment in radius was preferred instead of circumference or area for a better estimation of the effect of tree size (basal area) on growth.
2.4.3 Fertirrigation volume calculation
Fertirrigation volume (m3) was read on the flowmeters at the entrance of fertirrigation tubes in the same days of the measurements of stem increments. It was considered that each tube fertirrigated an area calculated as the distance of the tube and half of the distance between plantation lines (see Fig. 1).
2.4.4 Individual-tree intraspecific competition analyses
The intraspecific spatial competition model was selected and calculated according to Ribeiro et al. (2006). The competition index (H) used was a spatial-dependent size-ratio index based on relative crown position and size (Hegyi 1974):

where DBH = trees’ diameter at breast height (m); dist = distance between trees (m); j = competitor trees; i = subject tree (Hegyi 1974).
In order to determine the count and which trees are labeled as competitors, i. e. the maximum radius (MR) of influence around the subject tree, it was tested two search indexes (Biging and Dobbertin 1994), one based on point sampling and basal area factor (D2):
![]()
where DBH = tree’ diameter at breast height (cm); j = competitor trees; i = subject tree (Biging and Dobbertin 1994).
And the other based on competition light cone (H3):

where j = competitor trees; i = subject tree; HT= tree’ total height; HCB = tree’ height to canopy basis (Biging and Dobbertin 1994).
Resume of collected data and calculated parameters are in Table 4.
| Table 4. Resume of collected data and calculated parameters at a 1 ha fertirrigated cork oak plot in Avis, Portugal, between 2017 and 2020. | ||||||
| Variables | Collected data | Average values | Calculated parameters | Average values | Periodicity | |
| Dependent | Trees’ Radial increment at 130 cm height | (0.25 ± 0.21 mm) /15 days | 15–30 days | |||
| Independent | Meteorological | Average Air Relative Humidity (raH) | 71.35 ± 14.77 % | air vapor pressure deficit (VPD) | 1.39 ± 0.88 Kpa | |
| Average Air Temperature (aT) | 15.67 ± 5.60 °C | |||||
| Average Solar Irradiance (SI) | 179.26 ± 81.84 Wm–2 | |||||
| Sum of Precipitation (Prec) | (23 ± 31 mm)/15 days | |||||
| Treatment | Sum of Irrigation | (5.2 ± 7.6 mm)/15 days | ||||
| Subject conditions | Trees cork’ age | Virgin: 16.40 ± 1.02 years | ||||
| Secondary: 2.83 ± 1.30 years | annual | |||||
| Trees Circunference at Breast Height (CBH) | 0.81 ± 0.03 m | Tree Intraspecific Competition (index) | 0.15 ± 0.01 | |||
| Georreferencing | lat, long | initial | ||||
2.5 Statistical analysis
The average values of the environmental factors VPD, SI and the sum of Prec were calculated for each time unit (t–1 → t). Daily Prec was calculated by dividing the sum of Prec by the number of days within each time unit.
Statistical analyses were made using the SPSS v.25 software package (IBM Corp., Armonk, NY, USA). For the fertirrigation campaign period, non-parametric independent-samples tests were applied to analyze differences in stem increments from the fertirrigated and non-fertirrigated periods regarding its distribution (Wald-Wolfowitz Runs; Mann-Whitney U; Kolmogorov-Smirnov; Jonckheere-Terpstra for Ordered Alternatives), medians (Median Test) and range (Moses Test of Extreme Reaction).
In addition to meteorological variables, other factors were considered: a) initial CBH; b) cork’ age – equal to the trees’ age for virgin cork, and counting from the last cork debark for reproduction cork; c) cork type (virgin or secondary); d) individual-tree spatial competition indices; e) distance to the reservoir; f) treatments. Before statistical modeling, all variables were graphically explored regarding distribution patterns and outliers. Collinearity was tested using Pearson’s correlation coefficient. Curve estimation regression models were used to determine how the independent and dependent variables are related. For some nonlinear relationships (ex. quadratic, cubic) there are points where the tangential is flat and may change positive relationships to negative ones and vice-versa. Derivative of each function was used to infer the flat points.
Generalized Linear Mixed Models (G.L.M.M.) were applied to analyze if and how the tree’s stem increments with repeated measurements (the time unit) were related to the independent variables. The dependent variable was fitted with a gamma regression since increments are positive and skewed to larger values. All independent variables were tested as fixed parameters and repeated measurements by subject were the random variable. Various combinations of factors, interactions and covariance matrices were tested, choosing the best model based on the significance of each factor, its effect on the information criterion, and its predictive capacity by graphically comparing with the observed data. Variables were tested in a full model and in two sub-models for fertirrigated and non-fertirrigated trees during fertirrigation campaigns. The full model gives an overview of the influence of the factors over the entire year, which includes the period of intense growth, such as spring, and the limiting period, such as winter. The sub-models refer only to the fertirrigation campaign period. In exploratory analyses an interaction between the treatment and VPD factors was detected, therefore fertirrigated trees were separately analyzed from the non-fertirrigated trees. This approach helped in understanding the differences in trees’ response to meteorological conditions – in order to answer the first specific objective. The sub-model of the fertirrigated trees was also used to analyze the minimum amount of water necessary to favor growth – the second specific objective.
3 Results
3.1 Curve estimation for weather variables
Average temperature was the variable most associated with stem increments (R2 = 0.22, Table 5), adjusted with a cubic shape and positively related with growth at values between 7–20 °C. The other variables adjusted better to radial growth with a quadratic shape, indicating the non-linear relationship with the dependent variable. Regarding fertirrigation, curve estimation was also tested to help in the construction of the growth models (below); the cubic relationship fitted better, with stem increments responding positively to water volume between 0.15–3.14 mm day–1.
| Table 5. Best fitting model of the curve estimation procedure for the relationship between daily stem increment (cm) at 130 height for each environmental factor, measured in a 1 ha fertirrigated cork oak plot in Avis, Portugal, between 2017 and 2020. | |||||||
| Factors | Equation | M. Summary | Parameter estimates | Tangential ≥ 0 | |||
| R2 | p-value | b1 | b2 | b3 | |||
| Av. raH (%) | Quadratic | 0.16 | <0.001 | 0.050 | –4.2E-04 | ]-∞, 60.11%] | |
| Av. aT (°C) | Cubic | 0.22 | <0.001 | –0.207 | 0.020 | –4.9E-04 | [6.95–20.33] |
| Av. SI (Wm–2) | Quadratic | 0.19 | <0.001 | 2.2E-04 | 5.0E-06 | [–22.46, +∞[ | |
| Av. VPD (Kpa) | Quadratic | 0.20 | <0.001 | 0.004 | –0.001 | ]-∞, 2.05] | |
| D. Prec (mm) | Quadratic | 0.11 | <0.001 | –0.005 | 0.001 | [4.8, +∞[ | |
| Av. = Average; raH = relative air humidity; aT = air temperature; SI = solar irradiance; VPD = air vapor pressure deficit; Prec = precipitation; D. = Daily; M. = Model | |||||||
3.2 Fertirrigation campaign
Fertirrigation campaigns lasted 6 months in 2017 (from June to the end of November) and 3.3 months in 2018, beginning in July. In 2019 and 2020 started in June and lasted 5 and 4.3 months respectively. During each time unit, medians and distribution of daily stem increments were significantly different between fertirrigated and non-fertirrigated trees (p < 0.001 for all the non-parametric tests, Fig. 3), and their ranges were non-statistically different (p > 0.05).
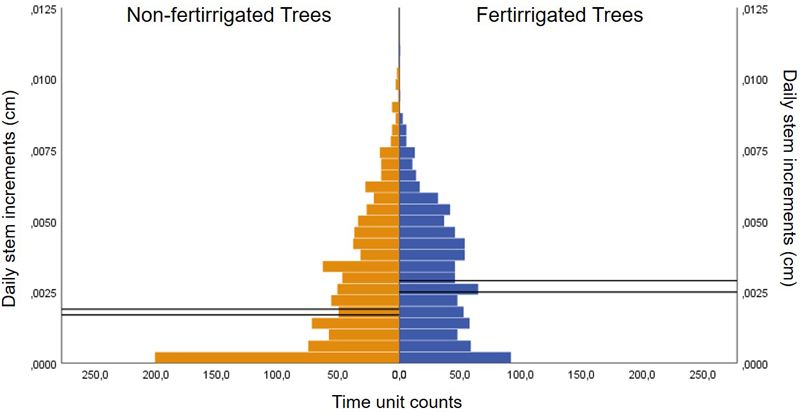
Fig. 3. Pyramid frequency (number of time units) of cork oak daily stem increments under fertirrigated and non-fertirrigated trees at a 1 ha cork oak plot in Avis, Portugal, during fertirrigation campaigns from 2017–2020. Solid lines represent confidence interval for the medians.
3.3 Growth models
3.3.1 Model 1: Full model for stem increments
The VPD was preferred instead of both aT and raH because of the high correction between them (Pearson coef. = –0.69). This factor was strongly associated with stem increments (F(VPD) = 417.40; F(VPD^2) = 444.04) followed by Prec (F(prec.) = 163.08; F(prec^2) = 24.66), SI (F = 143.94), fertirrigation (F(fi) = 32.45, F(fi^3) = 16.84) and intra-sp competition by means of competition light cone (F = 4.05) (Table 6). The curve of the precipitation (0.219 × Prec – 0.008 × Prec2) showed that the factor in the full model had a positive relationship with stem increments within its observed range (maximum estimated daily precipitation: 9.48 mm; flat point of the curve: 13.69 mm). The best covariance structure was the first-order autoregressive type where residual variance between trees and over time was significantly correlated (p < 0.001). The significance of the random effect covariance of the subject “tree” p = 0.041.
| Table 6.1. Generalized linear mixed model estimates of the Independent fixed effects on the daily stem increments (cm) at 130 height measured in a 1 ha fertirrigated cork oak plot in Avis, Portugal, between 2017 and 2020. | ||||||
| Model term | Coefficient | Std. Error | t-student | p-value | 95% Conf. Interval | |
| lower | upper | |||||
| Intercept | –11.117 | 0.208 | –53.351 | <0.001 | –10.708 | –11.525 |
| Cork age (year) | –0.052 | 0.005 | –10.608 | <0.001 | –0.042 | –0.062 |
| Initial CBH (cm) | 0.018 | 0.002 | 8.12 | <0.001 | 0.022 | 0.014 |
| Av. SI (Wm–2) | 0.006 | 0.001 | 11.923 | <0.001 | 0.007 | 0.005 |
| D. Prec (mm) | 0.231 | 0.018 | 13.086 | <0.001 | 0.266 | 0.196 |
| (Daily Prec)2 | –0.009 | 0.002 | –5.119 | <0.001 | –0.005 | –0.012 |
| Av. VPD (Kpa) | 2.588 | 0.129 | 20.093 | <0.001 | 2.841 | 2.336 |
| (Av. VPD)2 | –0.646 | 0.031 | –20.893 | <0.001 | –0.585 | –0.706 |
| D. fertirrigation | 0.218 | 0.037 | 5.93 | <0.001 | 0.291 | 0.146 |
| (D. fertirrigation)2 | 0.019 | 0.014 | 1.385 | 0.166 | 0.045 | –0.008 |
| (D. fertirrigation)3 | –0.018 | 0.004 | –4.966 | <0.001 | –0.011 | –0.025 |
| IC Hh3 | –0.395 | 0.163 | –2.428 | 0.015 | –0.714 | –0.076 |
| CBH = circumference at breast height; Av. = Average; SI: solar irradiance; Prec = precipitation; VPD = air vapor pressure deficit; D. = Daily; IC: Intra-competition; Hh3 = Hegyi Competition index based on competition light cone | ||||||
| Table 6.2. Generalized linear mixed model covariance estimates for residual and random effects (repetitions) with first-order autoregressive structure on the daily stem increments (cm) at 130 height measured in a 1 ha fertirrigated cork oak plot in Avis, Portugal, between 2017 and 2020. | ||||||
| Residual effect | Coefficient | Std. Error | Z-test | p-value | 95% Conf. Interval | |
| lower | upper | |||||
| AR1 Rho | 0.320 | 0.016 | 19.797 | <0.001 | 0.288 | 0.351 |
| AR1 Diagonal | 0.740 | 0.018 | 40.272 | <0.001 | 0.705 | 0.777 |
Stem increments were reduced over time in relation to corks’ age (F = 101.38) however, they were higher in larger trees (42.54). Trees’ competition by means of basal area factor, distance to the reservoir, and treatments effect were non-significant (p > 0.05). Variation over time was significant (p < 0.001) and positive. Residual variance in each period was also significant (p < 0.001) and larger than between periods, suggesting that most of the variability unaccounted for by the fixed effects was due to variation between trees.
3.3.2 Model 2: Fertirrigation campaign – non-fertirrigated trees
This model corresponded to the time units mainly occurring when precipitation was incipient, average temperatures were high and relative humidity was low. Stem increments from non-fertirrigated trees responded to weather variables during the fertirrigation campaign and were related to cork’ age (Table 7). The signal of intra-competition was not detected and distance to the reservoir was non-significant. The best covariance structure followed the same pattern found in the full model. The significance of the random effect covariance of the subject “tree” was p = 0.053.
| Table 7.1. Generalized linear mixed model estimates of the Independent fixed effects on the daily stem increments (cm) at 130 height measured on non-fertirrigated trees from a cork oak plot in Avis, Portugal, during the 2017–2020 Fertirrigation campaigns. | ||||||
| Model term | Coefficient | Std. Error | t-student | p-value | 95% Conf. Interval | |
| lower | upper | |||||
| Intercept | –4.237 | 0.53 | –7.988 | <0.001 | –3.196 | –5.279 |
| Cork age (year) | –0.052 | 0.007 | –7.038 | <0.002 | –0.038 | –0.067 |
| Initial CBH (cm) | 0.011 | 0.004 | 3.165 | 0.002 | 0.018 | 0.004 |
| Av. SI (Wm–2) | 0.013 | 0.001 | 8.947 | <0.002 | 0.016 | 0.01 |
| Av. VPD (Kpa) | –4.142 | 0.405 | –10.216 | <0.003 | –3.346 | –4.938 |
| (Av. VPD)2 | 0.682 | 0.079 | 8.641 | <0.004 | 0.837 | 0.527 |
| CBH = circumference at breast height; Av. = Average; SI = solar irradiance; VPD = air vapor pressure deficit | ||||||
| Table 7.2. Generalized linear mixed model covariance estimates for residual and random effects (repetitions) with first-order autoregressive structure on the daily stem increments (cm) at 130 height measured on non-fertirigated trees from a cork oak plot in Avis, Portugal, between 2017 and 2020. | ||||||
| Residual effect | Coefficient | Std. Error | Z-test | p-value | 95% Conf. Interval | |
| lower | upper | |||||
| AR1 Rho | 0.338 | 0.045 | 7.591 | <0.001 | 0.248 | 0.422 |
| AR1 Diagonal | 0.707 | 0.042 | 16.782 | <0.001 | 0.629 | 0.794 |
3.3.3 Model 3: Fertirrigation campaign – fertirrigated trees
Here, VPD was not significantly related to stem increments (p > 0.05). Cork’ age, CBH, irradiance and fertirrigation where the only variables associated with increments (Table 8). The relationship between fertirrigation and stem increments maintained the cubic shape.
| Table 8.1. Generalized linear mixed model estimates of the Independent fixed effects on the daily stem increments at 130 height measured on fertirrigated trees from a cork oak plot in Avis, Portugal, during the 2017–2020 fertirrigation campaigns. | ||||||
| model term | Coefficient | Std. Error | t-student | p-value | 95% Conf. Interval | |
| lower | upper | |||||
| Intercept | –8.512 | 0.95 | –8.964 | <0.001 | –10.376 | –6.648 |
| Cork age (year) | –0.044 | 0.006 | –6.825 | <0.001 | –0.056 | –0.031 |
| Initial CBH (cm) | 0.015 | 0.003 | 5.818 | <0.001 | 0.01 | 0.02 |
| Av. SI (Wm–2) | 0.007 | 0 | 15.612 | <0.001 | 0.006 | 0.008 |
| Av. VPD (Kpa) | 0.034 | 0.807 | 0.042 | 0.966 | –1.549 | 1.618 |
| (Av. VPD)2 | –0.187 | 0.177 | –1.058 | 0.291 | –0.534 | 0.16 |
| D. fertirrigation (mm) | 0.662 | 0.072 | 9.246 | <0.001 | 0.522 | 0.803 |
| (D. fertirrigation)2 | 0.003 | 0.015 | 0.227 | 0.821 | –0.025 | 0.032 |
| (D. fertirrigation)3 | –0.034 | 0.005 | –7.388 | <0.001 | –0.042 | –0.025 |
| CBH = circumference at breast height; Av. = Average; SI = solar irradiance; VPD = air vapor pressure deficit; D. = daily | ||||||
| Table 8.2. Generalized linear mixed model covariance estimates for residual and random effects (repetitions) with first-order autoregressive structure on the daily stem increments (cm) at 130 height measured on fertirrigated trees from a cork oak plot in Avis, Portugal. between 2017 and 2020. | ||||||
| Residual effect | Coefficient | Std. Error | Z-test | p-value | 95% Conf. Interval | |
| lower | upper | |||||
| AR1 Rho | 0.166 | 0.048 | 3.481 | <0.001 | 0.071 | 0.258 |
| AR1 Diagonal | 0.436 | 0.025 | 17.289 | <0.001 | 0.389 | 0.489 |
The quadratic form of daily fertirrigation was not significant, but the analysis of predicted stem radial increments showed a flattening point at ≈ 2 mm of daily fertirrigation (Fig. 4). Uncertainty of the tangential point varied between [1.9–3.7 mm]. Variance not explained by the model was, again, better adjusted to first-order autoregressive covariance structure. The significance of the random effect covariance of the subject “tree” was p = 0.046.
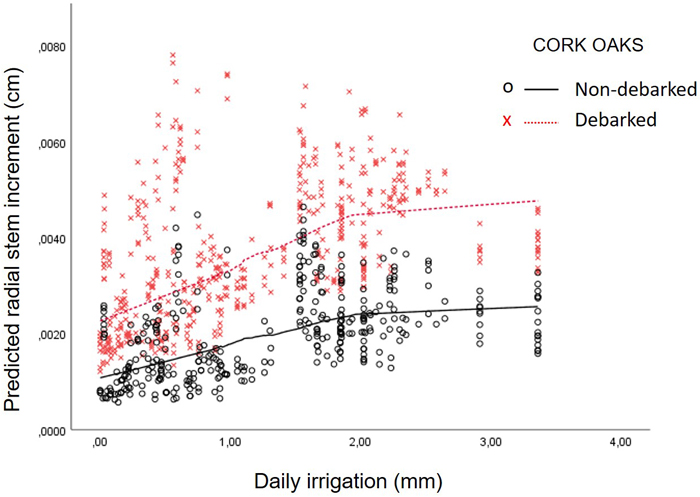
Fig. 4. Relationship between daily fertirrigation (mm) and predicted radial stem increments (cm) at a 1 ha fertirrigated cork oak plot in Avis, Portugal, calculated with the Model 3 “Fertirrigation campaign – fertirrigated trees”, separated by debarked vs non-debarked trees. Lines correspond to Kernel density using Epanechnikov function with 60% points to fit.
4 Discussion
There are several studies regarding the effect of precipitation and temperature on annual cork growth by means of dendrochronological methods due to the facility in obtaining cork samples with 9–10 years (Caritat et al. 2000; Costa et al. 2002; 2016; Paulo et al. 2021) In this study it was possible to module the effect of weather variables on much smaller periods (15–30 days) than on an annual basis (dendrochronology) which clearly facilitates the interpretation of the effect of weather variables on tree growth. Moreover, other variables such as solar irradiance and air humidity could also be analyzed. Mixed models allowed to perform time-series studies on the same subject and to infer the random effect of subject and time in the variation. The strong correlation between weather variables can make it difficult to interpret the effect of each one on growth; therefore, air temperature and humidity were combined into VPD to help reduce collinearity. Partial F statistics helped to indicate which factors are strongly linked to growth.
As expected, stem increments were associated with weather variables with a non-linear relationship, reflecting the optimal range and constraints for photosynthesis and growth. Photosynthesis is considered to be one of the most temperature-sensitive functions in the leaf (Berry and Bjorkman 1980). In this study, trees’ increment was reduced at average daily temperatures below 15 °C, and limited below 8 °C, possibly due to impairment of enzymatic processes involved in photosynthesis or, eventually freeze-thaw embolism associated with night-time freezing temperatures (Garcia-Plazaola et al. 1997; Cavender-Bares et al. 2005; Flexas et al. 2014). The sensitivity of cork oak to low temperatures may explain its well-known displacement in continental areas by deciduous trees or other, more cold-tolerant evergreens such as Quercus ilex L. (Cavender‐Bares et al. 2005). On the other hand, above 20 °C increments were still high, notwithstanding the tendency to decrease, following their great ability to acclimate to high temperatures found in Mediterranean plants (Garcia-Plazaola et al. 1997; Ghouil et al. 2003; Aranda et al. 2005).
Precipitation is a critical parameter for tree growth, reflecting water availability for the physiological processes. It is well documented the restraint in growth during long or intense drought events (Schmidt et al. 2009; Costa et al. 2016; Oliveira et al. 2016; Leite et al. 2019) and its importance for site quality estimation used in growth and vitality models (Ribeiro et al. 2003, 2006; Sánchez-González et al. 2005) and in potential aptitude (Sousa Macedo et al. 2019). However, periods of rainfall are usually non-significant or even present a negative correlation with growth from the same period (Costa et al. 2002, 2016; Paulo et al. 2021). It may be a consequence of the reduced solar irradiance and temperature during rainfall periods, therefore limiting photosynthetic rate. In fact, when analyzing precipitation with other co-variables, precipitation had a positive relationship with radial growth within its observed range in this study.
Age of the cork where dendrometers were placed also influenced stem increments, being enhanced after cork debarking and decreasing over the production cycle. This well-known pattern accounted for differences in growth over time and explained differences in growth between trees with reproduction cork and trees with their cork never debarked.
Initial CBH was also strongly associated with increment in thickness. Contrary to increments in area or perimeter – that are, respectively, exponentially and linearly related with tree’s basal area for the same radial increment – increments in radius (thickness) are not intrinsically associated with tree’s size. Therefore, the relationship between radial increments and CBH indicated that larger trees have more capacity to invest in growth. This pattern already observed (Sánchez-González et al. 2007; Paulo et al. 2017) and may be due to competing advantages. In fact, the effect of intra-competition was also detected in this study. The search index more related with competition for light (h3) presented a better association with growth than the search index measuring competition also for soil resources (d2). Trees in Irricork are under favorable soil conditions (Table 1) and nearby a water source and, therefore, may be under less pressure for soil resources. Distance to reservoir was non-significant, suggesting that their effect on groundwater may be similar across the study site. Canopy proximity caused competition for solar irradiance and affected about 40% of the trees in Irricork. On the contrary, search index d2 would consider that almost all trees would be suffering competition to a certain extent. The non-significance of competition index on the fertirrigation campaign models resulted from the uncertainty of the coefficient parameters (large SE) due to sample reduction, but the signal remained negative. It is important to mention that the negative impact of competition on radial increment does not necessarily have to be seen as an effect to be avoided. Reduction in cork thickness may be associated with improvements in cork density and quality (Poeiras et al. 2021, 2022). Cork porosity and density were already associated with stand density (Silva et al. 2017) and competition can, later on, be used to improve these cork characteristics.
4.1 Fertirrigation campaign
After the spring rains and when the summer drought takes place, fertirrigation campaigns are usually initiated, ending with autumn rains. In 2017 it last 6 months towards the extremely dry and hot weather conditions (IPMA 2017). Although 84% of the fertirrigation periods fell on days with average temperatures above 20 °C, when reduction in photosynthesis is expected to occur, fertirrigation significantly boosted increments. Increase in growth indicated that carbon assimilation was high over that period, responding directly to water availability. This increase in increments with water supply, irrespectively of VPD values, suggested that trees were able to maintain stomata open and to produce photo-assimilates even under high evaporation demands. On the other hand, trees with no fertirrigation had higher control of stomatal conductance under elevated VPD. These results are in line with the pattern observed in temperate forests (Delpierre et al. 2016), where growth halt was only triggered by VPD when soil water content was limiting. Isohydric plants such as cork oaks strongly regulate stomatal opening to avoid tissue dehydration, thus limiting carbon assimilation and growth when water potential gradient is not favorable – when water is a limiting factor and leaf-to-air VPD is elevated (Farquhar and Sharkey 1982; Faria et al. 1999; Vaz et al. 2010; Flexas et al. 2014).
Regardless of the proximity to the reservoir as well as the ability of cork trees to gather water from deep soil layers during summer drought (Otieno et al. 2006; Kurz-Besson et al. 2006; David et al. 2013; Kurz-Besson et al. 2014; Paulo et al 2015; Mendes et al. 2016), water and nutrients availability by means of fertirrigation indeed make the difference in stem increments. Growth caps at different water volumes when considering, or not, co-variables. This mismatch possibly resulted from the coincidental higher water volume supplied in 2017, when debarking occurred. The uncertainty on the upper threshold requires more research to be inferred with precision. Nevertheless, the study showed that water volume at ≈ 2 mm day–1 (140 m3 week–1) represented the upper value above which growth rate started to decline. One should highlight that this value was appropriate for the specific conditions found in the study site, namely trees’ size, soil type, soil depth, climatic profile. The cumulative effect of treatments was not yet detectable (non-significance of “treatments” factor on the full model), indicating that, to date, the concentration of fertirrigation period in late summer had no significant effect compared to a similar volume of water evenly distributed throughout the fertirrigation season. Though differential treatments for F½ and LF were initiated only in 2019.
This study was able to show that fertirrigation helped in reaching the aim of this study: time reduction until cork debarking by means of increasing trunk diameter.
This long-term study is being conducted to confirm the upper limits in the water supply that still significantly improve increments during summer drought, to analyze the best period for fertirrigation campaign according to weather conditions, as well as the cumulative effect of the treatments are still ongoing.
Both cork and wood radial growth counted for stem increments. Studies performed with the cork debarked in 2017 on Irricork showed a cork increment (rings width) larger than the observed in a rainfed plot (Poeiras et al. 2021, 2022). It is reasonable that cork repositions count for most of the observed increments on the debarked trees, as explained before. Increases in the basal area under cork can only be inferred at the end of the cork production cycle, with the next cork debarking event. The differential effect of nutrients and water cannot be tested in this study site since fertirrigation program is following the needs of the nearby olive grove fertirrigated for olive and oil production. Notwithstanding, one of the Go-Regacork project goals is to increase the economic value of agronomic irrigated marginal areas by producing dense forests for cork exploitation. Therefore, one expects that some irrigated cork oak stands will also follow fertirrigation applied for the agronomic cultures.
5 Conclusions
In conclusion, the study reinforced the overall correlation between temperature and precipitation on cork oak radial growth. The optimum daily average temperatures for growth promotion lied around 20 °C and precipitation showed a quadratic shape because of its correlation with low temperatures and irradiation. When the effect of these co-variables was considered, precipitation exerted a positive effect on radial growth.
In these young trees, larger radial size corresponded to more growth. The significance of cork’ age reflected the intense radial growth after debarking due to quicker and thicker cork layer formation, and the effect of intra-specific competition by light cone indicated competition particularly by light over other resources. Finally, the study clearly showed that water and nutrients supply through fertirrigation increased radial growth during summer drought, decoupling increments (carbon assimilation) from weather conditions, particularly VPD. When considering the effect co-variables such as weather and cork parameters, fertirrigation in a volume of ≈ 2 mm day–1 (140 m3 week–1) to trees with 50–75 CBH appeared to be the upper level above which growth rate started to slow down; the uncertainty about the cap value should be verified with further data. These results are promising in the use of fertirrigation to meet the objective of enhancing plants increments until reaching the proper size to gather profitable cork.
Availability of research materials and data
The datasets generated and analyzed during the current study are not publicly available due to confidentiality agreements between the partners.
Author contributions
Conceptualization: NAR, JMB, MV, CCA, CD. Formal analysis: CCA, NAR; Funding acquisition: NAR, CD, CCA; Investigation and data collection: CD; JAN, CCA, AP, JR, Methodology: NAR, MV, JMB, CCA, JAN; Validation: MV, JMB, NAR; Writing-original draft: CCA. Writing-review & editing, CCA, AP, JR, JAN, MV, JMB, NAR. All authors have read and agreed to the published version of the manuscript.
Acknowledgments
We are thankful to Dr. Francisco Carvalho (Amorim Florestal) and to Eng. Francisco de Almeida Garrett (H. Conqueiro) for all their support.
Funding
This work was funded by a contract-partnership between Amorim Florestal, Casa Agrícola da Herdade do Conqueiro and University of Évora; by the Rural Development Program for Operational Groups by PDR2020-101-FEADER-031427 “GO-RegaCork”, by Regacork-TraDE Project—ALT20-03-0246-FEDER-000061 and by National Funds through FCT—Foundation for Science and Technology under the Projects UID/AGR/00115/2019 and UIDB/05183/2020.
References
APCOR (2020) Anuário [yearbook] https://www.apcor.pt/portfolio-posts/boletim-estatistico-2020/. Accessed 12 December 2021.
Aranda I, Castro L, Alía R, Pardos J, Gil L (2005) Low temperature during winter elicits differential responses among populations of the Mediterranean evergreen cork oak. Tree Physiol 25: 1085–1090. https://doi.org/10.1093/treephys/25.8.1085.
Berry J, Bjorkman O (1980) Photosynthetic response and adaptation to temperature in higher plants. Annu Rev Plant Physiol 31: 491–543. https://doi.org/10.1146/annurev.pp.31.060180.002423.
Biging GS, Dobbertin M (1992) A comparison of distance-dependent competition measures for height and basal area growth of individual conifer trees. For Sci 38: 695–720. https://doi.org/10.1093/forestscience/38.3.695.
Brasier CM (1992) Oak tree mortality in Iberia. Nature 360, article id 539. https://doi.org/10.1038/360539a0.
Camilo-Alves C, Clara M, Almeida Ribeiro N (2013) Decline of Mediterranean oak trees and its association with Phytophthora cinnamomi: a review. Eur J For Res 132: 411–432. https://doi.org/10.1007/s10342-013-0688-z.
Camilo-Alves C, Dinis C, Vaz M, Barroso JM, Ribeiro NA (2020a) Irrigation of young cork oaks under field conditions-testing the best water volume. Forests 11: article id 88. https://doi.org/10.3390/f11010088.
Camilo-Alves C, Saraiva-Dias S, Dinis C, Felix MR, Varandas C (2020b) Modeling diachronic cork oak dieback–comparison of two case studies. Formath 19, article id 19.001. https://doi.org/10.15684/formath.19.001.
Caritat A, Gutiérrez E, Molinas M (2000) Influence of weather on cork-ring width. Tree Physiol 20: 893–900. https://doi.org/10.1093/treephys/20.13.893.
Cavender‐Bares J, Cortes P, Rambal S, Joffre R, Miles B, Rocheteau A (2005) Summer and winter sensitivity of leaves and xylem to minimum freezing temperatures: a comparison of co-occurring Mediterranean oaks that differ in leaf lifespan. New Phytol 168: 597–612. https://doi.org/10.1111/j.1469-8137.2005.01555.x.
Costa A, Pereira H, Oliveira A (2002) Influence of climate on the seasonality of radial growth of cork oak during a cork pro-duction cycle. Annals of For Sci 59: 429–437. https://doi.org/10.1051/forest:2002017.
Costa A, Madeira M, Santos JL (2014) Is cork oak (Quercus suber L.) woodland loss driven by eucalyptus plantation? A case study in southwestern Portugal. IForest 7: 193–203. https://doi.org/10.3832/ifor1031-007.
Costa A, Barbosa I, Roussado C, Graça J, Spiecker H (2016) Climate response of cork growth in the Mediterranean oak (Quercus suber L.) woodlands of southwestern Portugal. Dendrochronologia 38: 72–81. https://doi.org/10.1016/j.dendro.2016.03.007.
David TS, Pinto CA, Nadezhdina N, Kurz-Besson C, Henriques MO, Quilhó T, Cermak J, Chaves MM, Pereira JS, David JS (2013) Root functioning tree water use and hydraulic redistribution in Quercus suber trees: a modeling approach based on root sap flow. For Ecol Manag 307: 136–146. https://doi.org/10.1016/j.foreco.2013.07.012.
Delpierre N, Berveiller D, Granda E, Dufrêne E (2016) Wood phenology not carbon input controls the interannual variability of wood growth in a temperate oak forest. New Phytol 210: 459–470. https://doi.org/10.1111/nph.13771.
FAO and Plan Bleu (2018) State of Mediterranean forests. Food and agriculture Organization of the United Nations. Rome and Plan Bleu, Marseille. ISBN 978-92-5-131047-2. https://www.fao.org/documents/card/en/c/CA2081EN/. Accessed 10 January 2021.
Faria T, Schwanz P, PolIe A, Pereira S, Chaves MM (1999) Responses of photosynthetic and defense systems to high temperature stress in Quercus suber L. seedlings grown under elevated CO2. Plant Biol 1: 365–371. https://doi.org/10.1055/s-2007-978528.
Farquhar G, Sharkey T (1982) Stomatal conductance and photosynthesis. Annu Rev Plant Physiol 33: 317–345. https://doi.org/10.1046/j.1365-3040.2001.00660.x.
Ferreira MC, Cabral MT, Moreira T, Carvalho EC (1992) Diagnóstico das causas da anormal mortalidade dos sobeiros a sul do Tejo. [Diagnosis of the abnormal causes of cork oak’ mortality in the south of Tagus river]. Sci gerund 18, article id 205.
Flexas J, Diaz-Espejo A, Gago J, Gallé A, Galmés J, Gulías J, Medrano H (2014) Photosynthetic limitations in Mediterranean plants: a review. Environ Exp Bot 103: 12–23. https://doi.org/10.1016/j.envexpbot.2013.09.002.
Garcia-Plazaola JI, Faria T, Abadia J, Chaves MM, Pereira JS (1997) Seasonal changes in xanthophyll composition and photosynthesis of cork oak (Quercus suber L.) leaves under mediterranean climate. J Exp Bot 48: 1667–1674. https://doi.org/10.1093/jxb/48.9.1667.
Ghouil H, Montpied P, Epron D, Ksontini M, Hanchi B, Dreyer E (2003) Thermal optima of photosynthetic functions and thermostability of photochemistry in cork oak seedlings. Tree Physiol 23: 1031–1039. https://doi.org/10.1093/treephys/23.15.1031.
Hegyi F (1974) A simulation model for managing jack-pine stands. In: Fries J (ed) Growth models for tree and stand simulation. IUFRO 30: 74–90.
IPMA (2017) Boletim Climatológico Anual Portugal Continental. [Portuguese annual climate bulletin]. http://www.ipma.pt. Accessed 6 October 2021.
Kurz-Besson C, Otieno D, Lobo-Do-Vale R, Siegwolf R, Schmidt M, Herd A, Chaves M (2006) Hydraulic lift in cork oak trees in a savannah-type Mediterranean ecosystem and its contribution to the local water balance. Plant Soil 282: 361–378. https://doi.org/10.1007/s11104-006-0005-4.
Kurz-Besson C, Lobo-do-Vale R, Rodrigues ML, Almeida P, Herd A, Grant OM, Pereira JS (2014) Cork oak physiological responses to manipulated water availability in a Mediterranean woodland. Agric For Meteorol 184: 230–242. https://doi.org/10.1016/j.agrformet.2013.10.004.
Leite C, Oliveira V, Lauw A, Pereira H (2019) Cork rings suggest how to manage Quercus suber to mitigate the effects of climate changes. Agric For Meteorol 266: 12–19. https://doi.org/10.1016/j.agrformet.2018.11.032.
Macara AM (1975) Estimativa em 1975 dos prejuízos causados pelas principais doenças do sobreiro num montado da região ribatejana. [1975 Estimate of the injuries caused by the cork oaks’ main diseases at a silvopastoral system in the Ribatejo region]. Inst Prod Florestais Cortica 444: 205–212.
Mendes MP, Ribeiro L, David TS, Costa A (2016) How dependent are cork oak (Quercus suber L.) woodlands on groundwater? A case study in southwestern Portugal. For Ecol Manag 378: 122–130. https://doi.org/10.1016/j.foreco.2016.07.024.
Moreira AC, Martins JMS (2005) Influence of site factors on the impact of Phytophthora cinnamomi in cork oak stands in Portugal. For Pathol 35: 145–162. https://doi.org/10.1111/j.1439-0329.2005.00397.x.
Oliveira V, Lauw A, Pereira H (2016) Sensitivity of cork growth to drought events: insights from a 24-year chronology. Clim Change 137: 261–274. https://doi.org/10.1007/s10584-016-1680-7.
Otieno DO, Kurz-Besson C, Liu J, Schmidt MWT, Lobo-do-Vale R, David TS, Siegwolf R, Pereira JS, Tenhunen JD (2006) Seasonal variations in soil and plant water status in a Quercus suber L. stand: roots as determinants of tree productivity and survival in the Mediterranean-type ecosystem. Plant Soil 283: 119–135. https://doi.org/10.1007/s11104-004-7539-0.
Paulo JA, Palma JH, Gomes AA, Faias SP, Tomé J, Tomé M (2015) Predicting site index from climate and soil variables for cork oak (Quercus suber L.) stands in Portugal. New For 46: 293–307. https://doi.org/10.1007/s11056-014-9462-4.
Paulo JA, Pereira H, Tomé M (2017) Analysis of variables influencing tree cork caliper in two consecutive cork extractions using cork growth index modelling. Agrofor Syst 91: 221–237. https://doi.org/10.3390/f10020133.
Paulo JA, Firmino PN, Faias SP, Tomé M (2021) Quantile regression for modelling the impact of climate in cork growth quantiles in Portugal. Eur J For Res 140: 991–1004. https://doi.org/10.1007/s10342-021-01379-8.
Pinto-Correia T, Azeda C (2017) Public policies creating tensions in Montado management models: Insights from farmers’ representations. Land Use Policy 64: 76–82. https://doi.org/10.1016/j.landusepol.2017.02.029.
Pinto-Correia T, Godinho S (2013) Changing agriculture-changing landscapes: What is going on in the high valued montado landscapes of southern Portugal? Res Rural Sociol Dev 19: 75–90. https://doi.org/10.1108/S1057-1922(2013)0000019006.
Poeiras AP, Silva ME, Günther B, Vogel C, Surový P, Almeida Ribeiro N (2021) Cork influenced by a specific water regime–macro and microstructure characterization: the first approach. Wood Sci Technol 55: 1653–1672. https://doi.org/10.1007/s00226-021-01334-1.
Poeiras AP, Oliveira M, Reis J, Surovy P, Silva ME, Almeida-Ribeiro N (2022) Influence of water supply on cork increment and quality in Quercus suber L.. Cent Eur For J 68: 3–14. https://doi.org/10.2478/forj-2021-0024.
Ribeiro NA, Oliveira AC, Surový P, Pretzsch H (2003) Growth simulation and sustainability of cork oak stands. In: Amaro A, Reed D, Soares P (eds) Modelling forest systems. CABI Publishing, pp 259–267. https://doi.org/10.1079/9780851996936.0259.
Ribeiro NA, Dias SS, Surovy P, Gonçalves AC, Ferreira A, Oliveira AC (2004) The importance of crown cover on the sustainability of cork oak stands: a simulation approach. Adv Geoecol 37: 275–266. ISBN 3-923381-50-6.
Ribeiro NA, Surovy P, Oliveira AC (2006) Modeling cork oak production in Portugal. In: Hasenauer H (ed) Sustainable forest management. Growth models for Europe. Springer, pp 285–313. https://doi.org/10.1007/3-540-31304-4_18.
Ribeiro NA, Surovy P (2007) Inventário nacional de mortalidade de sobreiro na fotografia aérea digital de 2004/2006. [The Portuguese cork oak mortality inventory using 2004/2006 digital aerial photography]. ICAAM, MA-DRP, AFN, University of Evora Publishing. ISBN 978-989-8132-01-7.
Ribeiro NA, Surový P, Ferreira AG (2008) Economic implications of different cork oak forest management systems. Int J Sustain Soc 1: 149–157. https://doi.org/10.1504/IJSSOC.2008.022571.
Ribeiro NA, Surový P, Pinheiro AC (2011) Adaptive management on sustainability of cork oak woodlands. In: Manos B, Matsatsinis N, Paparrizos K, Papathanasiou J (eds) Decision support systems in agriculture food and the environment: trends applications and advances. GI Global, pp 624–636. https://doi.org/10.4018/978-1-61520-881-4.ch020.
Ribeiro NA, Surový P, Dinis C, Camilo-Alves C, Saraiva Dias S (2014) Inventário nacional de mortalidade de azinheira na fotografia aérea digital de 2004/2006. [The Portuguese holm oak mortality inventory using 2004/2006 digital aerial photography]. Sílabas e Desafios Évora. ISBN 978-989-8842-06-0.
Ritsche J, Katzensteiner K, Acácio V (2021) Tree regeneration patterns in cork oak landscapes of Southern Portugal: the importance of land cover type stand characteristics and site conditions. For Ecol Manag 486, article id 118970. https://doi.org/10.1016/j.foreco.2021.118970.
Sánchez-González M, Tomé M, Montero G (2005) Modelling height and diameter growth of dominant cork oak trees in Spain. Annals of For Sci 62: 633–643. https://doi.org/10.1051/forest:2005065.
Sánchez-González M, Calama R, Cañellas I, Montero G (2007) Variables influencing cork thickness in Spanish cork oak forests: a modelling approach. Ann For Sci 64: 301–312. https://doi.org/10.1051/forest:2007007.
Schmidt MWT, Schreiber D, Correia A, Ribeiro N, Surový P, Otieno D, Tenhunen J, Pereira JS (2009) Sap flow in cork oak trees at two contrasting sites in Portugal. Acta Hortic 846: 345–352. https://doi.org/10.17660/ActaHortic.2009.846.40.
Silva M, Marrafa S, Ribeiro N (2017) Avaliação da qualidade da cortiça em três descortiçamentos consecutivos: influência da árvore e da estrutura do povoamento. [Evaluation of cork quality between three consecutive debarking: influence of tree and stand structure]. In: Proceedings of the 8° Congresso Florestal Nacional – Raízes do Futuro, 11–14 October 2017, Viana do Castelo, Portugal. pp 179. ISBN 978-972-99656-6-1.
Sousa EMR, Santos M, Varela MC, Henriques J (2007) Perda de vigor dos montados de sobro e azinho: Análise da situação e perspectivas. [Vitality loss in cork and holm oak forests: Analysis of the situation and perspectives]. https://www.iniav.pt/images/publicacoes/livros-manuais/montados_sobro_azinho_analise.pdf. Accessed 8 November 2013.
Sousa Macedo A, Alves A, Igreja A, Pinto-Gomes C, Alexandre C, Luís C, Viliotis C, Malha F, Costa Lima F, Paulo Fonseca J, Barroqueiro M, Raposo M, Aires N, Oliveira N, Ribeiro N, Crespo R, Saraiva Dias S, Morais S (2019) Programa Regional de Ordenamento Florestal Alentejo, Capítulo B – Caracterização biofísica socioeconómica e dos recursos florestais. [Forest Management Regional Program for Alentejo, Chapter B – Biophysical socioeconomic and forest resources characterization]. ICNF, Lisboa.
Vaz M, Pereira JS, Gazarini LC, David TS, David JS, Rodrigues A, Maroco J, Chaves MM (2010) Drought-induced photosynthetic inhibition and autumn recovery in two Mediterranean oak species (Quercus ilex and Quercus suber). Tree Physiol 30: 946–956. https://doi.org/10.1093/treephys/tpq044.
Total of 54 references.

