How to implement the data collection of leaf area index by means of citizen science and forest gamification?
Zhang S., Korhonen L., Nummenmaa T., Bianchi S., Maltamo M. (2024). How to implement the data collection of leaf area index by means of citizen science and forest gamification? Silva Fennica vol. 58 no. 5 article id 24044. https://doi.org/10.14214/sf.24044
Highlights
- Citizen science and gamification are proposed for collecting in situ forest leaf area index data
- LAI can be estimated by taking smartphone images of forest canopies at 57° zenith angle
- Twenty smartphone images per plot are enough to obtain accurate LAI measurements
- Additional images may be required in forests with dense or uneven canopy structure.
Abstract
Leaf area index (LAI) is a critical parameter that influences many biophysical processes within forest ecosystems. Collecting in situ LAI measurements by forest canopy hemispherical photography is however costly and laborious. As a result, there is a lack of LAI data for calibration of forest ecosystem models. Citizen science has previously been tested as a solution to obtain LAI measurements from large areas, but simply asking citizen scientists to collect forest canopy images does not stimulate enough interest. As a response, this study investigates how gamified citizen science projects could be implemented with a less laborious data collection scheme. Citizen scientists usually have only mobile phones available for LAI image collection instead of cameras suitable for taking hemispherical canopy images. Our simulation results suggest that twenty directional canopy images per plot can provide LAI estimates that have an accuracy comparable to conventional hemispherical photography with twelve images per plot. To achieve this result, the mobile phone images must be taken at the 57° hinge angle, with four images taken at 90° azimuth intervals at five spread-out locations. However, more images may be needed in forests with large LAI or uneven canopy structure to avoid large errors. Based on these findings, we propose a gamified solution that could guide citizen scientists to collect canopy images according to the proposed scheme.
Keywords
forest canopy;
crowdsourcing;
hinge angle;
plant area index;
smartphones
-
Zhang,
School of Forest Sciences, University of Eastern Finland, Yliopistokatu 7, FI-80101 Joensuu, Finland
 https://orcid.org/0000-0001-7876-9635
E-mail
shaohui.zhang@uef.fi
https://orcid.org/0000-0001-7876-9635
E-mail
shaohui.zhang@uef.fi

-
Korhonen,
School of Forest Sciences, University of Eastern Finland, Yliopistokatu 7, FI-80101 Joensuu, Finland
 https://orcid.org/0000-0002-9352-0114
E-mail
lauri.korhonen@uef.fi
https://orcid.org/0000-0002-9352-0114
E-mail
lauri.korhonen@uef.fi
-
Nummenmaa,
Tampere University, Kalevantie 4, FI-33100 Tampere, Finland
 https://orcid.org/0000-0002-9896-0338
E-mail
timo.nummenmaa@tuni.fi
https://orcid.org/0000-0002-9896-0338
E-mail
timo.nummenmaa@tuni.fi
-
Bianchi,
Natural Resources Institute Finland (Luke), Latokartanonkaari 9, FI-00790 Helsinki, Finland
 https://orcid.org/0000-0001-9544-7400
E-mail
simone.bianchi@luke.fi
https://orcid.org/0000-0001-9544-7400
E-mail
simone.bianchi@luke.fi
-
Maltamo,
School of Forest Sciences, University of Eastern Finland, Yliopistokatu 7, FI-80101 Joensuu, Finland
 https://orcid.org/0000-0002-9904-3371
E-mail
matti.maltamo@uef.fi
https://orcid.org/0000-0002-9904-3371
E-mail
matti.maltamo@uef.fi
Received 7 August 2024 Accepted 18 November 2024 Published 28 November 2024
Views 34507
Available at https://doi.org/10.14214/sf.24044 | Download PDF

Supplementary Files
1 Introduction
Leaf area index (LAI), here defined as half of the two-sided leaf area per unit ground surface, is a fundamental parameter that provides insights into understanding ecosystem dynamics and functioning (Chen and Black 1992). It quantifies the extent of foliage within a vegetative canopy and has been included as one of the most crucial variables of many global biosphere-atmosphere models (GCOS 2022). For example, LAI plays an essential role in understanding primary productivity, transpiration and other bio-physical processes related to the complex interplay between vegetation and atmosphere (Ryu et al. 2011). It is also a key input in land surface and climate models that require continuous and consistent LAI over large areas (Yuan et al 2011). In forest ecosystems, LAI contributes to biodiversity assessment (Skidmore et al. 2015) and serves as an indicator of forest health (Hanssen and Solberg 2007).
Despite of its importance, LAI has remained as an underrepresented forest attribute in forest inventories that emphasise commercially important forest attributes such as tree height, mean diameter and growing stock volume. Collecting LAI data in the field requires specific skills and equipment, which may have attributed to its negligence. The majority of LAI data measured in the field are obtained using indirect measurements such as digital hemispherical photographs (DHPs) and digital canopy photographs (DCPs). Previous research has obtained accurate LAI estimates at plot level using 12 DHPs or 32 DCPs (Macfarlane et al. 2007; Zhang et al. 2024); therefore, it is labour intensive and time consuming to collect LAI data over large geographical areas. In addition, taking DHP images requires proper assessments of weather conditions prior to taking the images (Díaz et al. 2021; Kaha et al. 2023). Failure to do so leads to a considerable degradation in data quality. Thus, there is a need to collect large quantities of LAI data over broad geographical extents to understand complex forest challenges stemming from both natural and anthropogenic sources. Meanwhile, novel approaches to data collection are needed to decrease the complexity and cost of field data acquisitions.
Thanks to the recent advancement in information technology, citizen science (CS) has expanded extensively as a new research approach (Kobori et al. 2016). It has gained momentum in engaging both researchers and volunteers alike to collect data and explore scientific research topics in various fields (Silvertown 2009). Participatory CS research has also been successfully implemented in many forest contexts. For example, CS projects have showcased their contribution to monitoring forest pests and pathogens (de Groot et al. 2022) and mapping forest decline (Crocker et al. 2023). In addition, data collected from CS projects has been proven useful in validating products of land surface phenology obtained from remote sensing data (Purdy et al. 2023). One important advantage of CS projects lies in the capacity of mobilising citizen scientists to collect large quantities of data on scales that would be challenging for researchers alone to obtain. This provides a potential solution to tackle the lack of large-area LAI data collected in the field. Although CS utilises collective efforts to address data shortage issues, data quality is reportedly a potential challenge especially when citizen scientists deemed their activities as not “interesting” (Dickinson et al. 2010). To mitigate this issue, incorporating forest gamification into CS has emerged as a promising solution, if the game provides sufficient incentives for the participants.
Forest gamification is defined as designing game contents within the context of forest ecosystems. An integral aspect of gamification involves crafting game-like frameworks that provide guidance for individuals to follow and complete tasks. The goal of gamification is often to encourage people to willingly participate in activities that might otherwise be considered as dull or mundane. By establishing specific rules and requirements prior to tasks, gamified CS projects can encourage participants to collect data in an enjoyable and engaging manner. Positive results have been shown in many contexts about how forest gamification has transformed the way common citizens perceive, understand and protect forest ecosystems (Vastaranta et al. 2022). Another recent example was the gamified forest laser scanning project where participants collected point cloud data while engaging in multiple playful activities (Nummenmaa et al. 2024).
This gamified approach presents a potential solution to mitigate the risk of lacklustre spirits of the participants, a commonly seen factor that leads to diminished data quality in CS projects. Mobile devices have been widely used to enhance the gaming experience, as most of them nowadays are enhanced with a wide range of different sensors, such as cameras, inertia sensors and positioning systems. This also provides a great opportunity for citizen scientists to take directional photography and facilitate LAI data collection.
When using indirect optical measurements, LAI can be derived from other forest canopy variables such as gap fractions according to the Beer-Lambert law. Previous studies have employed this approach to estimate leaf area index, for example by using inclined smartphone cameras (Qu et al. 2021). Furthermore, smartphone applications like LAISmart (Qu et al. 2017) and PocketLAI (Confalonieri et al. 2013) have been developed to estimate LAI. Given the impracticality of expecting citizen scientists to possess cameras with fisheye lenses, directional photography with smartphone cameras seems more suitable and realistic. Directional canopy photography is mainly taken at zenith (DCPs) or the so-called ‘hinge angle’, i.e. 57° from zenith, which has several advantages (Yan et al. 2019). For example, it is less sensitive to camera exposure and can be applied in all light conditions. The inbuilt sensor technology of smartphones can make it easy for citizen scientists to take forest canopy images at the hinge angle in a gamified way. Subsequently, LAI can be calculated from the images, assuming that the gap fraction interpreted from the images is representative. This requires that the hinge angle is correctly estimated, the gap fraction is estimated reliably, and there are enough samples per stand.
The inspiration of this study drew insights from our previous real-world experiences with a CS programme called Metsänvalo (https://uniteflagship.fi/metsanvalo). The data collection was planned based on an existing protocol (Arietta 2022). It required participants to collect Google Street View spherical panoramas (Google LLC) that could be converted to DHPs. We recognised that the implementation of CS has its own challenges. Recruiting and retaining citizen scientists was particularly difficult, as many of them found the tasks laborious and then their interest quickly disappeared. In addition, the data quality was poor without proper supervision due to the complexity of the spherical picture collection. Recognising these challenges, we propose an integration of CS and forest gamification as a potential solution to make data collection easier and more reliable. In real-world conditions, it is difficult to keep the smartphone fixed at designed angle, as the camera is hand-held by an operator without fixed support. The utilisation of built-in smartphone sensors within the gamification framework can help to fix the inclination angle at 57°.
The main objective of this study is to determine how citizen scientists should be guided to obtain satisfactory LAI estimates by taking forest canopy images with consumer-grade smartphone cameras. We present an empirical simulation study that aimed at determining how many smartphone images and image locations are needed to replicate accurate LAI data collection, which is typically done by taking twelve DHPs per sample plot (Majasalmi et al. 2012). We also discuss gamification options that could make canopy image collection fun and engaging for citizen scientists and propose how a practical data collection experiment could be organized in the future.
2 Materials and methods
2.1 LAI calculations
The theoretical basis of calculating LAI using camera-based indirect measurement is the Beer-Lambert’s extinction law. It was originally used to describe the empirical relationship of light attenuation when passing through a uniform medium and later applied to describe light interception of homogeneous forest canopies (de Wit 1965). LAI can be derived using canopy gap fraction at specific angles following Eq. 1:
![]()
where θ is the viewing angle from zenith, T is the gap fraction and G(θ) is the foliage projection function.
When gap fractions are measured at a series of discrete zenith angles, the above equation can be estimated using to Miller’s integral (Miller 1967) as Eq. 2:

The calculation of LAI according to this formula thus requires no prior knowledge on angular gap fractions covering the entire hemisphere (Miller 1967). In this way, the G function can be omitted.
Another less common way of calculating LAI is using the gap fraction at the so-called “hinge angle” (57° from zenith) because the leaf projection G function remains constant (0.5) at this angle (Wilson 1963) as Eq. 3:
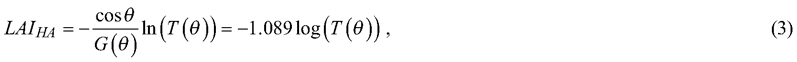
when θ = 57°, cos θ ≈ 0.5446 and G(θ) = 0.5 (Wilson 1963), thus the coefficient –1.089 (Zhao et al. 2019).
2.2 Study sites
The data were collected from 126 plots across three study sites in southern Finland. Table 1 shows their forest attributes i.e., LAI, dominant height and basal area, measured in the field. The main tree species included Scots pine (Pinus sylvestris L.), Norway spruce (Picea abies (L.) H. Karst.) and birches (Betula spp. L.). The plots were placed subjectively to cover a wide diversity of forest structures, ranging from sparsely stocked pine bogs to mixed old growth and extremely dense young forests. The large range of LAI values made it suitable for our simulation study.
| Table 1. Forest attributes at plot level across the three study sites in Finland. | ||||
| Site | Suonenjoki | Hyytiälä | Liperi | |
| n | 20 | 86 | 20 | |
| Coordinates of the centres | 62°40´N, 27°07´E | 61°50´N, 24°17´E | 62°29´N, 29°05´E | |
| LAI | min. | 0.10 | 0.25 | 0.15 |
| mean | 1.99 | 2.23 | 2.04 | |
| max. | 3.71 | 4.17 | 4.19 | |
| sd | 0.90 | 0.85 | 1.04 | |
| Dominant height (m) | min. | 4.0 | 2.2 | 4.2 |
| mean | 15.7 | 16.8 | 16.2 | |
| max. | 26.9 | 34.3 | 32.6 | |
| sd | 6.5 | 6.8 | 7.0 | |
| Basal area (m2 ha–1) | min. | 4.0 | 0.5 | 1.0 |
| mean | 18.1 | 23.1 | 18.1 | |
| max. | 34.0 | 51.3 | 44.0 | |
| sd | 8.3 | 10.6 | 11.2 | |
| Abbreviations: LAI (leaf area index), min (minimum), max (maximum), sd (standard deviation). | ||||
2.3 Digital hemispherical photographs as reference data
DHP data from the three sites were collected in different years: Hyytiälä, Suonenjoki, and Liperi in 2011, 2015 and 2016 respectively. The images were acquired using a Nikon Coolpix 8800 camera and an FC-E9 fisheye converter under overcast or near sunset to avoid the impact of direct sunlight on image quality. Twelve DHPs were taken at each plot following the measurement scheme displayed in Fig. 1. During the measurement, the camera was fixed to a tripod at approximately 1.3 m height above ground. The camera was then levelled using a two-axis bubble level. Next, the lens was adjusted to face upwards with its focus set to infinity. Exposure was adjusted prior to taking the images at each plot so that contrast between the sky and the canopy was optimized. The shooting mode was set to aperture priority with aperture kept at f/2.8–f/4.5 depending on illumination. The DHPs were saved in raw image format.
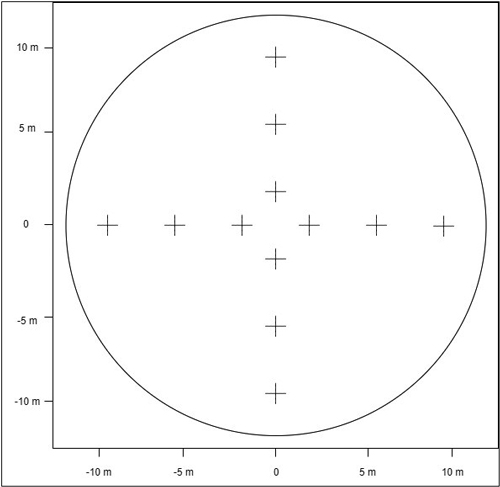
Fig. 1. Twelve measurement locations where digital hemispherical photographs (DHPs) were taken to estimate leaf area index within each r = 12.5 m plot.
The DHPs were processed using the software Hemispherical Project Manager (HSP) that implements the LinearRatio method (Cescatti 2007) for a single camera (Lang et al. 2017). The software first converts the raw DHPs to 16-bit simple portable grey maps (PGM format) with the help of dcraw software (version 9.28) (Coffin 2014). Only original blue pixels were extracted in the process because at this spectrum they have the highest contrast between the sky and the canopy. We used the switches of dcraw: -d (document mode, no colour and interpretation), -W (do not automatically brighten the image), -g 1 1 (linear 16-bit custom gamma curve). The final output was binarized hemispherical images, where gap fractions T(θ) were derived following the ring-wise analysis.
Specifically, DHPs were divided into 5 concentric rings with 15° interval (0–75°). The weights of each ring were calculated as Eq. 4:

where θi was the mean zenith angle of the ring (7°, 23°, 38°, 53°, and 68°), and Wi represents the weighting factor that is proportional to sin(θ) dθ in Eq. 2 and normalised to sum to 1. Note that the weight of the missing the 6th ring was assigned to the 5th ring, similar to the LAI-2000 plant canopy analyser instrument (Welles and Norman 1991).
As measurements were only available at the 5 rings, the final LAI from Eq. 2 can be weighed as Eq. 5:

where ![]() are the mean gap fractions from the DHPs collected at plot level for each annulus ring. Note that the effect of woody components (such as tree trunks and branches) was not removed here, because clumping corrections are not within our interest in this study; therefore, LAI in practice denotes plant area index (PAI).
are the mean gap fractions from the DHPs collected at plot level for each annulus ring. Note that the effect of woody components (such as tree trunks and branches) was not removed here, because clumping corrections are not within our interest in this study; therefore, LAI in practice denotes plant area index (PAI).
2.4 Simulation scenarios and processes
Data collection in the forest can be implemented in many different ways. The optimal data collection scheme is a trade-off between the required accuracy and the complexity of acquisition. Here, the question under investigation was simplified to the selection of number of locations where photographs are taken within a single plot, as well as the number of photographs to be taken from each location. The simulation was based on sub-sampling the available hemispherical image data. Thus, there were twelve potential locations where images could be simulated. Table 2 detailed the scenarios tested in this study, with each scenario characterised by varying numbers of images to be taken at different observation spots.
| Table 2. Simulation scenarios of the number of digital hemispherical photographs to estimate leaf area index. | ||||||||||||||||||
| Scenario ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| No. location | 1 | 1 | 1 | 1 | 2 | 4 | 2 | 4 | 5 | 10 | 6 | 3 | 7 | 8 | 4 | 6 | 9 | 5 |
| No. images per location | 1 | 2 | 3 | 4* | 2 | 1 | 4* | 2 | 2 | 1 | 2 | 4* | 2 | 2 | 4* | 3 | 2 | 4* |
| Total No. images | 1 | 2 | 3 | 4 | 4 | 4 | 8 | 8 | 10 | 10 | 12 | 12 | 14 | 16 | 16 | 18 | 18 | 20 |
| Scenario details featured different locations where canopy images were simulated per location. Thus, the total number of images (Total No. images) equals the number of locations (No. location) multiplied by the number of images per location (No. images per location). * With four images simulated at 90° azimuth intervals per location. | ||||||||||||||||||
The simulation process started by random sampling of the centre coordinates (φ, θ) of the simulated mobile phone image. The azimuth angle was simulated randomly within the range of 0to 360°, as in a forest gamification setting, citizen scientists could freely capture canopy images at various azimuthal angles. The zenith angle remained constant (57°) as it is crucial to derive LAI at this angle without having to consider the whole hemisphere. As modern smartphone cameras often have a horizontal viewing angle of about 60° and a vertical viewing angle of about 50°, the simulated image sizes should align with these specifications for accuracy. Therefore, the maximum and minimum horizontal viewing angles of the simulated images were set to φ ± 30°. Our preliminary tests revealed that altering the ring width i.e., zenith angle range, did not significantly affect the gap fractions obtained from simulated images, unless it exceeded 15°. Thus, the vertical scope of the simulated image was confined within the range of ±7.5° from the hinge angle (i.e., 49.5°–64.5°). This angle-defined boundary box was used to extract gap fractions from the real DHP images captured in the field, and consequently calculate the LAI (Fig. 2). Assuming the gap fraction T(θ) from the masked region was equivalent to that of the whole hinge angle, the simulated LAI at the hinge angle (LAIHA) was calculated following Eq. 3.

Fig. 2. Hemispherical photograph with the dash line marks the hinge angle (θ = 57°) and the mask covered 60° azimuth and ± 7.5° around the hinge angle was used to simulate smartphone canopy images.
2.5 Accuracy assessment
The gap fraction T(θ) of each simulated image was extracted from DHP images. Depending on the scenarios, the LAIHA was calculated by taking the average of the logarithms of individually simulated T(θ) (Ryu et al. 2010). Take Scenario 18 for instance, where four images were simulated from five different locations. Thus, a total of 20 images were simulated, and the T(θ) at simulation level was then obtained as the average of the 20 simulated gap fraction samples. Next, gap fraction at simulation level was used as the input of Eq. 3 and subsequently LAIHA was calculated for each simulation. For each plot, this was reiterated 100 times. The simulation accuracy at plot level was assessed using RMSE% (Eq. 6) and the standard deviation (SD, Eq. 7) of simulated LAIHA:


where LAI was measured by DHPs at plot level, LAIHA was obtained from simulated images using truncated gap fraction per simulation, ![]() denoted the mean of LAIHA and n was the number of simulations per scenario (100).
denoted the mean of LAIHA and n was the number of simulations per scenario (100).
The performance of each scenario was assessed using the mean RMSE% (![]() , Eq. 8) and mean SD (
, Eq. 8) and mean SD (![]() , Eq. 9) of all plots. To better illustrate, the field measured LAIs were stratified into four categories based on their quartiles, namely: Q1 (0–25%), Q2 (25–50%), Q3 (50–75%) and Q4 (75–100%).
, Eq. 9) of all plots. To better illustrate, the field measured LAIs were stratified into four categories based on their quartiles, namely: Q1 (0–25%), Q2 (25–50%), Q3 (50–75%) and Q4 (75–100%).


where RMSE% and SD were obtained for each simulation at plot level and m was the number of plot (127).
Furthermore, we linked the performance of the best scenario with the measured forest attributes to determine if the accuracy of estimation was dependent on the forest structure. Specifically, we regressed the mean absolute residual ![]() (Eq. 10) and its normalised value
(Eq. 10) and its normalised value ![]() (Eq. 11) of each plot against field-measured forest attributes. Absolute values were used because we wanted to give both under- and overestimations equal weights. The amount of error is different depending on whether the error is a percentage or not, so both cases were analysed. Field-measured forest attributes as independent variables included basal area (BA), diameter (DBH), height (H) and crown base height (CH) of the basal area median tree measured using a relascope.
(Eq. 11) of each plot against field-measured forest attributes. Absolute values were used because we wanted to give both under- and overestimations equal weights. The amount of error is different depending on whether the error is a percentage or not, so both cases were analysed. Field-measured forest attributes as independent variables included basal area (BA), diameter (DBH), height (H) and crown base height (CH) of the basal area median tree measured using a relascope.


3 Results
3.1 Comparison of simulation scenarios
At scenario level, the accuracy improved together with the number of simulated images used to obtain plot-level T(θ) and LAIHA (Fig. 3). Scenario 1 (one image at one random location and azimuth angle) produced the lowest accuracy, with ![]() and
and ![]() reaching 51.9% and 0.886 respectively. The best accuracy was achieved by Scenario 18 (twenty images in total, with four images simulated at 90° azimuth intervals from five different locations), yielding the
reaching 51.9% and 0.886 respectively. The best accuracy was achieved by Scenario 18 (twenty images in total, with four images simulated at 90° azimuth intervals from five different locations), yielding the ![]() of 10.2% and
of 10.2% and ![]() of 0.170.
of 0.170.
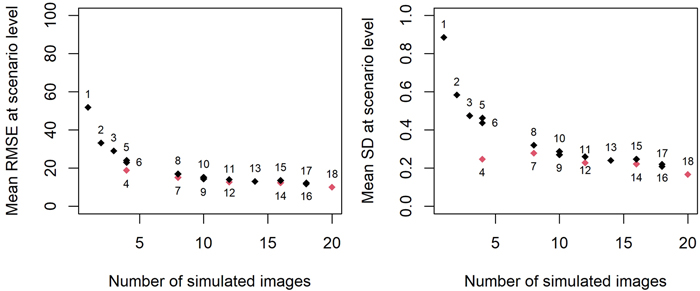
Fig. 3. Non-linear relationship between the numbers of simulated smartphone canopy images and their ![]() (left) and
(left) and ![]() (right) at scenario level. The labels represented Scenario IDs and red colour denoted scenarios where images were simulated at 90° azimuth intervals. Scenario 18 was selected for further inspection.
(right) at scenario level. The labels represented Scenario IDs and red colour denoted scenarios where images were simulated at 90° azimuth intervals. Scenario 18 was selected for further inspection.
We observed a slight improvement in accuracy when using the technique of simulating images at 90° azimuth intervals (red in Fig. 3), compared to simulating images at random azimuth angels (black in Fig. 3). For example, Scenario 4 achieved a gain in accuracy (![]() on average 4.3 % less) compared to Scenarios 5 and 6, where the four images were taken in random directions instead of using 90° intervals. This benefit was also noticeable in Scenarios 7, 12 and 14. In contrast, Scenarios 8, 11 and 15, which used the same number of simulated images but did not employ the 90° azimuth interval technique, showed slightly lower accuracies. In addition, we did not observe a significant impact of the randomly selected locations on accuracy.
on average 4.3 % less) compared to Scenarios 5 and 6, where the four images were taken in random directions instead of using 90° intervals. This benefit was also noticeable in Scenarios 7, 12 and 14. In contrast, Scenarios 8, 11 and 15, which used the same number of simulated images but did not employ the 90° azimuth interval technique, showed slightly lower accuracies. In addition, we did not observe a significant impact of the randomly selected locations on accuracy.
A non-linear relationship between the number of simulated images and accuracy was observed (Fig. 3), due to the logarithmic nature of LAI computation (Eq. 5). The reference LAI was derived from a set of 12 DHPs taken at different locations within the plot, each covering 360° azimuth angles. In contrast, the simulated images had a narrower horizontal 60° view, which is similar to commonly used commercial smartphone cameras. Therefore, it would take approximately 12 × 360/60 ≈ 72 images without overlap to achieve equivalent coverage across the azimuthal area.
In theory, we could continue to simulate more images; however, considering practicality and feasibility, it was necessary to propose an optimal research design to guide a gamified CS project. Therefore, we had to determine the optimal number of images and their locations required to achieve optimal LAI estimation that closely approximates observed counterparts in the field. It seemed that the trend of ![]() at scenario level transited to a smoother decline after simulating four images, after which the decline became less prominent with additional simulated images. Scenario 4 (Four images, at 90° azimuth intervals at one location) also yielded satisfactory results. Nevertheless, as Scenario 18 yielded the best accuracy among all the proposed scenarios so far, we selected it for further investigation.
at scenario level transited to a smoother decline after simulating four images, after which the decline became less prominent with additional simulated images. Scenario 4 (Four images, at 90° azimuth intervals at one location) also yielded satisfactory results. Nevertheless, as Scenario 18 yielded the best accuracy among all the proposed scenarios so far, we selected it for further investigation.
3.2 Plot level inspection by LAI categories with Scenario 18
At plot level, we inspected the simulated LAIHA obtained from Scenario 18 using 100 repetitions and compared the result with LAI values observed in the field. The observed LAI values were divided into four quantiles (Q1–Q4) and the results were analysed by group.
In the Q1 group (LAI: 0.10 to 1.46, 31 plots, Fig. 4a), the simulated LAIHA values closely aligned with observed LAI at plot level. In 20 of the 31 plots, the observed LAI fell within the interquartile range (IQR, i.e., inside the box) of simulated LAIHA, and in ten plots, within the upper whisker. RMSE% ranged from 3.8% to 37.7% and SD from 0.030 to 0.167. The highest RMSE% was observed at Plot 98 (SD = 0.031), while Plot 77 had the highest SD (RMSE% = 0.117), indicating that the highest RMSE% did not necessarily correspond to the highest SD.
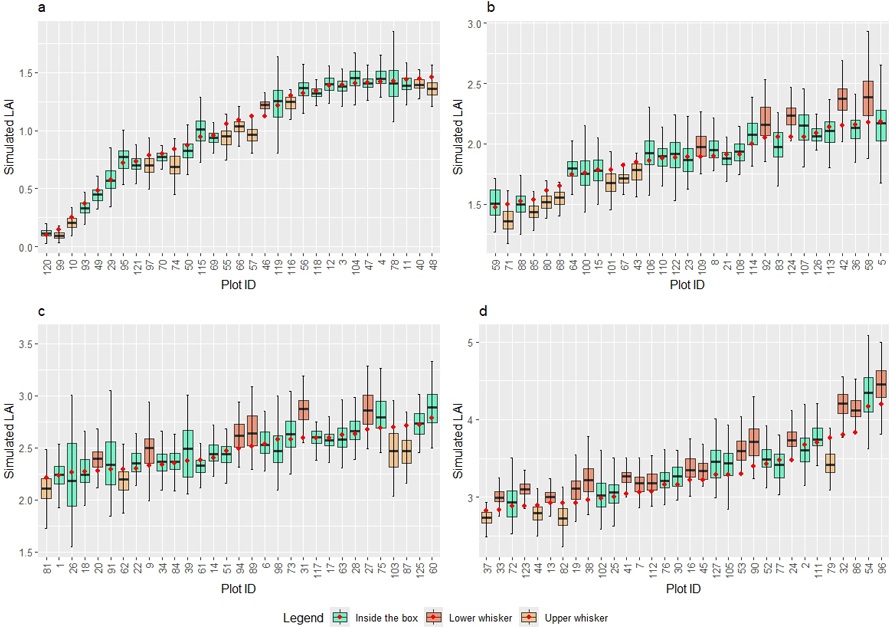
Fig. 4. Boxplots illustrating the simulated leaf area index and their observed counterparts (red dot) at plots based on their leaf area index quantiles: Q1 (a), Q2 (b), Q3 (b) and Q4 (d). View larger in new window/tab.
In the Q2 group (LAI: 1.47 to 2.18, 31 plots, Fig. 4b), the simulated LAIHA values generally matched with the observed LAI values. Nineteen plots had observed LAI within the IQR, while five were within the lower whisker and seven within the upper whisker. RMSE% ranged from 3.1% to 21.5% and SD from 0.057 to 0.215.
In the Q3 group (LAI: 2.21 to 2.78, 31 plots, Fig. 4c), the results were similar. The simulated LAIHA values remained close to their observed counterparts, with 21 plots having observed LAI within the IQR of the simulated LAIHA. Six plots were within the lower whisker and four within the upper whisker. The RMSE% ranged from 3.3% to 16.5% and SD from 0.081 to 0.375.
In the Q4 group (LAI: 2. 83 to 4.19, 32 plots, Fig. 4d), only twelve plots had their observed LAI values falling within the simulated IQR. Sixteen plots were within the lower whisker and four within the upper whisker. The RMSE% ranged from 4.5% and 11.7% and SD from 0.100 to 0.349.
To sum up, following the settings of Scenario 18, the simulated LAI approximated the observed LAI across almost all plots. The RMSE% across all plots was within the bounds between 3.1% and 37.7% and the SD was between 0.031 and 0.375. At plots where LAI was small (such as the first and second quartiles), the simulated LAIHA values tended to underestimate the observed LAI. Following a thorough examination, this often happened at seedling plots, where big seed trees exerted a substantial impact on estimated gap fractions (Fig. 5a). The disruption in canopy gap continuity therefore resulted in significant underestimation of simulated gap fractions if simulation was based on these azimuth angles, which subsequently led to an overestimation of simulated LAIHA. The opposite was observed at plots with larger LAI (such as the fourth quartile), where the simulated LAIHA was more likely to overestimate its observed counterpart. In plots characterised by dense forest canopy cover, the simulation was sensitive to irregular large canopy gaps occurring at random azimuth angles (Fig. 5b). When the simulation with 90° azimuth intervals failed to adequately capture these areas, the simulated gap fractions became underestimates, and consequently yielded an overestimation of LAIHA.

Fig. 5. Binary digital hemispherical photographs where gap fraction was influenced by seed trees in seedling stand (a) and by small random big gaps on a dense canopy stand (b).
Finally, we built linear regressions using the non-normalized and normalised mean absolute residual ![]() with basal area (BA) and diameter of the basal area median tree (DBH) as independent variables. The final models were:
with basal area (BA) and diameter of the basal area median tree (DBH) as independent variables. The final models were:
![]()
![]()
BA and DBH were statistically significant in both models at p < 0.005. The models did not include either H or CH, as H was strongly correlated with DBH (correlation 95%), and CH was not statistically significant as a predictor. Overall, the model residuals scattered around zero (Fig. 6).
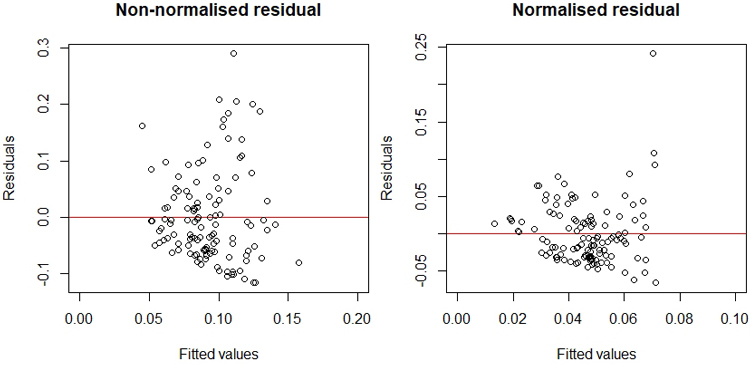
Fig. 6. Residual analysis with the scatter plots of the non-normalised mean absolute model residuals ![]() (left) and the normalised mean absolute model residuals
(left) and the normalised mean absolute model residuals ![]() (right) with fitted values.
(right) with fitted values.
4 Discussion
4.1 Estimating LAI using truncated gap fraction from canopy images
The fundamental basis for estimating LAI used in this study is to first infer the full gap fraction at hinge angle using a sampled partial gap fraction, as the G function at this angle remains constant at 0.5. Our study followed the same approach to estimate LAI using simulated and truncated canopy images obtained from full hemispherical images. In the simulation design, the searching region was restricted to the viewing angles of 50° vertically and 60° horizontally to mimic the configuration of consumer-grade smartphone cameras. However, only a narrow strip of 15° at vertical angles was extracted around the hinge angle (± 7.5°), as the ring width would greatly affect the simulation results. On one hand, the canopy gap information may not be well extracted if the ring width is too narrow. On the other hand, the assumption on the G function could be violated if the ring width is too wide, which would result in biased estimation. Previous literature used the hinge region of 55–60° zenith (± 2.5°) to extract canopy gap fraction and subsequently retrieve LAI (Calders et al. 2018). In our simulation, we used a wider region to sample gap fraction, as our preliminary test discerned that the alteration in ring width did not exert significant impacts on the sampled gap fractions at the hinge angle, unless the total ring width surpassed the threshold of 15°. We also decided to adopt the searching region with the ring width of 15° to keep it consistent with the ring divisions of DHP images. Following this design, the results overall yielded good performance.
In this study, no adjustments were applied to correct for the presence of woody elements and the leaf clumping, which would be needed for the estimation of true LAI. Obtaining clumping corrections for hinge angle photographs could however be obtained from the gap size distribution method that has previously been applied with hemispherical images (Chen and Cihlar 1995), as it is possible to distinguish small and large gaps using e.g. morphological image analysis (Korhonen and Heikkinen 2009). Correction for woody canopy elements at the hinge angle remains as a challenge, but for example deep learning approaches could be used for this purpose (Moorthy et al. 2019). In practice, we however noted that that the woody canopy elements at the hinge angle were frequently obscured by leaf material compared to larger zenith angles closer to horizon, so we can assume that this effect is relatively small. Finally, the plant area index that we obtained from the images is an important ecological variable on its own, and governs key canopy processes such as light absorption and precipitation interception.
As this study implemented simulations based on DHPs collected in flat terrains, the slope effect on LAI estimation was not considered. Although the slope effect is relatively small and negligible when the slope is less than 30° (Yan et al. 2019), it is still important to highlight the necessity of considering the slope effect in the context of providing guidance to gamification and CS programmes. Given that citizen scientists may not be well trained to collect research data, we suggest that they should be instructed not to take forest canopy images on slopes to minimise or avoid such impact.
4.2 Implications on forest gamification and CS design
Through simulation, this study tested and proved the feasibility of obtaining relatively reliable LAI estimates via forest gamification and CS programmes. The main objective of the study was to instruct how many and at which locations should forest canopy images be taken when citizen scientists collect field data. The simulation results at scenario level (Scenario 18) indicated that a total number of 20 forest canopy images taken at the hinge angle was sufficient to obtain relatively accurate LAI estimates ![]() (10.2%). Although the location at which the images are taken did not exert a significant influence on the results, it is still recommended that the locations should vary and spread out to reduce the likelihood of repetition. In addition, it appeared that taking canopy images at 90° azimuth intervals at multiple locations could further improve the estimation accuracy.
(10.2%). Although the location at which the images are taken did not exert a significant influence on the results, it is still recommended that the locations should vary and spread out to reduce the likelihood of repetition. In addition, it appeared that taking canopy images at 90° azimuth intervals at multiple locations could further improve the estimation accuracy.
Image acquisition and analysis has been employed in many previous CS projects due to the ubiquity of mobile devices. A thorough review on the CS projects related to natural environments in the UK reported that approximately one third required photographs (Roy et al. 2012). More specific image-based CS projects have, for example, assessed their performance in improving forest health in the U.S (Crocker et al. 2020) as well as in monitoring plant species diversity in urban environments in China (Yang et al. 2021).
Notably, many existing CS projects only require participants to take one photograph at a time to complete their assigned data collection tasks. Our simulation results showed that such approach does not provide reliable enough LAI estimates (Scenario 1). Based on our previous CS project experience, simply asking citizen scientists to venture in forest and collect images according to scientists’ plans did not produce expected outcomes, which was mainly due to the lack of interest and stimulation as well as the lack of proper guidance. Thus, the requirement of 20 images in total may be regarded laborious or even arduous by participants and consequently dismay their level of commitments. This concern also led us to stop simulating scenarios with more images due to already-high computational costs. Alternatively, Scenario 4 – taking 4 images with 90° azimuth intervals at one location – yielded adequate results.
The analysis of mean absolute residuals against the measured forest attributes also had implications for the number of images needed to be collected. The model for ![]() had negative coefficients for both BA and DBH, which showed that the percentual errors were largest in young forests with small BA and DBH. Forests representing these conditions were usually seedling stands or pine bogs, where trees are sparsely located, leaving large gaps in between. Thus, forests with large azimuthal variations in gap fractions at the hinge angle are relatively the most difficult targets for the proposed LAI estimation approach. When
had negative coefficients for both BA and DBH, which showed that the percentual errors were largest in young forests with small BA and DBH. Forests representing these conditions were usually seedling stands or pine bogs, where trees are sparsely located, leaving large gaps in between. Thus, forests with large azimuthal variations in gap fractions at the hinge angle are relatively the most difficult targets for the proposed LAI estimation approach. When ![]() was the response variable of instead of
was the response variable of instead of ![]() , the coefficient for BA became positive, i.e. the largest absolute errors occurred in forests with large BA that usually also have a large LAI.
, the coefficient for BA became positive, i.e. the largest absolute errors occurred in forests with large BA that usually also have a large LAI.
Because forest structure clearly has an effect on estimation accuracy, it could be beneficial to utilize existing forest information available online (e.g., metsaan.fi service available in Finland) to adjust the data collection requirements specifically for each site. As alternative, the app could also calculate standard error of the mean for LAI in each location and suggest that more data need to be collected, if the uncertainty is too large.
Nevertheless, special training may be required to ensure that data collected by citizen scientists is sufficiently rigorous for research usage. Training plays a crucial role in underpinning the success of CS projects. Obtaining quality data from trained citizen scientists has been demonstrated possible (Newman et al. 2010) and training methods may further enhance the data quality (Ratnieks et al. 2016). Nevertheless, it should be noted that all data, whether collected by professionals or non-professionals, is subject to biases. It is therefore important to be aware of these biases and proceed carefully in data analysis regardless of data source.
Various AI models, encompassing machine learning (Saoud et al. 2020) and deep learning (Willi et al. 2019) architectures, have been specifically utilised to conduct image analysis tasks – such as object detection and identification – using images sourced from CS projects (Ceccaroni et al. 2019). Thematic segmentation i.e., separating forest canopy from the background sky in our case, represents another prevalent task undertaken by AI models, yet its application to data collected through CS projects remains relatively limited. A recent example showcased the application of deep learning models for agriculture LAI estimation using RGB images (Castro-Valdecantos et al. 2022). With our proposed forest canopy images crowd-sourced by citizen scientists, there is an opportunity to further evaluate the efficacy of AI models within the CS arena.
4.3 Options for gamification
Based on our simulation results and a recent forest gamification study (Nummenmaa et al. 2024), we propose a gamification approach in which citizen scientists are guided to take forest canopy images through gameful steps with the objective of obtaining reliable LAI data. In the cited study, players attempted to catch spiders moving on forest surfaces by pointing at them with the phone camera, facilitating a simultaneous collection of LiDAR data on the structure of trees. In our proposed game, instead of using moving spiders, a flying bird would appear between forest canopies to direct citizen scientists’ attention and help them find the targeted hinge angle. Birds are natural inhabitants commonly spotted in the forest and can fly in any area of the hemisphere. The purpose of this intuitive design is to enable citizen scientists to have an on-screen interplay that prompts them to locate the areas of interest and take canopy images with their mobile devices as an engaging and entertaining activity. Their task is to take an image each time they spot the bird in forest canopy. In return, the game offers the players the recreational experience of passing time, and it can also be integrated into other location-based experiences, such as geocaching. While rewards such as certificates have stimulated participants’ interest in our previous experience, introducing new incentives, including monetary rewards, may further encourage and sustain their engagement.
In the game, citizen scientists can traverse freely within the 12.5-metre radius of forest plot and the game should limit participants within the plot boundary based on the positioning signals of their mobile devices. The location of the simulated bird (φ, θ) can be recorded as azimuth (φ) and zenith (θ) angles, with the magnetic north set as azimuth 0°. As the desired image should be centred at the hinge angle, the simulated zenith angle θ should be fixed at 57° off zenith while the azimuth angle φ can be randomly simulated (Fig. 7). As a result, it is possible to manipulate the locations where the birds would appear and instruct citizen scientists to direct the cameras of their mobile devices at the correct inclination angle. Once the citizen scientist captures the first image, the other three canopy images can be taken at the same location following the flying bird’s movement at 90° azimuth intervals (Scenario 4). To achieve better accuracy, citizen scientists can be instructed to move to another four locations within the plot boundary and conduct the same measures (Scenario 18). There exists a trade-off between achieving accuracy and the risk of data collection becoming overly repetitive. Considering the effectiveness of CS projects in mobilising a large number of participants, the data accumulated would be substantial even if each individual contributes to only one dataset following the requirements of Scenario 18. Nevertheless, this design could be determined by the gamified CS project based on the specific research outcome they aim to achieve.
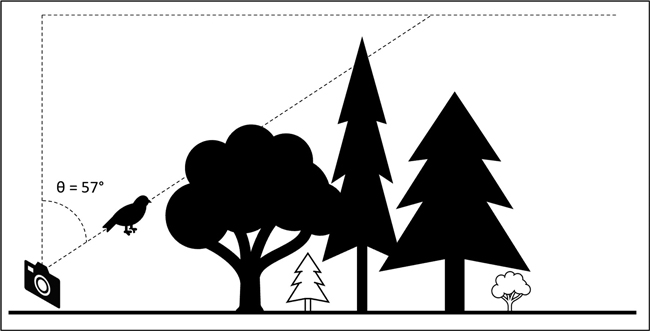
Fig. 7. Illustration of citizen scientists taking images at the hinge angle (θ = 57°) following gamified instructions. A bird will appear on the screen of the smartphone screen to help participants to locate the angle and capture images.
The current study utilised simulation data aiming to provide practical guidance for a forthcoming gamified CS project set in a forest context. As Nature (2015) stated that “technology can make scientists of us all”, and indeed, it constantly shapes the ecology of the research landscape and influences the design and implementation of our upcoming project. This influence included both data collection, such as providing portable consumer-grade smartphone cameras for participants, and data analysis, potentially involving image processing with AI models to instantly segment forest canopy gaps.
Conclusions
We recommend integration of gamification into forthcoming citizen science projects to encourage participants to collect forest leaf area index measurements for research purposes. Data collected this way can be used, for example, to calibrate remote sensing based LAI maps into local conditions. Gamified data collection can help to guide citizen scientists into desired locations and collect high-quality LAI measurements in the way set by the researchers. Our simulations suggest that collecting 20 forest canopy images at the hinge angle can provide a satisfactory accuracy for this purpose. Collecting four images at 90° azimuth intervals is a viable alternative if productivity is preferred instead of accuracy. The next steps are to organize a real gamified LAI data collection project, and test how much calibration with such measurements can improve the accuracy of remotely sensed LAI maps.
Authors’ contributions
Conceptualization (S.Z.; L.K.; T.M.; S.B.; M.M.), data curation (S.Z; L.K.) data analysis (S.Z; L.K.; M.M.), original draft preparation (S.Z.; L.K.; T.M.; S.B.; M.M.), visualization (S.Z.), reviewing and editing, (S.Z.; L.K.; T.M.; S.B.; M.M.), project administration (M.M.). All authors agreed with and contributed equally to the published version of the manuscript.
Declaration of openness of research materials, data, and code
Data and codes are openly published at https://doi.org/10.5281/zenodo.13236565 and https://github.com/UEFshzhang/SimulateIMG57.
Acknowledgements
We thank Juha Inkilä and Laura Kakkonen for data collection in Hyytiälä, as well as Zhongyu Xia and Aapo Erkkilä for assistance in image processing. We thank the managing editor and the anonymous reviewer for their valuable feedback that helped us to improve the manuscript.
Funding
This research was funded by the Research Council of Finland through the Flagship Programme “Forest-Human-Machine Interplay-Building Resilience, Redefining Value Networks and Enabling Meaningful Experiences (UNITE)” under Grant 337127, Grant 357906 and Grant 357907, as well as through the Project “Estimation of forest area and above-ground biomass using spaceborne LiDAR data” under Grant 332707 and the Project “Gamified augmented reality applications for observing trees and forests using LiDAR (GamiLiDAR)” under Grant 359472.
References
Arietta AZA (2022) Estimation of forest canopy structure and understory light using spherical panorama images from smartphone photography. Forestry 95: 38–48. https://doi.org/10.1093/forestry/cpab034.
Calders K, Origo N, Disney M, Nightingale J, Woodgate W, Armston J, Lewis P (2018) Variability and bias in active and passive ground-based measurements of effective plant, wood and leaf area index. Agr Forest Meteorol 252: 231–240. https://doi.org/10.1016/j.agrformet.2018.01.029.
Castro-Valdecantos P, Apolo-Apolo OE, Pérez-Ruiz M, Egea G (2022) Leaf area index estimations by deep learning models using RGB images and data fusion in maize. Precis Agric 23: 1949–1966. https://doi.org/10.1007/s11119-022-09940-0.
Ceccaroni L, Bibby J, Roger E, Flemons P, Michael K, Fagan L, Oliver JL (2019) Opportunities and risks for citizen science in the age of artificial intelligence. Citiz Sci 4, article id 29. https://doi.org/10.5334/cstp.241.
Cescatti A (2007) Indirect estimates of canopy gap fraction based on the linear conversion of hemispherical photographs. Agr Forest Meteorol 143: 1–12. https://doi.org/10.1016/j.agrformet.2006.04.009.
Chen JM, Black TA (1992) Defining leaf area index for non-flat leaves. Plant Cell Environ 15: 421–429. https://doi.org/10.1111/j.1365-3040.1992.tb00992.x.
Chen JM, Cihlar J (1995) Plant canopy gap-size analysis theory for improving optical measurements of leaf-area index. Appl Optics 34: 6211–6222. https://doi.org/10.1364/AO.34.006211.
Coffin D (2008) DCRAW: decoding raw digital photos in linux. https://www.dechifro.org/dcraw/.
Confalonieri R, Foi M, Casa R, Aquaro S, Tona E, Peterle M, Boldini A, De Carli G, Ferrari A, Finotto G, Guarneri T, Manzoni V, Movedi E, Nisoli A, Paleari L, Radici I, Suardi M, Veronesi D, Bregaglio S, Cappelli G, Chiodini ME, Domininoni P, Francone C, Frasso C, Stella T, Acutis M (2013) Development of an app for estimating leaf area index using a smartphone. Trueness and precision determination and comparison with other indirect methods. Comput Electron Agr 96: 67–74. https://doi.org/10.1016/j.compag.2013.04.019.
Crocker E, Condon B, Almsaeed A, Jarret B, Nelson CD, Abbott AG, Main D, Staton M (2020) TreeSnap: a citizen science app connecting tree enthusiasts and forest scientists. Plants People Planet 2: 47–52. https://doi.org/10.1002/ppp3.41.
Crocker E, Gurung K, Calvert J, Nelson CD, Yang J (2023) Integrating GIS, remote sensing, and citizen science to map oak decline risk across the Daniel Boone National Forest. Remote Sens 15, article id 2250. https://doi.org/10.3390/rs15092250.
de Groot M, Pocock MJO, Bonte J, Fernandez-Conradi P, Valdés-Correcher E (2022) Citizen science and monitoring forest pests: a beneficial alliance? Curr For Rep 9: 15–32. https://doi.org/10.1007/s40725-022-00176-9.
de Wit CT (1965) Photosynthesis of leaf canopies. Agricultural research reports 663. Wageningen University. https://library.wur.nl/WebQuery/wurpubs/413358.
Díaz GM, Negri PA, Lencinas JD (2021) Toward making canopy hemispherical photography independent of illumination conditions: a deep-learning-based approach. Agr Forest Meteorol 296, article id 108234. https://doi.org/10.1016/j.agrformet.2020.108234.
Dickinson JL, Zuckerberg B, Bonter DN (2010) Citizen science as an ecological research tool: challenges and benefits. Annu Rev of Ecol Evol Syst 41: 149–172. https://doi.org/10.1146/annurev-ecolsys-102209-144636.
GCOS (2022) The 2022 GCOS implementation plan.
Hanssen KH, Solberg S (2007) Assessment of defoliation during a pine sawfly outbreak: calibration of airborne laser scanning data with hemispherical photography. For Ecol Manag 250: 9–16. https://doi.org/10.1016/j.foreco.2007.03.005.
Kaha M, Lang M, Zhang S, Pisek J (2023) Note on the compatibility of ICOS, NEON, and TERN sampling designs, different camera setups for effective plant area index estimation with digital hemispherical photography. For Stud 79: 21–36. https://doi.org/10.2478/fsmu-2023-0010.
Kobori H, Dickinson JL, Washitani I, Sakurai R, Amano T, Komatsu N, Kitamura W, Takagawa S, Koyama K, Ogawara T, Miller‐Rushing AJ (2016) Citizen science: a new approach to advance ecology, education, and conservation. Ecol Res 31: 1–19. https://doi.org/10.1007/s11284-015-1314-y.
Korhonen L, Heikkinen J (2009) Automated analysis of in situ canopy images for the estimation of forest canopy cover. Forest Sci 55: 323–334. https://doi.org/10.1093/forestscience/55.4.323.
Lang M, Nilson T, Kuusk A, Pisek J, Korhonen L, Uri V (2017) Digital photography for tracking the phenology of an evergreen conifer stand. Agr Forest Meteorol 246: 15–21. https://doi.org/10.1016/j.agrformet.2017.05.021.
Macfarlane C, Hoffman M, Eamus D, Kerp N, Higginson S, McMurtrie R, Adams M (2007) Estimation of leaf area index in eucalypt forest using digital photography. Agr Forest Meteorol 143: 176–188. https://doi.org/10.1016/j.agrformet.2006.10.013.
Majasalmi T, Rautiainen M, Stenberg P, Rita H (2012) Optimizing the sampling scheme for LAI-2000 measurements in a boreal forest. Agr Forest Meteorol 154–155: 38–43. https://doi.org/10.1016/j.agrformet.2011.10.002.
Miller J (1967) A formula for average foliage density. Aust J Bot 15, article id 141. https://doi.org/10.1071/BT9670141.
Moorthy SMK, Calders K, Vicari MB, Verbeeck H (2019) Improved supervised learning-based approach for leaf and wood classification from LiDAR point clouds of forests. IEEE T Geosci Remote 58: 3057–3070. https://doi.org/10.1109/TGRS.2019.2947198.
Nature (2015) Rise of the citizen scientist. Nature 524, article id 265. https://doi.org/10.1038/524265a.
Neumann HH, Den Hartog G, Shaw RH (1989) Leaf area measurements based on hemispheric photographs and leaf-litter collection in a deciduous forest during autumn leaf-fall. Agr Forest Meteorol 45: 325–345. https://doi.org/10.1016/0168-1923(89)90052-X.
Newman G, Crall A, Laituri M, Graham J, Stohlgren T, Moore JC, Kodrich K, Holfelder KA (2010) Teaching citizen science skills online: implications for invasive species training programs. Appl Environ Educ Commun 9: 276–286. https://doi.org/10.1080/1533015X.2010.530896.
Nummenmaa T, Laato S, Chambers P, Yrttimaa T, Vastaranta M, Buruk OT, Hamari J (2024) Employing gamified crowdsourced close-range sensing in the pursuit of a digital twin of the earth. Int J Hum-Comput Int. https://doi.org/10.1080/10447318.2024.2352922.
Purdy LM, Sang Z, Beaubien E, Hamann A (2023) Validating remotely sensed land surface phenology with leaf out records from a citizen science network. Int J Appl Earth Obs 116, article id 103148. https://doi.org/10.1016/j.jag.2022.103148.
Qu Y, Wang J, Song J, Wang J (2017) Potential and limits of retrieving conifer leaf area index using smartphone-based method. Forests 8, article id 217. https://doi.org/10.3390/f8060217.
Qu Y, Wang Z, Shang J, Liu J, Zou J (2021) Estimation of leaf area index using inclined smartphone camera. Comput Electron Agr 191, article id 106514. https://doi.org/10.1016/j.compag.2021.106514.
Ratnieks FLW, Schrell F, Sheppard RC, Brown E, Bristow OE, Garbuzov M (2016) Data reliability in citizen science: learning curve and the effects of training method, volunteer background and experience on identification accuracy of insects visiting ivy flowers. Methods Ecol Evol 7: 1226–1235. https://doi.org/10.1111/2041-210X.12581.
Roy HE, Pocock MJO, Preston CD, Roy DB, Savage J (2012) Understanding citizen science and environmental monitoring: final report on behalf of UK Environmental Observation Framework. https://www.ceh.ac.uk/sites/default/files/citizensciencereview.pdf.
Ryu Y, Nilson T, Kobayashi H, Sonnentag O, Law BE, Baldocchi DD (2010) On the correct estimation of effective leaf area index: does it reveal information on clumping effects? Agr Forest Meteorol 150: 463–472. https://doi.org/10.1016/j.agrformet.2010.01.009.
Ryu Y, Baldocchi DD, Kobayashi H, van Ingen C, Li J, Black TA, Beringer J, van Gorsel E, Knohl A, Law BE, Roupsard O (2011) Integration of MODIS land and atmosphere products with a coupled-process model to estimate gross primary productivity and evapotranspiration from 1 km to global scales. Global Biogeochem Cy 25, article id GB4017. https://doi.org/10.1029/2011GB004053.
Saoud Z, Fontaine C, Loïs G, Julliard R, Rakotoniaina I (2020) Miss-identification detection in citizen science platform for biodiversity monitoring using machine learning. Ecol Inform 60, article id 101176. https://doi.org/10.1016/j.ecoinf.2020.101176.
Silvertown J (2009) A new dawn for citizen science. Trends Ecol Evol 24: 467–471. https://doi.org/10.1016/j.tree.2009.03.017.
Skidmore AK, Pettorelli N, Coops NC, Geller GN, Hansen M, Lucas R, Mücher CA, O’Connor B, Paganini M, Pereira HM, Schaepman ME, Turner W, Wang T, Wegmann M (2015) Environmental science: agree on biodiversity metrics to track from space. Nature 523: 403–405. https://doi.org/10.1038/523403a.
Vastaranta M, Wulder MA, Hamari J, Hyyppä J, Junttila S (2022) Forest data to insights and experiences using gamification. Front For Glob Change 5, article id 799346: https://doi.org/10.3389/ffgc.2022.799346.
Wang H, Wu Y, Ni Q, Liu W (2022) A novel wireless leaf area index sensor based on a combined u-net deep learning model. IEEE Sens J 22: 16573–16585. https://doi.org/10.1109/JSEN.2022.3188697.
Welles JM, Norman JM (1991) Instrument for indirect measurement of canopy architecture. Agron J 83: 818–825. https://doi.org/10.2134/agronj1991.00021962008300050009x.
Willi M, Pitman RT, Cardoso AW, Locke C, Swanson A, Boyer A, Veldthuis M, Fortson L (2019) Identifying animal species in camera trap images using deep learning and citizen science. Methods Ecol Evol 10: 80–91. https://doi.org/10.1111/2041-210X.13099.
Wilson JW (1963) Estimation of foliage denseness and foliage angle by inclined point quadrats. Aust J Bot 11: 95–105. https://doi.org/10.1071/BT9630095.
Yan G, Hu R, Luo J, Weiss M, Jiang H, Mu X, Xie D, Zhang W (2019) Review of indirect optical measurements of leaf area index: recent advances, challenges, and perspectives. Agr Forest Meteorol 265: 390–411. https://doi.org/10.1016/j.agrformet.2018.11.033.
Yang J, Xing D, Luo X (2021) Assessing the performance of a citizen science project for monitoring urban woody plant species diversity in China. Urban For Urban Gree 59, article id 127001. https://doi.org/10.1016/j.ufug.2021.127001.
Yuan H, Dai Y, Xiao Z, Ji D, Shangguan W (2011) Reprocessing the MODIS leaf area index products for land surface and climate modelling. Remote Sens Environ 115: 1171–1187. https://doi.org/10.1016/j.rse.2011.01.001.
Zhang S, Korhonen L, Lang M, Pisek J, Díaz GM, Korpela I, Xia Z, Haapala H, Maltamo M (2024) Comparison of semi-physical and empirical models in the estimation of boreal forest leaf area index and clumping with airborne laser scanning data. IEEE T Geosci Remote 62, article id 5701212. https://doi.org/10.1109/TGRS.2024.3353410.
Zhao K, Ryu Y, Hu T, Garcia M, Li Y, Liu Z, Londo A, Wang C (2019) How to better estimate leaf area index and leaf angle distribution from digital hemispherical photography? Switching to a binary nonlinear regression paradigm. Methods Ecol Evol 10: 1864–1874. https://doi.org/10.1111/2041-210X.13273.
Total of 49 references.

