Effects of Scots pine paternal genotypes of two contiguous seed orchards on the budset and frost hardening of first-year progeny
Lehtinen M. T., Pulkkinen P. (2017). Effects of Scots pine paternal genotypes of two contiguous seed orchards on the budset and frost hardening of first-year progeny. Silva Fennica vol. 51 no. 5 article id 7783. https://doi.org/10.14214/sf.7783
Highlights
- This environmentally controlled study on Scots pine demonstrated the effect of the paternal genotype on the budset and frost hardening of the progeny
- With the applied study design, no significant indication of an environmental influence on the effect of the Scots pine paternal genotype was obtained.
Abstract
In Scots pine (Pinus sylvestris L.), it has been shown that the parental conditions have a role in the phenological variation among first-year seedlings. For this reason, it is argued that they should be comprehensively controlled before estimating the parental genotype effects. This controlled-cross study examined the effects of a set of fathers of Scots pines on the timing of budset and autumn frost hardening of first-year seedlings. The paternal genotypes had either a northern or southern provenance, but had spent a period of over 25 years as grafts in a shared climatic environment in two closely located southern orchards. Pollen applied in the crosses was collected from these orchards in one year and all the maternal genotypes were pollinated in only one seed orchard. The results of freeze tests and budset observations of the consequent progeny were analysed and additionally compared with results obtained using seedlings from seed lots of natural forests in order to estimate the ability of northern paternal genotypes to maintain a northern effect under southern conditions. This environmentally controlled study demonstrated a significant effect of the paternal genotype on the budset and autumn frost hardening of first-year seedling of Scots pine. With the applied study design, no significant indication of an environmental influence on the effect of the paternal genotype was obtained. The accuracy of the observations is discussed. It is concluded that the results suggest a minor role of mutability in the effects of Scots pine paternal genotypes.
Keywords
Pinus sylvestris;
provenance;
conifer;
environmental influence;
pollen;
genotype effect
-
Lehtinen,
University of Helsinki, Department of Agricultural Sciences, Latokartanonkaari 5 and 7, P.O. Box 27, FI-00014 University of Helsinki, Finland
E-mail
markku.t.lehtinen@helsinki.fi

- Pulkkinen, Natural Resources Institute Finland (Luke), Green Technology, Haapastensyrjäntie 34, FI-12600 Läyliäinen, Finland E-mail pertti.pulkkinen@luke.fi
Received 3 August 2017 Accepted 30 October 2017 Published 7 November 2017
Views 101343
Available at https://doi.org/10.14214/sf.7783 | Download PDF

1 Introduction
There has been considerable progress in recent years in understanding the genetic mechanisms underlying the regulation of important phenological traits in plants (Andres and Coupland 2012). The first steps were achieved among angiosperm model species, but recent studies dealing, for example, with conifer homologues of photoperiod pathway genes (Kujala and Savolainen 2012; Chen et al. 2012, 2014, 2016; Avia et al. 2014; Källman et al. 2014) have added gymnosperms to the list. Draft genome assemblies of Norway spruce (Nystedt et al. 2013) and Loblolly pine (Wegrzyn et al. 2014) have revealed a major role of transposable elements in the genome structure of conifers. This finding, combined with a growing understanding concerning small RNA-directed epigenetic regulation (Henderson and Jacobsen 2007) and the nature of transposons as driving factors of genome diversification and evolution or gene regulation (Voronova 2014; Grandbastien 2015), has created a novel basis to understand the potential of the conifer genome to respond to environmental challenges. Because epigenetic changes might be long term and heritable (Henderson and Jacobsen 2007), and a response through the mobilization of transposable elements might not actualize until the next generation (Komatsu et al. 2003; Madsen et al. 2005; Fukai et al. 2010), the parental environment is an important covariate to take into account when considering the factors affecting phenological variation among conifer descendants.
Scots pine (Pinus sylvestris L.) is a conifer species with a wide distribution range in northern Eurasia and the Mediterranean region (Mirov 1967). Populations are found in and adapted to a wide range of environmental conditions (Savolainen et al. 2011; Kujala and Savolainen 2012). Phenological adaptation through the timing of vegetative growth actualizes well in the timing of terminal budset and autumn frost hardening of first-year seedlings. Among the first-year seedlings of northern populations of Scots pine, these two traits follow latitudinal clines (Mikola 1982; Aho 1994; Hurme et al. 1997).
The climatic adaptation of northern Scots pine seedlings through budset timing under the control of a combination of the temperature sum and critical night length (Oleksyn et al. 1992) has been proven to be governed by the genetic properties of the parent trees (Mikola 1982; Savolainen et al. 2004). The initiation of autumn frost hardening has also clearly been observed to be determined by the genetic properties of the parent trees (Aho 1994; Savolainen et al. 2004). The inheritance of these traits has additionally been demonstrated through the detection of several potential quantitative trait loci (QTL), some of them with a large effect (Hurme et al. 2000; Yazdani 2003). These findings have been established through controlled crosses (Yazdani 2003), outcrosses (Savolainen et al. 2004) or both (Mikola 1982; Aho 1994; Hurme et al. 2000), with multiple parental environments that must have been taken into consideration as potential covariates. However, specifically in those cases where several controlled crosses have been conducted by applying freeze-preserved pollen originating from multiple orchards or growing seasons, inheritance might have become defined through test designs in which only the maternal environment has been thoroughly controlled both spatially and temporally.
In Norway spruce (Picea abies (L.) Karst.), the parental environment has been observed to have a considerable effect on the phenology of seedlings (Johnsen et al. 2005; Kvaalen and Johnsen 2007; Skrøppa et al. 2007). The effect has also been demonstrated in other spruce species (Webber et al. 2005). Similarly, in Scots pine, an effect of the parental environment on progeny performance has been detected (Dormling and Johnsen 1992), although there are indications that the effect is small (Ruotsalainen et al. 1995). In view of the dynamic and unique epigenetic control observed in the angiosperm male germ lineage (Russel and Jones 2015), these several findings among gymnosperms indicate the possibility that the paternal conditions in Scots pine might have a role in the phenological variation among first-year seedlings, and for this reason should be comprehensively controlled before estimating the genotype effect.
There are indications concerning spruce species that environmental conditions during microspore genesis to pollen shedding have no effect on progeny performance (Johnsen et al. 1996; Webber et al. 2005). However, these findings regarding springtime reproductive events do not rule out the potential role of the paternal conditions in the phenology of Scots pine seedlings. Namely, the initiation of male generative tissue formation in spruce and pine already takes place in the previous growing season. In addition, in connection with this fact, the male generative tissue overwinters at the archesporial stage in Scots pine (Koski 1991), but at the further advanced premeiotic stage in spruce species (Owens and Molder 1977; Harrison and Owens 1983). Thus, due to these temporal and species-specific factors, the above-mentioned results do not provide a basis for further conclusions. Moreover, the conditions encountered by pollen during the period between anthesis and fertilization would play a more significant role as a covariate of the results in surveys regarding Scots pine than they played in the study on spruce by Johnsen et al. (1996). This is because the male gametophytic period in the ovule of the maternal tree lasts over a year in Scots pine (Håkansson 1956) compared to some weeks in spruce (Sarvas 1964).
The primary aim of this study on Scots pine was to estimate the exclusive genotype effect of the fathers on the timing of budset and frost hardening of first-year seedlings. There was interest in completely removing the effect of the divergent paternal environment as a source of variation. The controlled-cross paternal genotypes of this study had either a northern or southern origin, but had nevertheless spent a period of over 25 years as grafts in a shared climatic environment in two closely located southern orchards. Pollination and subsequent reproductive events of the controlled-cross maternal genotypes took place under shared conditions in a single southern seed orchard location. Through shared conditions during the sporophytic and gametophytic periods, differentiated external factors could be excluded as a source of dissimilar genetic or epigenetic changes in parental cells, gametophytic cells, zygotes or embryonic cells, and hence they could also be excluded as a source of divergent gametophytic or sporophytic selection. Additionally, the corresponding conditions among the maternal genotypes excluded differentiated external factors as a source of dissimilar physiological events among the seeds.
The quarter-century history of the northern paternal genotypes in the southern seed orchard conditions provided a platform to explore the influence of the environment on the effect of the genotype. Thus, another objective of this study was to detect the mutability of the effect of the paternal genotype. A change in the effect of northern paternal genotypes was sought by looking for a change in the provenance effect of the orchard genotypes. The null hypothesis was that the provenance effect of the paternal genotypes in the southern seed orchards does not differ from that of paternal genotypes in natural forests.
The pollen of Scots pine spends an approximately thirteen-month period as pollen grains or pollen tubes in the ovules of the maternal tree (Håkansson 1956). In the case of the pollen transported with air currents from distant locations, this phase of the gametophytic period takes place under the influence of novel climatic conditions. The latter objective of the study offered a tool to define the role of a non-native reproductive environment in the ability of distant pollen to convey its native characteristics to progeny.
2 Material and methods
The budset and frost hardening of first-year Scots pine seedlings from seeds produced in crosses and obtained from natural forests were examined. The paternal genotypes applied in the controlled crosses belonged to either southern (S) or northern (N) populations. The paternal genotypes had experienced shared environmental conditions, as had the maternal genotypes. Seedlings from the seed lots of natural forests were included in this study as standard material to demonstrate the existing effect of parental locality on progeny performance. The observed effect of locality was then applied in examining the ability of northern paternal genotypes of southern orchards to maintain the effect of provenance.
2.1 Controlled crosses
Controlled crosses were conducted by applying a factorial mating design (Table 1). Grafts of three maternal genotypes, growing in a single ten-year-old seed orchard in Ahvenlampi in central Finland (62°45´N, 25°10´E, 140 m a.s.l.), were cross-pollinated with pollen from grafts of seven paternal genotypes growing in one of two seed orchards (62°04´N or 62°10´N) in Korpilahti, central Finland. Each of the cross-combinations used one randomly selected graft of the maternal genotype, and for each paternal genotype, one graft was used as the source of the pollen. The crosses were executed in a single year, during the final days of May in 2013.
| Table 1. Information on the crosses conducted in the Ahvenlampi Scots pine seed orchard in 2013. Grafts of three maternal genotypes were cross-pollinated with pollen from seven paternal genotypes from two other Scots pine orchards and pollen from surrounding forests. The cross-combinations with the original genotype codes, the genotype provenance effective temperature sums (d.d.) plus latitudes and the genotype codes applied in the tables and figures are listed. The letters of the genotype codes denote the following: E, K and P = southern, central and northern Finland, respectively; M = maternal genotype; S = southern paternal genotype; N = northern paternal genotype; OP = southern pollen mixture from forests surrounding the orchard of the controlled crosses. | ||||
| Cross-combination maternal * paternal genotype with the original codes | Maternal genotype provenance d.d. and (latitude) | Paternal genotype provenance d.d. and (latitude) | Applied maternal genotype code | Applied paternal genotype code |
| K205 Open pollinated | 1095 (62°34´) | 1075 (62°45´) | M1 | OP |
| K205 * K543 | 1095 (62°34´) | 1049 (62°50´) | M1 | S1 |
| K205 * K652 | 1095 (62°34´) | 1112 (62°22´) | M1 | S2 |
| K205 * K890 | 1095 (62°34´) | 1090 (62°50´) | M1 | S3 |
| K205 * P573 | 1095 (62°34´) | 692 (68°33´) | M1 | N1 |
| K205 * P575 | 1095 (62°34´) | 692 (68°33´) | M1 | N2 |
| K205 * P577 | 1095 (62°34´) | 692 (68°33´) | M1 | N3 |
| K205 * P625 | 1095 (62°34´) | 692 (68°33´) | M1 | N4 |
| K214B Open pollinated | 1117 (62°37´) | 1075 (62°45´) | M2 | OP |
| K214B * K543 | 1117 (62°37´) | 1049 (62°50´) | M2 | S1 |
| K214B * K652 | 1117 (62°37´) | 1112 (62°22´) | M2 | S2 |
| K214B * K890 | 1117 (62°37´) | 1090 (62°50´) | M2 | S3 |
| K214B * P573 | 1117 (62°37´) | 692 (68°33´) | M2 | N1 |
| K214B * P575 | 1117 (62°37´) | 692 (68°33´) | M2 | N2 |
| K214B * P577 | 1117 (62°37´) | 692 (68°33´) | M2 | N3 |
| K214B * P625 | 1117 (62°37´) | 692 (68°33´) | M2 | N4 |
| E2856 Open pollinated | 1142 (62°02´) | 1075 (62°45´) | M3 | OP |
| E2856 * K543 | 1142 (62°02´) | 1049 (62°50´) | M3 | S1 |
| E2856 * K652 | 1142 (62°02´) | 1112 (62°22´) | M3 | S2 |
| E2856 * K890 | 1142 (62°02´) | 1090 (62°50´) | M3 | S3 |
| E2856 * P573 | 1142 (62°02´) | 692 (68°33´) | M3 | N1 |
| E2856 * P575 | 1142 (62°02´) | 692 (68°33´) | M3 | N2 |
| E2856 * P577 | 1142 (62°02´) | 692 (68°33´) | M3 | N3 |
| E2856 * P625 | 1142 (62°02´) | 692 (68°33´) | M3 | N4 |
The provenance of four of the paternal genotypes was the Lake Inari district in northernmost Finland (68°33´N), with an average effective temperature sum of 692 (annual sum of daily mean temperatures that exceed 5 °C; degree days or d.d.). The provenances of the remaining three paternal genotypes were districts in central Finland (62°22´N–62°50´N), with average effective temperature sums of 1049–1112. The provenances of all three maternal genotypes were also districts in central Finland (62°02´N–62°37´N), with average effective temperature sums of 1095–1142 (Table 1).
All grafts of all seven paternal genotypes had grown since 1972 or 1973 in one of two closely located orchards (62°04´N, 25°27´E, 200 m a.s.l., Myrtillus/Vaccinium-type forest or 62°10´N, 25°21´E, 170 m a.s.l., Myrtillus/Vaccinium-type forest) in Korpilahti, central Finland. The pollen applied in the crosses was collected from these orchards in one year, 1999. Since all grafts of all the maternal genotypes were pollinated in one seed orchard, the mature seed cones were collected from a single geographic location in late October 2014.
2.2 Open-pollinated seeds as reference material
Since the Ahvenlampi orchard did not yet produce its own male strobili, a large mixture of paternal pollen from surrounding stands formed the paternal population. There was an interest in comparing the paternal effect of surrounding stands (1075 d.d.) with the effects of the southern paternal genotypes (1049–1112 d.d.) of controlled crosses. Thus, at the same time as the controlled-cross seed cones were harvested, open-pollinated (OP) seed cones of the maternal genotypes were additionally collected (Table 1).
2.3 Natural Scots pine forest seeds as standard material
As part of the study, first-year seedlings from seed lots of eight Scots pine natural forest stands of the Natural Resources Institute Finland (Luke) and from seed lots of the forest management company Tapio Ltd from three Scots pine forest areas were also observed and tested to yield standard values for comparison with the results obtained using seedlings from the seeds of controlled crosses. The harvesting area for the standard seed material has not been consistent and the ripening year of a seed lot depends on the locality (Table 2). The effective temperature sum values and latitudes of the forest localities presented in Table 2 are in three cases mean values for several places in the locality, and not exact values for a particular stand. While recognizing the inconsistent background of the temperature sum values, the lots were nevertheless applied in this study in statistical analysis. As seen in Table 2, the effective temperature sum values ranged between forests from 760 to 1275, and the forests were geographically scattered from southern Finland (60°58´N) to northern Finland (67°22´N).
| Table 2. Information concerning the natural Scots pine forests included in this study as a source of seed material. The forest locality, latitude, effective temperature sum (d.d.) and ripening year of the seed lot are listed. | |||
| Forest locality | Latitude | d.d. | Ripening year |
| Kittilä | 67°22´ | 760 | 1988 |
| Pello | 66°48´ | 860 | 1988 |
| Puolanka | 65°05´ | 880 | 1997 |
| Pudasjärvi | 65°35´ | 900 | 1997 |
| Suomussalmi | 64°57´ | 980 | 1991 |
| Pyhäjärvi | 63°34´ | 1000 | 1997 |
| Lestijärvi | 63°39´ | 1020 | 1991 |
| Rautavaara | 63°28´ | 1050 | 2002 |
| Keuruu | 62°16´ | 1100 | 2003 |
| Korpilahti | 61°55´ | 1150 | 1997 |
| Rauma | 60°58´ | 1275 | 2002 |
2.3 Freezing test
Autumn frost hardening was evaluated based on the growing, chilling and freezing of seedlings under artificial conditions at the Haapastensyrjä Unit (60°62´N, 24°43´E) of the Natural Resources Institute Finland (Luke).
The sowing, growing and chilling of seedlings was carried out in a fully computerized greenhouse. The seeds of each cross-combination were sown as an eight-seedling row plot in eight different boxes (60 × 40 × 8 cm; filled with a pre-fertilized Sphagnum peat block), each of which belonged to a different randomized complete block (replicate). If the initial number of seeds per cross-combination was lower than 64, as was case in four out of the twenty-four combinations, five-seedling row plots were sown in 4–8 boxes. The average germeability of controlled-cross seeds was 96.0%. The total number of yielded controlled-cross seedlings was 1170, while the average number of seedlings per cross combination was 56. Natural forest seeds were sown in the same manner in the same replicates as the controlled-cross seeds, but the number of row plots was doubled and the average number of yielded seedlings per forest was 107. The seedlings were grown for 10 weeks with a 19 h 50 min day and a 4 h 10 min night at respective temperatures of 22 °C and 15 °C.
The growing period was followed by a chilling period of nearly six weeks with shortening day lengths and decreasing temperatures. Chilling was initiated by decreasing the day temperature to 16 °C and delaying the start of the day by 45 min, and five days later by decreasing the night temperature to 8 °C and ending the day 35 min earlier. Three days after this, the day temperature was first lowered by 2 °C and the start of the day was delayed for 45 min and then, half a week later, the night temperature was lowered by 1 °C and the end of the day was brought forward by 45 min. This was repeated every week for the next three weeks. When a minimum chilling temperature of 10 °C in the day and 5 °C at night had been reached, the start of the night was moved 45 min earlier twice a week, but the start of the day remained unchanged.
After the first two weeks of chilling of all the replicates, each replicate in turn was exposed to frost in an air-cooled freezing chamber during a four-week period at a rate of two replicates per week. The initial temperature in the freezing chamber was +5 °C and the cooling rate was 3 °C h–1. The minimum temperature of –10 °C was maintained for two hours and was followed by thawing at a rate of 3 °C h–1 until the initial temperature of +5 °C was reached. After exposure to frost, the replicates were moved back to the chilling conditions.
Two weeks after the freezing treatment, the frost damage of seedlings was measured by observing the colour of the primary needles. Damage was evaluated by recording the coverage of browning according to one of seven percentages: 0%, 10%, 30%, 50%, 70%, 90% or 100% coverage. The percentage browning of primary needles (variable: Br %) was applied in this study as a measure of the autumn frost hardiness of the seedlings.
2.4 Budset observations
The budset timing of seedlings was determined by detecting the phenological response to natural conditions. Observations took place in the facilities at the Haapastensyrjä Unit (60°62´N, 24°43´E) of the Natural Resources Institute Finland (Luke).
Sowing was performed on 10 May. Seeds from each of eleven natural forests and twenty-four cross-combinations were sown as eight-seedling row plots in eight boxes (60 × 40 × 8 cm; filled with a pre-fertilized Sphagnum peat block), each of which belonged to a different randomized complete block (replicate). If the initial number of seeds per cross-combination was lower than 64, as was case in ten out of twenty-four combinations, two- to five-seedling row plots were sown in eight boxes. The mean germeability of the controlled-cross seeds was 91.1%. The total number of yielded controlled-cross seedlings was 893, while the mean number of seedlings per cross-combination was 43. In the case of the natural forests, two seeds per hole were sown. If both seeds sprouted, the right-hand seedling was removed. The mean number of seedlings yielded per forest was 62. For the first eight weeks, the seedlings were grown in a greenhouse compartment in which the temperature and photoperiod followed the ambient conditions at Haapastensyrjä. Thereafter, from July, the seedlings were kept outdoors.
From the end of July (week 30) to late September (week 38), the appearance of terminal buds was checked once a week. The timing of budset of the seedlings was recorded as the calendar week when the terminal buds appeared (variable: Week).
2.5 Statistics
The freezing test and budset observation results are graphically presented as values for individual seedlings. In the parametric tests on groups, the values for individual seedlings were replaced with the statistical means for sets of seedlings. These sets of seedlings were formed by combining the following pairs of replicates: 1 and 8, 2 and 7, 3 and 6, and 4 and 5. In this way, normal distributions within and equal error variances across groups were achieved, although two of the six tests could be seen as borderline cases in this regard, since Levene’s test indicated unequal error variances with P = 0.030 and P = 0.029.
Statistical tests were performed by applying the GLM Univariate procedure of SPSS statistical software. The following three models were applied in the tests:
![]()
, where the dependent variable Y represents the value for Week or Br %, the fixed factor M represents the maternal genotype, the fixed factor P represents the paternal genotype and M*P represents the interaction between maternal and paternal genotypes. Model 1 was applied to detect the effect of the paternal genotype on the timing of budset and frost hardening of controlled-cross seedlings. Tukey’s post hoc test was conducted in the model to provide quantitative effect estimations between paternal genotypes, indicated as a mean difference value. In the post hoc tests, the paternal genotype OP was also included in the data.
![]()
, where the dependent variable Y represents the value for Week or Br % and the independent variable Ldd is the average effective temperature sum at the natural forest location and corresponds to the locality. Model 2 was applied to quantify the effect of the natural forest locality on the timing of budset and frost hardening of first-year seedlings. The quantity is determined through the regression coefficient of the variable Ldd (βLdd) in the model.
![]()
, where the dependent variable Y represents the value for Week or Br %, the fixed factor M represents the maternal genotype and the covariate Pdd is the average effective temperature sum at the original location of the paternal genotype and corresponds to the provenance of the paternal genotype. Model 3 was applied to quantify the effect of the paternal genotype provenance on the timing of budset and frost hardening of controlled-cross seedlings. The quantity is determined through the regression coefficient of the variable Pdd (βPdd) in the model.
The regression coefficient estimates of the variables Ldd and Pdd derived from Models 2 and 3 were further applied to detect the difference in the provenance effect between the paternal genotypes of the natural forests and the paternal genotypes of the southern seed orchards. The study hypothesis was that the environment in a southern orchard might influence the effect of a northern father on the budset and frost hardening of the progeny, and consequently the detected proportion of the provenance effect that comes from the paternal genotype in controlled crosses would be below half of the detected locality effect brought by both sexes in natural forest populations. The null hypothesis (H0) was that the provenance effect of the paternal genotype in the southern seed orchard is equal to the provenance effect of the paternal genotype in the natural forest, and the regression coefficient of Pdd (βPdd) and half of the regression coefficient of Ldd (0.5*βLdd) do not differ.
![]()
Eq. 4 includes the expectation that variation in the phenology of the first-year progeny of Scots pine comes equally from both parents. In addition, the use of βLdd in the equation includes an assumption of linear dependence between the effective temperature sum and the first-year seedling performance throughout the target geographic region. The linear nature of the temperature sum effect was checked.
Since the variance of residuals of Model 3 (σModel32) included the impact of the heterozygosity of the maternal genotype and, on the other hand, the variance of residuals of Model 2 (σModel22) included the impact of the population, there were no equal residual variances when comparing βPdd and 0.5*βLdd. Consequently, in this study, instead of a parametric test, the significance of the difference between βPdd and 0.5*βLdd was examined by comparing the 95% confidence intervals of both. The confidence interval of 0.5*βLdd was inferred as follows: If the effects of the actual heterozygous maternal genotypes are replaced with the effect of just a single hypothetical homozygous maternal genotype, the covariance (SXY) of the observational data (xi, yi), of the independent variable X and dependent variable Y will then be halved in such a way that in each observation (xi, yi), the new yi deviates from the new ymean half as much as the original yi deviated from the original ymean. From this, it follows that the estimate of the regression coefficient β [b = SXY*(SX2)–1] (Ranta et al. 1989) will be halved, and SQR(SY.X2), where SY.X2 [MSresidual=((n–1)SY2–((n–1)SXY)2*((n–1)SX2)–1)*(n–2)–1] (Ranta et al. 1989) is the estimator of the common variance of the residuals of the model (estimator of σModel2), will be halved. From the latter, it follows that the standard error of b [Sb=SQR(SY.X2*((n–1)SX2)–1)] (Ranta et al. 1989) will also be halved. As a final outcome, the confidence interval of 0.5*β can be expressed as [0.5*b – 2*0.5*Sb , 0.5*b + 2*0.5*Sb] if the original confidence interval of β was in the form of [b – 2*Sb , b + 2*Sb].
3 Results
The paternal genotypes applied in this study had a clear effect on the timing of budset and autumn frost hardening of first-year seedlings (Table 3). Typically, the effect (mean difference) was statistically significant between paternal genotypes with northern and southern origins, but in quite many cases, the effect was even significant between paternal genotypes with the same geographical origin (Table 4).
| Table 3. Results from the ANOVA tests (Model 1). The tests investigated the effect of the Scots pine paternal genotype on the timing of budset (Week) and autumn frost hardening (Br %) of first-year seedlings. Model 1: Y = Intercept + M + P + M*P, where Y = Week or Br %; M = maternal genotype; P = paternal genotype. | ||||||
| Dependent variable: Week | Dependent variable: Br % | |||||
| df | F | Sig. | df | F | Sig. | |
| Corrected model | 20 | 11.058 | <0.001 | 20 | 7.264 | <0.001 |
| Intercept | 1 | 274849.954 | <0.001 | 1 | 2951.919 | <0.001 |
| Maternal genotype | 2 | 19.581 | <0.001 | 2 | 7.889 | 0.001 |
| Paternal genotype | 6 | 26.370 | <0.001 | 6 | 19.676 | <0.001 |
| Maternal genotype * Paternal genotype | 12 | 1.981 | 0.041 | 12 | 0.894 | 0.558 |
| Error | 63 | 60 | ||||
| df = the number of degrees of freedom; F = F ratio; Sig. = p-value; Week = the calendar week when the terminal buds appeared; Br % = the percentage browning of primary needles. | ||||||
| Table 4. Tukey post hoc test results for the ANOVA tests (Model 1). Pairwise comparisons of the paternal genotype effect (mean difference) on the timing of budset (Week) and autumn frost hardening (Br %) of first-year seedlings of Scots pine. OP, N1–N4 and S1–S3 are codes for the paternal genotypes. The letters of the codes denote the following: S = southern paternal genotype; N = northern paternal genotype; OP = southern pollen mixture from forests surrounding the orchard of the controlled crosses. | |||||||
| Dependent variable: Week | Dependent variable: Br % | ||||||
| (I) Paternal genotype | (J) Paternal genotype | Mean difference (I-J) | p-value | Signi- ficance | Mean difference (I-J) | p-value | Signi- ficance |
| OP | N1 | 1.313 | <0.001 | *** | 23.548 | <0.001 | *** |
| N2 | –0.077 | 1.000 | 39.812 | <0.001 | *** | ||
| N3 | 2.322 | <0.001 | *** | 24.480 | <0.001 | *** | |
| N4 | 1.199 | <0.001 | *** | 29.038 | <0.001 | *** | |
| S1 | –0.203 | 0.991 | 0.942 | 1.000 | |||
| S2 | 0.735 | 0.072 | –0.425 | 1.000 | |||
| S3 | 0.491 | 0.495 | 13.663 | 0.060 | |||
| N1 | N2 | –1.389 | <0.001 | *** | 16.264 | 0.009 | ** |
| N3 | 1.009 | 0.003 | ** | 0.933 | 1.000 | ||
| N4 | –0.113 | 1.000 | 5.490 | 0.912 | |||
| S1 | –1.516 | <0.001 | *** | –22.606 | <0.001 | *** | |
| S2 | –0.578 | 0.285 | –23.973 | <0.001 | *** | ||
| S3 | –0.822 | 0.028 | * | –9.885 | 0.358 | ||
| N2 | N3 | 2.398 | <0.001 | *** | –15.332 | 0.017 | * |
| N4 | 1.276 | <0.001 | *** | –10.774 | 0.228 | ||
| S1 | –0.127 | 1.000 | –38.870 | <0.001 | *** | ||
| S2 | 0.812 | 0.031 | * | –40.237 | <0.001 | *** | |
| S3 | 0.568 | 0.307 | –26.149 | <0.001 | *** | ||
| N3 | N4 | –1.123 | 0.001 | *** | 4.558 | 0.966 | |
| S1 | –2.525 | <0.001 | *** | –23.538 | <0.001 | *** | |
| S2 | –1.587 | <0.001 | *** | –24.905 | <0.001 | *** | |
| S3 | –1.831 | <0.001 | *** | –10.817 | 0.248 | ||
| N4 | S1 | –1.403 | <0.001 | *** | –28.096 | <0.001 | *** |
| S2 | –0.464 | 0.567 | –29.463 | <0.001 | *** | ||
| S3 | –0.708 | 0.093 | –15.375 | 0.021 | * | ||
| S1 | S2 | 0.938 | 0.007 | ** | –1.367 | 1.000 | |
| S3 | 0.694 | 0.107 | 12.721 | 0.101 | |||
| S2 | S3 | –0.244 | 0.974 | 14.088 | 0.067 | ||
| ***p-value < 0.001, **p-value < 0.01, *p-value < 0.05; Week = the calendar week when the terminal buds appeared; Br % = the percentage browning of primary needles. | |||||||
The largest detected effect of the paternal genotype on the timing of budset (Week) and autumn frost hardiness (Br %), respectively, was 2.53 and 40.24 if examined among southern and northern origins, 2.40 and 16.26 if examined among paternal genotypes with a northern origin alone, and 0.94 and 14.09 if examined among those with a southern origin (Table 4).
Fig. 1 presents the mean Week and Br % values of the examined seedlings by cross-combination. Cross-combinations are grouped by the three maternal genotypes (M1–M3), and groups are further arranged alphabetically according to the paternal genotype code. Fig. 1 clearly shows the effect of geographical origin (OP and S = southern; N = northern) of the paternal genotype on the budset and frost hardiness of the seedlings. In the case of budset (Week), however, the effect is not uniform across the paternal genotypes (Fig. 1a). Specifically, the mean Week values of cross-combinations with the northern paternal genotype N2 have the same order of magnitude as those of cross-combinations involving southern (S1–S3) paternal genotypes (Fig. 1a). Regarding the frost hardiness (Br %) of the seedlings, the effect of the geographical origin of the paternal genotype is more consistent (Fig. 1b). Only in the case of the southern paternal genotype S3 is the effect less apparent. The findings of Fig. 1 can also be seen from the mean difference values of the pairs of southern reference genotype OP in Table 4.
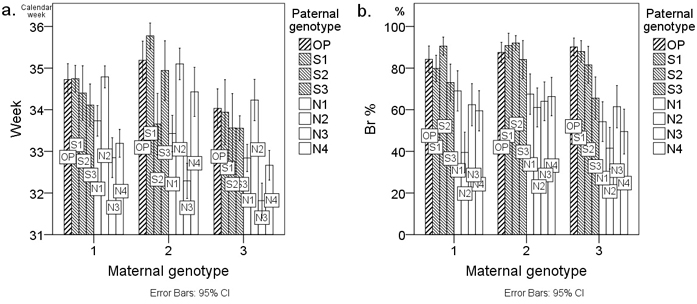
Fig. 1. Average a. timing of budset (Week) and b. frost hardiness (Br %) of first-year Scots pine seedlings from twenty-four cross-combinations presented as bar charts. Cross-combinations (columns) are grouped by the three maternal genotypes M1–M3 on the x-axis. Cross-combinations are labelled with the paternal genotype code. The letters of the paternal genotype codes denote the following: S = southern paternal genotype; N = northern paternal genotype; OP = southern pollen mixture from forests surrounding the orchard of the controlled crosses. Week denotes the calendar week when the terminal buds appeared and Br % denotes the percentage browning of primary needles. Error bars represent the 95% confidence intervals.
In cross-combinations with the paternal genotype N2, the high southern Week values (Fig. 1a) were not reflected by the high southern Br % values (Fig. 1b). Each cross-combination involving the paternal genotype N2 exhibited Br % values of the low northern type (Fig. 1b). The northern effect of the paternal genotype N2 was statistically significant, not only between southern paternal genotypes S1–S3, but even between northern paternal genotypes N1 and N3 (Table 4).
The locality of the parental forest, indicated by the temperature sum value in this study (Ldd; Model 2), explained, as expected, the performance of the Scots pine seedlings. This was demonstrated by the statistical significance of the regression coefficient of Ldd (βLdd). The coefficient obtained was statistically significant both in the case of budset (Week) and frost hardening (Br %) of the first-year seedlings (Table 5). Regression coefficient estimates of 0.0057 and 0.160 for Ldd (see B in Table 5) predict that each 100-degree-day transition to the south in the position of the natural forest results in a 0.57 higher Week value for the timing of terminal budset and a 16.0 higher Br % value for the frost hardiness of the seedlings.
| Table 5. Results from the linear regression analyses (Model 2). The analyses quantified the effect of the parental forest locality (Ldd) on the timing of budset (Week) and frost hardening (Br %) of first-year Scots pine seedlings. Model 2: Y = Intercept + Ldd, where Y = Week or Br %; Ldd = average effective temperature sum at the natural forest location. | |||||||
| Dependent variable: Week | Dependent variable: Br % | ||||||
| ANOVA | ANOVA | ||||||
| df | F | p-value | df | F | p-value | ||
| Regression | 1 | 136.104 | <0.001 | Regression | 1 | 140.091 | <0.001 |
| Residual | 42 | Residual | 42 | ||||
| Coefficients | Coefficients | ||||||
| Model | Unstandardized coefficients | Model | Unstandardized coefficients | ||||
| B | SE | p-value | B | SE | p-value | ||
| (Constant) | 28.982 | 0.488 | <0.001 | (Constant) | –103.522 | 13.597 | <0.001 |
| Ldd | 0.0057 | 0.0005 | <0.001 | Ldd | 0.160 | 0.013 | <0.001 |
| df = the number of degrees of freedom; F = F ratio; B = estimate; SE = estimate standard error; Week = the calendar week when the terminal buds appeared; Br % = the percentage browning of primary needles. | |||||||
The provenance effect of the paternal genotypes, with the provenance indicated by the effective temperature sum value at the location (Pdd), was quantified in Model 3. Paternal genotypes of the controlled crosses growing in one of the two southern (central Finland) seed orchards as grafts showed a significant effect of the provenance on the timing of budset and frost hardening of first-year progeny. The effect was expressed through the regression coefficient of the covariate Pdd (βPdd), and the coefficient was statistically significant in the case of both Week and Br % (Table 6). The coefficient estimates of 0.002 and 0.062 for Pdd (see B in Table 6) predict that each 100-degree-day transition to the south in the position of the provenance of the paternal genotype results in a 0.2 higher Week value for the timing of terminal budset and a 6.2 higher Br % value for the frost hardiness of the first-year seedlings. The relative significance of the covariate Pdd as a source of variation is indicated through the partial eta squared value. Partial eta squared values of 0.153 and 0.486 for Pdd (Table 6) in Week and Br %, respectively, indicate that the provenance of the paternal genotype is more significant as a source of variation in the case of autumn frost hardening than it is in the case of the timing of budset of the seedlings. This conclusion is concordant with observations from Fig. 1.
| Table 6. Results from the ANCOVA tests (Model 3). Model 3 was applied to quantify the effect of the paternal genotype provenance on the timing of budset (Week) and autumn frost hardening (Br %) of controlled-cross Scots pine seedlings. Model 3: Y = Intercept + M + Pdd, where Y = Week or Br %; M = maternal genotype; Pdd = average effective temperature sum at the original location of the paternal genotype, which corresponds to the provenance of the paternal genotype. | |||||||||||||||
| Dependent variable: Week | Dependent variable: Br % | ||||||||||||||
| Tests of between-subject effects | Tests of between-subject effects | ||||||||||||||
| Source | df | F | p-value | Partial Eta Squared | Source | df | F | p-value | Partial Eta Squared | ||||||
| Corrected Model | 3 | 9.868 | <0.001 | 0.270 | Corrected Model | 3 | 28.445 | <0.001 | 0.526 | ||||||
| Intercept | 1 | 4644.29 | <0.001 | 0.983 | Intercept | 1 | 5.529 | 0.021 | 0.067 | ||||||
| Pdd | 1 | 14.498 | <0.001 | 0.153 | Pdd | 1 | 72.706 | <0.001 | 0.486 | ||||||
| Maternal genotype | 2 | 7.553 | 0.001 | 0.159 | Maternal genotype | 2 | 6.598 | 0.002 | 0.146 | ||||||
| Error | 80 | Error | 77 | ||||||||||||
| Parameter estimates | Parameter estimates | ||||||||||||||
| Parameter | B | SE | p-value | Parameter | B | SE | p-value | ||||||||
| Intercept | 31.515 | 0.493 | <0.001 | Intercept | 9.606 | 6.721 | 0.157 | ||||||||
| Pdd | 0.002 | 0.0005 | <0.001 | Pdd | 0.062 | 0.007 | <0.001 | ||||||||
| df = the number of degrees of freedom; F = F ratio; Partial Eta Squared = SSEffect*(SSEffect + SSError)–1, SS = sum of squares; B = coefficient estimate; SE = estimate standard error; Week = the calendar week when the terminal buds appeared; Br % = the percentage browning of primary needles. | |||||||||||||||
Half of the initial regression coefficient of variable Ldd from Model 2 (0.5*βLdd) and the regression coefficient of variable Pdd from Model 3 (βPdd) was applied in this study to detect the difference in the provenance effect between the paternal genotypes of the natural forests and the paternal genotypes of the southern seed orchards. The 95% confidence intervals of 0.5*βLdd and βPdd clearly overlap for both Week and Br % (see Fig. 2). Consequently, the results of the present study indicate that the provenance effect of the paternal genotype in the southern seed orchard is equal to that in the natural forest.
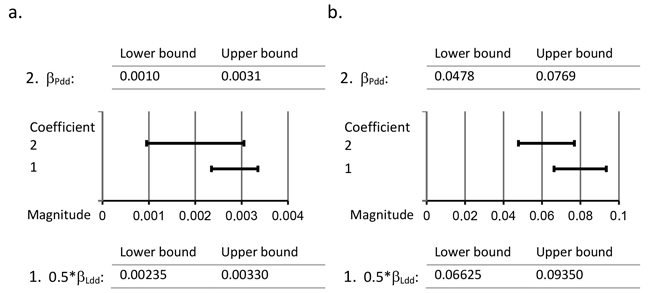
Fig. 2. Comparison of 95% confidence intervals of regression coefficients 0.5*βLdd and βPdd. Detection of the difference in the provenance effect between the Scots pine paternal genotypes of the natural forests and the paternal genotypes of the southern seed orchards by comparing the 95% confidence intervals of 0.5*βLdd and βPdd in the case of a. the timing of budset (Week) and b. frost hardening (Br %) of first-year seedlings. 0.5*βLdd denotes half of the regression coefficient of the independent variable Ldd from Model 2, where Ldd is the average effective temperature sum at the natural forest locality; βPdd denotes the regression coefficient of the covariate Pdd from Model 3, where Pdd is the average effective temperature sum at the original location of the seed orchard paternal genotype.
4 Discussion
This study demonstrated a significant effect of the paternal genotype on the budset and frost hardening of first-year seedling of Scots pine. A study design was applied where all mothers shared common conditions at all stages of their life cycle, as did all fathers. In the case of the timing of budset, the study indicated that the paternal genotype effect might be as marked within a provenance as between provenances separated by a distance of 400 degree days, the effects being 2.4 weeks and 2.5 weeks, respectively. Regarding autumn frost hardening, this study demonstrated the importance of provenance as a factor determining the paternal genotype effect. The largest browning percentage effect of 40.24% between fathers of different provenances compared to 16.26% among fathers of same provenance, as well as the high partial eta squared value of 0.486 for Pdd, clearly illustrates the importance of provenance.
The budset and frost hardening of first-year seedlings were examined not only from controlled-cross seeds but also from natural forest seeds with the aim of detecting the influence of the seed orchard environment on the effect of the northern Scots pine paternal genotype. The results indicated that the provenance effect of the paternal genotype in the southern seed orchard was equal to the provenance effect of the paternal genotype in the natural forest, and this study was consequently unable to demonstrate an influence of the southern environment on the effect of the northern paternal genotype.
The supposed influence of the environment on the effect of the paternal genotype may originate from multiple causes. Findings from Arabidopsis thaliana (L.) Heynh. indicate the inheritability of environmental stress-induced epigenetic changes (Whittle et al. 2009; Migicovsky et al. 2014), and this phenomenon might similarly appear among conifer species. The influence of the surrounding environment may also occur through gametophytic or sporophytic selection (Webber et al. 2005), and gametophytic selection has also been supposed to affect the progeny performance of conifers (Owens et al. 2001; Schmidtling and Hipkins 2004).
In this study, the search for a change in the effect of the northern paternal genotype was, in principle, a comparison of populations. In connection with this aspect, it should be noted that the seven paternal genotypes comprised a small set of representatives for the entire tree populations of two separate provenances. A direct consequence of the small number of genotypes was the wide confidence interval of the regression coefficient βPdd, which did not allow the observation of small effect changes. It is worth remarking that to some extent, both in the case of budset and frost hardening, the value of the estimate of βPdd was less than half of the value obtained for the estimate of βLdd, suggesting some type of change in the northern father effect. Consequently, the results of this study do not exclude the possibility of a change in the effect of the paternal genotype.
Not only the quantitative matter mentioned above, but also some qualitative and theoretical issues may have affected the accuracy of the results of this study. The consequences of these issues are not consistent, they are related to either a false indication of the stagnancy of the paternal genotype effect or to unfounded indications of its mutability.
First, there has inevitably been a difference in the conditions of seed ripening between the northern and southern standard forests; the average effective temperature sum difference between the forest locations has been up to 515 d.d. (Table 2). Hypothetically, the poorer seed quality of the northern forests compared to southern ones may have led to a decreased difference in frost hardiness between the seedlings originating from different locations and further to an incorrect indication of the stagnant frost hardiness of controlled-cross genotypes. On the other hand, it appears that such a case is unlikely, since at least Andersson (1989) and Dormling and Johnsen (1992) were unable in their studies to demonstrate an effect of seed weight on the frost hardiness of first-year seedlings of Scots pine.
Secondly, the attempt to obtain statistical proof of an environment influence on the northern paternal effect was based on quite a simplified assumption that as much as half of the phenological variation among seedlings of a natural forest population comes from fathers. Indeed, this view is supported by a study by Mikola (1982), who found that the budset of Scots pine progeny appeared to be equally determined by both parent trees. However, it is worth noting that non-Mendelian cytoplasmic inheritance, which is discussed by Bruns and Owens (2000), among others, might alter the proportional effects of the two sexes. Additionally, the results from A. thaliana suggest that the newly acquired stress-induced epigenetic marks are more efficiently reset in male than in female gametes, and are therefore preferentially transmitted through the female germline (Wibowo et al. 2016). Assuming that the restoration of lost paternal epigenetic marks is partially guided by maternal siRNA in the embryo, (Calarco et al. 2012), the maternal party may have more than an equal role in the phenological variation of the progeny. If the true effect of a Scots pine father is less than half, the assumption of equal effects applied in this study favours the generation of false indications of an effect change.
Third, the paternal and maternal genotypes applied in the crosses were grafts from plus trees of Finnish breeding programmes. It has been suggested that plus tree selection might favour genotypes with a prolonged growth period (Andersson 1985), and this might explain the results of this study concerning the timing of budset. The progeny of northern paternal genotype N2 in the present study expressed a northern frost tolerance but a southern timing of budset. If this observed feature actually stems from plus tree selection, the effect of N2 distorted the results in this study. Moreover, the phenotypic plus tree selection may generate genetic diversity not only equal to (Skrøppa 1994; Funda and El-Kassaby 2012) but even greater than that of a natural forest population (Chaisurisri and El-Kassaby 1994), and this fact might explain the results of this study concerning frost hardening. If the frost hardiness of the progeny of paternal genotype S3 associates with the increased allelic or genetic diversity of a plus tree population, the effect of S3 resulted in an inappropriate estimate of the provenance effect of the original populations.
In the controlled crosses of the present study, gametophytic and later sporophytic selection only took place among the pollen and embryos of one paternal genotype. This is suitable for evaluating the influence of the environment on the effect of northern fathers, but due to the lack of competition with pollen of other paternal genotypes, it reduces the reliability of the study in proving the capability of distant pollen in natural circumstances to affect the phenology of the resulting seedlings. A study performed through artificial crosses with pollen mixtures has detected signs of pollen competition in Scots pine (Pulkkinen et al. 2009), although another study has reported no observable competition (Varis et al. 2008). In any case, the results of the present study indicate that the abiotic environment as such does not significantly reduce the capability of distant pollen to affect the phenology of the progeny. It should be noted that the northern genotype unnaturally represented the gene flow in this study. Southerly winds have been observed to predominate at the time of pollination in Finland (Sarvas 1962; Koski 1970), and northern populations of Scots pine normally flower later than southern ones (Giertych and Mátyás 1991).
As a conclusion, the results of this study indicate a significant paternal genotype effect on the budset and frost hardening of first-year seedlings of Scots pine. With the applied study design, no significant indication of an environmental influence on the effect of the genotype was obtained. Taking into account the above-mentioned qualitative and theoretical issues in the design of this study, which could generate unfounded indications of a northern father effect change, the results suggest a minor role of mutability in the effects of Scots pine paternal genotypes.
Acknowledgements
The authors thank Aulis Leppänen, Minna Mäkinen and Marja-Liisa Tölmälä from the Haapastensyrjä Research Station of the Natural Resources Institute Finland (Luke) for their invaluable effort in implementing this research.
References
Aho M-L. (1994). Autumn frost hardening of one-year-old Pinus sylvestris L. seedlings: effect of origin and parent trees. Scandinavian Journal of Forest Research 9(1–4): 17–24. https://doi.org/10.1080/02827589409382808.
Andersson B. (1985). Freezing tests of northern Scots pine seedlings from seed orchards. In: Nilsson J-E. (ed.). Reforestation material for harsh northern sites. Proceedings of the seminar at Umeå. Swedish University of Agricultural Sciences Department of Forest Genetics and Plant Physiology. Report 4. p. 42–56. [In Swedish with English summary].
Andersson B. (1989). Effect of maternal soil treatment on first year growth and autumn frost hardiness of Pinus sylvestris L. full-sib families. Scandinavian Journal of Forest Research 4(1–4): 163–173. https://doi.org/10.1080/02827588909382555.
Andres F., Coupland G. (2012). The genetic basis of flowering responses to seasonal cues. Nature Reviews Genetics 13: 627–639. https://doi.org/10.1038/nrg3291.
Avia K., Kärkkäinen K., Lagercrantz U., Savolainen O. (2014). Association of FLOWERING LOCUS T/TERMINAL FLOWER1-like gene FTL2 expression with growth rhythm in Scots pine (Pinus sylvestris). New Phytologist 204(1): 159–170. https://doi.org/10.1111/nph.12901.
Bruns D., Owens J.N. (2000). Western white pine (Pinus monticola Dougl.) reproduction: II. Fertilisation and cytoplasmic inheritance. Sexual Plant Reproduction 13(2): 75–84. https://doi.org/10.1007/s004970000041.
Calarco J.P., Borges F., Donoghue M.T.A., Van Ex F., Jullien P.E., Lopes T., Gardner R., Berger F., Feijó J.A., Becker J.D., Martienssen R.A. (2012). Reprogramming of DNA methylation in pollen guides epigenetic inheritance via small RNA. Cell 151(1): 194–205. https://doi.org/10.1016/j.cell.2012.09.001.
Chaisurisri K., El-Kassaby Y.A. (1994). Genetic diversity in a seed production population vs. natural populations of Sitka spruce. Biodiversity and Conservation 3(6): 512–523. https://doi.org/10.1007/BF00115157.
Chen J., Källman T., Ma X-F., Gyllenstrand N., Zaina G., Morgante M., Bousquet J., Eckert A., Wegrzyn J., Neale D., Lagercrantz U., Lascoux M. (2012). Disentangling the roles of history and local selection in shaping clinal variation of allele frequencies and gene expression in Norway spruce (Picea abies). Genetics 191(3): 865–881. https://doi.org/10.1534/genetics.112.140749.
Chen J., Tsuda Y., Stocks M., Källman T., Xu N., Kärkkäinen K., Huotari T., Semerikov V.L., Vendramin G.G., Lascoux M. (2014). Clinal variation at phenology-related genes in spruce: parallel evolution in FTL2 and Gigantea? Genetics 197(3): 1025–1038. https://doi.org/10.1534/genetics.114.163063.
Chen J., Källman T., Ma X-F., Zaina G., Morgante M., Lascoux M. (2016). Identifying genetic signatures of natural selection using pooled population sequencing in Picea abies. G3 Genes Genomes Genetics 6(7): 1979–1989. https://doi.org/10.1534/g3.116.028753.
Dormling I., Johnsen Ø. (1992). Effects of the parental environment on full-sib families of Pinus sylvestris. Canadian Journal of Forest Research 22(1): 88–100. https://doi.org/10.1139/x92-013.
Fukai E., Umehara Y., Sato S., Endo M., Kouchi H., Hayashi M., Stougaard J., Hirochika H. (2010). Derepression of the plant chromovirus LORE1 induces germline transposition in regenerated plants (germline retrotransposition of a plant chromovirus). PLoS Genetics 6(3): e1000868. https://doi.org/10.1371/journal.pgen.1000868.
Funda T., El-Kassaby Y.A. (2012). Seed orchard genetics. CAB reviews: perspectives in agriculture, veterinary science, nutrition and natural resources 7(13). 23 p.
Giertych M., Mátyás Cs. (1991). Genetics of Scots Pine. Elsevier Science Publishers, Amsterdam. ISBN 044498724X.
Grandbastien M-A. (2015). LTR retrotransposons, handy hitchhikers of plant regulation and stress response. Biochimica et Biophysica Acta – Gene Regulatory Mechanisms 1849(4): 403–416. https://doi.org/10.1016/j.bbagrm.2014.07.017.
Håkansson A. (1956). Seed development of Picea abies and Pinus sylvestris. Meddelanden från statens skogsforskningsinstitut 46(2). 23 p.
Harrison D.L.S., Owens J.N. (1983). Bud development in Picea engelmannii. I. Vegetative bud development, differentiation, and early development of reproductive buds. Canadian Journal of Botany 61(9): 2291–2301. https://doi.org/10.1139/b83-251.
Henderson I.R., Jacobsen S.E. (2007). Epigenetic inheritance in plants. Nature 447: 418–424. https://doi.org/10.1038/nature05917.
Hurme P., Repo T., Savolainen O., Pääkkönen T. (1997). Climatic adaptation of bud set and frost hardiness in Scots pine (Pinus sylvestris L.). Canadian Journal of Forest Research 27(5): 716–723. https://doi.org/10.1139/x97-052.
Hurme P., Sillanpää M.J., Arjas E., Repo T., Savolainen O. (2000). Genetic basis of climatic adaptation in Scots pine by Bayesian quantitative trait locus analysis. Genetics 156(3): 1309–1322.
Johnsen Ø., Skrøppa T., Junttila O., Dæhlen O.G. (1996). Influence of the female flowering environment on autumn frost-hardiness of Picea abies progenies. Theoretical and Applied Genetics 92(7): 797–802. https://doi.org/10.1007/BF00221890.
Johnsen Ø., Fossdal C.G., Nagy N., Mølmann J., Dæhlen O.G., Skrøppa T. (2005). Climatic adaptation in Picea abies progenies is affected by the temperature during zygotic embryogenesis and seed maturation. Plant, Cell & Environment 28(9): 1090–1102. https://doi.org/10.1111/j.1365-3040.2005.01356.x.
Källman T., De Mita S., Larsson H., Gyllenstrand N., Heuertz M., Parducci L., Suyama Y., Lagercrantz U., Lascoux M. (2014). Patterns of nucleotide diversity at photoperiod related genes in Norway spruce [Picea abies (L.) Karst.]. PLoS ONE 9(5): e95306. https://doi.org/10.1371/journal.pone.0095306.
Komatsu M., Shimamoto K., Kyozuka J. (2003). Two-step regulation and continuous retrotransposition of the rice LINE-type retrotransposon Karma. The Plant Cell 15(8): 1934–1944. http://www.jstor.org/stable/3872020.
Koski V. (1970). A study of pollen dispersal as a mechanism of gene flow in conifers. Communicationes Instituti Forestalis Fenniae 70.4. http://urn.fi/URN:NBN:fi-metla-201207171102.
Koski V. (1991). Generative reproduction and genetic processes in nature. In: Giertych M., Matyas C. (eds.). Developments in plant genetics and breeding 3, Genetics of Scots pine. Elsevier Science Publishers, Amsterdam and Akademiai Kiado, Budapest. p. 59–72.
Kujala S.T., Savolainen O. (2012). Sequence variation patterns along a latitudinal cline in Scots pine (Pinus sylvestris): signs of clinal adaptation? Tree Genetics & Genomes 8(6): 1451–1467. https://doi.org/10.1007/s11295-012-0532-5.
Kvaalen H., Johnsen Ø. (2007). Timing of bud set in Picea abies is regulated by a memory of temperature during zygotic and somatic embryogenesis. New Phytologist 177(1): 49–59. https://doi.org/10.1111/j.1469-8137.2007.02222.x.
Madsen L.H., Fukai E., Radutoiu S., Yost C.K., Sandal N., Schauser L., Stougaard J. (2005). LORE1, an active low-copy-number TY3-gypsy retrotransposon family in the model legume Lotus japonicus. The Plant Journal 44(3): 372–381. https://doi.org/10.1111/j.1365-313X.2005.02534.x.
Migicovsky Z., Yao Y., Kovalchuk I. (2014). Transgenerational phenotypic and epigenetic changes in response to heat stress in Arabidopsis thaliana. Plant Signaling & Behavior 9(2): e27971. https://doi.org/10.4161/psb.27971.
Mikola J. (1982). Bud-set phenology as an indicator of climatic adaptation of Scots pine in Finland. Silva Fennica 16(2): 178–184. https://doi.org/10.14214/sf.a15075.
Mirov N.T. (1967). The genus Pinus. Ronald Press, New York.
Nystedt B., Street N.R., Wetterbom A., Zuccolo A., Lin Y-C., Scofield D.G., Vezzi F., Delhomme N., Giacomello S., Alexeyenko A., Vicedomini R., Sahlin K., Sherwood E., Elfstrand M., Gramzow L., Holmberg K., Hällman J., Keech O., Klasson L., Koriabine M. (2013). The Norway spruce genome sequence and conifer genome evolution. Nature 497: 579–584. https://doi.org/10.1038/nature12211.
Oleksyn J., Tjoelker M.G., Reich P.B. (1992). Growth and biomass partitioning of populations of European Pinus sylvestris L. under simulated 50 and 60 N daylengths: evidence for photoperiodic ecotypes. The New Phytologist 120(4): 561–574. http://www.jstor.org/stable/2557418.
Owens J.N., Molder M. (1977). Bud development in Picea glauca. II. Cone differentiation and early development. Canadian Journal of Botany 55(21): 2746–2760. https://doi.org/10.1139/b77-313.
Owens J.N., Johnsen Ø., Dæhlen O.G., Skrøppa T. (2001). Potential effects of temperature on early reproductive development and progeny performance in Picea abies (L.) Karst. Scandinavian Journal of Forest Research 16(3): 221–237. https://doi.org/10.1080/02827580117248.
Pulkkinen P., Varis S., Pakkanen A., Koivuranta L., Vakkari P., Parantainen A. (2009). Southern pollen sired more seeds than northern pollen in southern seed orchards established with northern clones of Pinus sylvestris. Scandinavian Journal of Forest Research 24(1): 8–14. https://doi.org/10.1080/02827580802592467.
Ranta E., Rita H., Kouki J. (1989). Biometria. [Biometry]. Yliopistopaino, Helsinki. 569 p. [In Finnish].
Ruotsalainen S., Nikkanen T., Haapanen M. (1995). Effect of seed-maturing conditions on the growth and hardiness of one-year-old Pinus sylvestris seedlings. Forest Genetics 2: 189–198.
Russell S.D., Jones D.S. (2015). The male germline of angiosperms: repertoire of an inconspicuous but important cell lineage. Frontiers in Plant Science 6 article 173. https://doi.org/10.3389/fpls.2015.00173.
Sarvas R. (1962). Investigations on the flowering and seed crop of Pinus silvestris. Communicationes Instituti Forestalis Fenniae 53.4. http://urn.fi/URN:NBN:fi-metla-201207171085.
Sarvas R. (1964). Havupuut. [Conifers]. WSOY, Porvoo. 518 p. [In Finnish].
Savolainen O., Bokma F., Garcia-Gil M.R., Komulainen P., Repo T. (2004). Genetic variation in cessation of growth and frost hardiness and consequences for adaptation of Pinus sylvestris to climatic changes. Forest Ecology and Management 197(1–3): 79–89. https://doi.org/10.1016/j.foreco.2004.05.006.
Savolainen O., Kujala S.T., Sokol C., Pyhäjärvi T., Avia K., Knurr T., Kärkkäinen K., Hicks S. (2011). Adaptive potential of northernmost tree populations to climate change, with emphasis on Scots pine (Pinus sylvestris L.). Journal of Heredity 102(5): 526–536. https://doi.org/10.1093/jhered/esr056.
Schmidtling R.C., Hipkins V. (2004). The after-effects of reproductive environment in shortleaf pine. Forestry 77(4): 287–295. https://doi.org/10.1093/forestry/77.4.287.
Skrøppa T. (1994) Impacts of tree improvement on genetic structure and diversity of planted forests. Silva Fennica 28(4): 265–274. https://doi.org/10.14214/sf.a9179.
Skrøppa T., Kohmann K., Johnsen Ø., Steffenrem A., Edvardsen Ø.M. (2007). Field performance and early test results of offspring from two Norway spruce seed orchards containing clones transferred to warmer climates. Canadian Journal of Forest Research 37(3): 515–522. https://doi.org/10.1139/X06-253.
Varis S., Santanen A., Pakkanen A., Pulkkinen P. (2008). The importance of being the first pollen in the strobili of Scots pine. Canadian Journal of Forest Research 38(12): 2976–2980. https://doi.org/10.1139/X08-138.
Voronova A., Belevich V., Jansons A., Rungis D. (2014). Stress-induced transcriptional activation of retrotransposon-like sequences in the Scots pine (Pinus sylvestris L.) genome. Tree Genetics & Genomes 10(4): 937–951. https://doi.org/10.1007/s11295-014-0733-1.
Webber J., Ott P., Owens J., Binder W. (2005). Elevated temperature during reproductive development affects cone traits and progeny performance in Picea glauca × engelmannii complex. Tree Physiology 25: 1219–1227. https://doi.org/10.1093/treephys/25.10.1219.
Wegrzyn J.L., Liechty J.D., Stevens K.A., Wu L-S., Loopstra C.A., Vasquez-Gross H.A., Dougherty W.M., Lin B.Y., Zieve J.J., Martinez-Garcia P.J., Holt C., Yandell M., Zimin A.V., Yorke J.A., Crepeau M.W., Puiu D., Salzberg S.L., de Jong P.J., Mockaitis K., Main D., Langley C.H., Neale D.B. (2014). Unique features of the Loblolly pine (Pinus taeda L.) megagenome revealed through sequence annotation. Genetics 196(3): 891–909. https://doi.org/10.1534/genetics.113.159996.
Whittle C.A., Otto S.P., Johnston M.O., Krochko J.E. (2009). Adaptive epigenetic memory of ancestral temperature regime in Arabidopsis thaliana. Botany 87(6): 650–657. https://doi.org/10.1139/B09-030.
Wibowo A., Becker C., Marconi G., Durr J., Price J., Hagmann J., Papareddy R., Putra H., Kageyama J., Becker J., Weigel D., Gutierrez-Marcos J. (2016). Hyperosmotic stress memory in Arabidopsis is mediated by distinct epigenetically labile sites in the genome and is restricted in the male germline by DNA glycosylase activity. eLife 2016(5): e13546. https://doi.org/10.7554/eLife.13546.
Yazdani R., Nilsson J-E., Plomion C., Mathur G. (2003). Marker trait association for autumn cold acclimation and growth rhythm in Pinus sylvestris. Scandinavian Journal of Forest Research 18(1): 29–38. https://doi.org/10.1080/02827581.2003.10383135.
Total of 55 references.

