Estimating coarse roots biomass in young silver birch stands on post-agricultural lands in central Poland
Bijak S., Zasada M., Bronisz A., Bronisz K., Czajkowski M., Ludwisiak Ł., Tomusiak R., Wojtan R. (2013). Estimating coarse roots biomass in young silver birch stands on post-agricultural lands in central Poland. Silva Fennica vol. 47 no. 2 article id 963. https://doi.org/10.14214/sf.963
Highlights
- Age and size of the tree are the most important factors that influence the amount of belowground biomass
- Allocation of the biomass to the coarse roots also depends on age and size of the tree
Abstract
Study analyses coarse (d>2 mm of diameter) roots biomass dynamics in young succession stands of silver birch (Betula pendula Roth) growing on abandoned farmlands in central Poland. Research material based on 181 sample trees, which were gathered in 20 pure silver birch stands in 5 locations. The age of the trees varied from 1 to 16 years. Coarse roots biomass of the investigated trees ranged from 0.7 to 4305.5 g/tree (422.6 g/tree on average) showing great variability (coefficient of variation equals 185%). A clear dependence of belowground biomass on the age and size of a tree was observed. Root-to-shoot ratio values vary from 0.1 to 1.0 with evidence of a tendency to decrease with increasing age, diameter at the breast height and height of analysed trees. An allometric equation was elaborated for the estimation of belowground biomass based on height or diameter at breast height of young silver birches. The suitability of this formula should be considered for the estimation of biomass accumulation and carbon sequestration by young successional silver birch stands growing on abandoned agricultural lands.
Keywords
abandoned farmland;
belowground biomass;
allometric equations;
root-to-shoot ratio
-
Bijak,
Warsaw University of Life Sciences – SGGW, Faculty of Forestry, Laboratory of Dendrometry and Forest Productivity, Nowoursynowska 159, 02-776 Warszawa, Poland
E-mail
szymon.bijak@wl.sggw.pl

- Zasada, Warsaw University of Life Sciences – SGGW, Faculty of Forestry, Laboratory of Dendrometry and Forest Productivity, Nowoursynowska 159, 02-767 Warszawa, Poland E-mail michal.zasada@wl.sggw.pl
- Bronisz, Warsaw University of Life Sciences – SGGW, Faculty of Forestry, Laboratory of Dendrometry and Forest Productivity, Warszawa, Poland E-mail agnieszka.bronisz@wl.sggw.pl
- Bronisz, Warsaw University of Life Sciences – SGGW, Faculty of Forestry, Laboratory of Dendrometry and Forest Productivity, Warszawa, Poland E-mail karol.bronisz@wl.sggw.pl
- Czajkowski, Warsaw University of Life Sciences – SGGW, Faculty of Forestry, Laboratory of Dendrometry and Forest Productivity, Warszawa, Poland E-mail maciej.czajkowski@wl.sggw.pl
- Ludwisiak, Warsaw University of Life Sciences – SGGW, Faculty of Forestry, Laboratory of Dendrometry and Forest Productivity, Warszawa, Poland E-mail lukasz.ludwisiak@wl.sggw.pl
- Tomusiak, Warsaw University of Life Sciences – SGGW, Faculty of Forestry, Laboratory of Dendrometry and Forest Productivity, Warszawa, Poland E-mail robert.tomusiak@wl.sggw.pl
- Wojtan, Warsaw University of Life Sciences – SGGW, Faculty of Forestry, Laboratory of Dendrometry and Forest Productivity, Warszawa, Poland E-mail rafal.wojtan@wl.sggw.pl
Received 9 April 2013 Accepted 28 June 2013 Published 11 July 2013
Views 209207
Available at https://doi.org/10.14214/sf.963 | Download PDF

1 Introduction
Forests are considered to have an essential role in the mitigation of global climate change effects because they are capable of carbon assimilation and sequestration in living tissues (Lorenz and Lal 2010). Accounting for 90% of vegetative carbon in terrestrial biomes and absorbing 67% of total CO2, they are large carbon stores (Gower 2003). Forests being carbon sink or source depends on the balance between this element sequestration and release (Spalding et al. 2012). Managing the forests, and to a greater extent the whole afforested area, plays a crucial role in both of these processes (Carroll et al. 2012). Afforestation/reforestation of abandoned agricultural land is the most common and simple way of increasing the amount of available carbon pools, nevertheless its efficiency under various ecological settings is debated (Guo and Gifford 2002; Uri et al. 2007; Hodgman et al. 2012). The shift in land use from the agricultural field to the forest results in changes affecting different parts of this kind of ecosystem. Such transitions affect the species composition, the biomass of the vegetation, soil properties and carbon sequestration in growing biomass and in the soil (Vesterdal et al. 2007; Hodgman et al. 2012). The transformation of post-agricultural lands towards plantations or forest areas may well be a valuable source of biomass production for energetic purposes or CO2 sequestration. It is crucial therefore to gain knowledge about the possible productivity of such areas.
Changes that occurred in the politics and the economy of Central and Eastern Europe at the end of last century caused a rapid increase in areas of abandoned agricultural lands. Such areas are very often afforested naturally by fast growing pioneer species, e.g. silver birch (Karlsson et al. 1998; Zając and Gil 2003). Taking into account the extension of this phenomenon, it seems to be important as well as urgent to understand how to manage/maintain such areas.
Although silver birch (Betula pendula Roth) is widely distributed in Eurasia, it is most abundant in northern Europe, where birches are the most important commercial broad-leaved tree species (Hynynen et al. 2010). In the Baltic and Nordic countries, the proportion of birch in the total volume of the forest growing stock varies between 11% and 28% (Uri et al. 2012). Silver birch is also an important tree species in Poland, where it occupies ca. 7.5% of the total area of forests (Central Statistical Office 2011).
Quantifying belowground biomass is important for the understanding and estimating of net primary production, biomass partitioning, belowground competition as well as carbon accumulation in forest ecosystems. A review of literature on the biomass of silver birch reveals that studies focus mainly on aboveground biomass (cf. Repola et al. 2007). Mälkönen (1977) analysed the total aboveground biomass production for a forty-year-old birch stand in Finland. In turn, Ferm (1993) evaluated the potential of birch for biomass production in countries with Nordic climate. Johansson (1999) studied the biomass of birch stands growing on abandoned farmland in Sweden. Claesson et al. (2001) elaborated functions for the calculation of biomass in birch stands of high density. Individual tree models for the crown biomass distribution for birch were developed by Tahvanainen and Forss (2008). Recent studies on birch biomass were conducted in Estonia (Kuznetsova et al. 2011; Uri et al. 2007, 2012; Varik et al. 2013) and Finland (Hytönen and Aro 2012). Only a few authors have published functions that allow the estimation of the biomass of belowground components for birch (Petersson and Ståhl 2006; Johansson 2007; Repola et al. 2007; Uri et al. 2007; Repola 2008; Varik et al. 2013). So far there have been no studies on carbon sequestration in birch forests growing on post-agricultural lands in Poland.
The working hypotheses of the presented study assumed that (i) age and size of trees have a significant impact on amount and allocation of belowground biomass of young silver birch stands, and (ii) inclusion of height in allometric equations gives better fit of the biomass estimates. To test these hypotheses, our objectives included (i) assessment of the amount of biomass stored in the belowground parts of young birches growing on post-agricultural lands in central Poland, (ii) elaboration of equations for the estimation of belowground biomass of young birches, and (iii) analysis of the effect of tree age and size on the allocation of biomass to roots.
2 Material and methods
2.1 Study sites
Our study included 20 stands growing on former agricultural lands in five locations in central Poland (Table 1). Plots were established in pure silver birch stands that were supposed to have successional origin. The former farmland status of the selected localities as well as the cessation of agricultural use was checked and confirmed by either the local forest or national park administration. All the investigated stands originated from natural regeneration that started after the farming use was abandoned and remained free from any silvicultural treatments by the time the sample material was collected. The actual stand density was very variable as well as age-dependent, and equalled from ca. 1.55x106 trees/ha in the youngest stands to ca. 3.5x103 trees/ha in the oldest ones.
| Table 1. Characteristics of study sites and mean values of basic sample trees attributes. | |||||||
| Lp. | Site | Location | Soil types | Age [yrs] | dbh [mm] | h [m] | BGB [kg/tree] |
| 1 | Dobieszyn1 | 51°35ʹN, 21°10ʹE | Podzols & luvisols | 2 | 0.2 | 1.03 | 0.015 |
| 2 | Dobieszyn1 | 51°35ʹN, 21°10ʹE | Podzols & luvisols | 5 | 7.0 | 2.20 | 0.027 |
| 3 | Dobieszyn1 | 51°35ʹN, 21°10ʹE | Podzols & luvisols | 9 | 28.2 | 4.97 | 0.499 |
| 4 | Dobieszyn1 | 51°35ʹN, 21°10ʹE | Podzols & luvisols | 13 | 58.2 | 8.61 | 1.771 |
| 5 | Dobieszyn2 | 51°33ʹN, 21°09ʹE | Podzols & luvisols | 4 | 0.0 | 0.64 | 0.003 |
| 6 | Dobieszyn2 | 51°33ʹN, 21°09ʹE | Podzols & luvisols | 6 | 13.9 | 3.26 | 0.073 |
| 7 | Dobieszyn2 | 51°33ʹN, 21°09ʹE | Podzols & luvisols | 7 | 29.1 | 5.15 | 0.241 |
| 8 | Dobieszyn2 | 51°33ʹN, 21°09ʹE | Podzols & luvisols | 12 | 64.1 | 10.24 | 2.141 |
| 9 | Kozienice | 51°24ʹN, 21°26ʹE | Podzols & luvisols | 4 | 0.0 | 0.73 | 0.004 |
| 10 | Kozienice | 51°24ʹN, 21°26ʹE | Podzols & luvisols | 3 | 20.6 | 3.10 | 0.322 |
| 11 | Kozienice | 51°24ʹN, 21°26ʹE | Podzols & luvisols | 12 | 36.8 | 5.95 | 0.326 |
| 12 | Kozienice | 51°24ʹN, 21°26ʹE | Podzols & luvisols | 13 | 56.3 | 9.33 | 1.038 |
| 13 | KPN1 | 52°21ʹN, 20°43ʹE | Luvisols & cambisols | 3 | 0.0 | 0.44 | 0.002 |
| 14 | KPN1 | 52°21ʹN, 20°43ʹE | Luvisols & cambisols | 6 | 16.7 | 3.64 | 0.093 |
| 15 | KPN1 | 52°21ʹN, 20°43ʹE | Luvisols & cambisols | 11 | 35.1 | 5.75 | 0.533 |
| 16 | KPN1 | 52°21ʹN, 20°43ʹE | Luvisols & cambisols | 12 | 60.9 | 8.30 | 1.510 |
| 17 | KPN2 | 52°20ʹN, 20°41ʹE | Luvisols & cambisols | 4 | 1.0 | 1.37 | 0.014 |
| 18 | KPN2 | 52°19ʹN, 20°40ʹE | Luvisols & cambisols | 5 | 16.0 | 3.08 | 0.110 |
| 19 | KPN2 | 52°19ʹN, 20°39ʹE | Luvisols & cambisols | 7 | 25.5 | 4.98 | 0.181 |
| 20 | KPN2 | 52°19ʹN, 20°39ʹE | Luvisols & cambisols | 12 | 46.2 | 8.28 | 0.556 |
| dbh – diameter at breast height, h – height, BGB – dry biomass of coarse roots | |||||||
All study sites were located within a transition zone from the maritime to continental climate (Martyn 2000). The annual average temperatures are a little bit higher at Kampinoski National Park (KPN1 and KPN2) sites, where it amounts to 7–8 °C, whereas at Dobieszyn1, Dobieszyn2 and Kozienice sites it reaches 6–7 °C. January is the coldest month with average temperatures slightly below –2 °C all over central Poland. The highest temperature is recorded in July and ranges from 16–17 °C at southern sites (Dobieszyn1, Dobieszyn2, Kozienice) to 17–18 °C at northern ones (KPN1, KPN2). The investigated region has very poor precipitation and suffers from occasional droughts. The average annual rainfall rarely exceeds 550–600 mm. Soils that developed on glacio-fluvial melt water sands, glacial tills, clays as well as peats (KPN1 and KPN2 sites) are in general poor in nutrients and therefore not very fertile.
2.2 Biomass estimation
2.2.1 Fieldworks
At each of five locations we selected four stands of increasing ages assessed on the basis of tree-ring analyses. All of them grew on similar soils (Table 1). Furthermore, we randomly chose ten trees according to the diameter range in the stand so that all size classes were represented. The age of the selected trees varied from 1 to 16 years. The average diameter at the breast height (dbh) of the analysed birches ranged from 0.0 to 64.1 mm, whereas the height varied from 0.44 to 10.24 m (Table 1). These trees were dug out together with their root systems. The base level was marked at the bark prior to excavation to distinguish aboveground part of the tree from belowground one. We used pruning scissors and saws to divide each tree into the following components: stem, leaves, branches and roots. Root system was separated from the stem at the previously marked base level and thus included also the root crown (belowground part of a stump). Only coarse (i.e. d > 2 mm according to Snowdon et al. 2000) roots were collected. Soil and other organic materials were carefully cleared from the dug-out root systems with compressed air and brushes. All parts of the individual trees were weighed in the field using precise portable scales (accuracy of the most precise ones amounted to 0.01 g).
We took samples from each of the investigated components from every tree to determine the relationship between their fresh and dry biomass. In the laboratory, samples were oven-dried in 105 °C until they reached a constant weight and weighed to 0.01 g. The dry biomass of various components was calculated for each tree on the basis of corresponding fresh to dry mass ratios (Snowdon et al. 2000, 2002; Uri et al. 2007, 2012). Empirical material consisted of the data from 181 trees in total. As stated by Snowdon et al. (2002), this number is sufficient to determine reliable allometric equations.
2.2.2 Calculations
The direct measurement of the biomass of a tree and/or its components (usually expressed as dry weight of the stem, crown, stump or roots) is labour intensive, time-consuming and expensive, therefore allometric equations are developed to determine biomass as a function of easily measurable tree variables. This approach is based on the assumption that the above- and belowground development of the tree stays in an allometric balance (Drexhage and Colin 2002; Zianis et al. 2005; Muukkonen and Mäkipää 2006; Johansson 2007). Such formulae enable quick estimation of the biomass of subject components both in the scale of single trees and a whole stand.
To follow the above-mentioned concept we looked for the parameters of the model that would estimate the coarse roots biomass on the basis of dbh or/and the height of a tree. We assumed that such a relationship could be illustrated by one of the following formulae:
![]()
![]()
![]()
![]()
![]()
![]()

![]()
where BGB – belowground biomass of a single tree; a, b, c, e – equation parameters; d – tree diameter at breast height; h – tree height.
Majority of selected forms of the allometric equations is widely used in biomass estimation as reviewed by Zianis et al. (2005), Muukkonen and Mäkipää (2006) and Repola et al. (2007). One can also find models that use log-transformation of both the belowground biomass and the independent variables. Such formulae were elaborated for birch by Santantonio et al. (1977) and Mälkönen (1977). We decided however, not to use this type of model as a reverse transformation of the obtained equation in order to directly calculate the value of dependent variables instead of its logarithm, results in a biased estimation of it (Meyer 1944).
We estimated the parameters of the Eqs. 1–8 and compared them with the use of the widely recognised measures of model’s goodness-of-fit, i.e.: root mean square error (RMSE), mean square error (MSE) and coefficient of determination (R2). Additionally, to find out the most accurate one, we analysed the distribution of percentage errors (PE) of elaborated equations. PE [%] for individual equations were calculated according to the following formula:

where BGBeq – belowground biomass estimated with a given equation; BGBr – observed biomass.
We analysed the influence of tree’s size and age on the amount of accumulated belowground biomass. For those relationships that were of a non-linear character, the coefficient of determination (R2) was used to describe their strength.
Allocation of the biomass within a tree can be described by the means of R/S (root-to-shoot) ratio that expresses the belowground biomass as a fraction of the aboveground one (Mokany et al. 2006). We calculated R/S values for each of the analysed sample trees. To recognize how the portion of biomass that a plant invests in its stability as well as nutrient uptake changes with the increase of its size and over time, we correlated the calculated R/S values with the age, aboveground biomass, dbh as well as height of analysed birches. Similarly with the bulk belowground biomass, these relationships turned on to have a non-linear character and we used R2 to assess their strength.
3 Results
Root systems of the analysed young birches constituted mainly of roots with lateral and lateral-sinker types and had a rather flat, but spread out architecture. Coarse roots biomass of the investigated trees ranged from 0.7 to 4305.5 g/tree (422.6 g/tree on average) showing great variability (standard deviation = 783 g/tree) and asymmetry of distribution (Table 2). It stayed in a close-to-linear relationship with the aboveground biomass of these trees (r = 0.979; p < 0.01). A clear dependence of this attribute based on the age and size of a tree was found (Fig. 1). The younger or smaller the tree, the less, in terms of weight, coarse roots it had (r = 0.679, 0.799 and 0.854 for age, height and dbh, respectively). The variability of the estimated biomass also depended on the age and size of the trees (Fig. 1). This relationship however seems to be more evident in the case of age.
| Table 2. Basic descriptive statistics of coarse roots biomass (BGB) and root-to-shoot (R/S) ratio for analysed young birches growing on post-agricultural lands in central Poland (n = 181). | ||||||
| min | m | me | max | sd | cv | |
| BGB [kg/tree] | 0.0007 | 0.4226 | 0.1234 | 4.3055 | 0.7829 | 185 |
| R/S | 0.091 | 0.245 | 0.193 | 1.015 | 0.154 | 63 |
| min – minimum, m – mean, me – median, max – maximum, sd – standard deviation, cv – coefficient of variation [%]. | ||||||
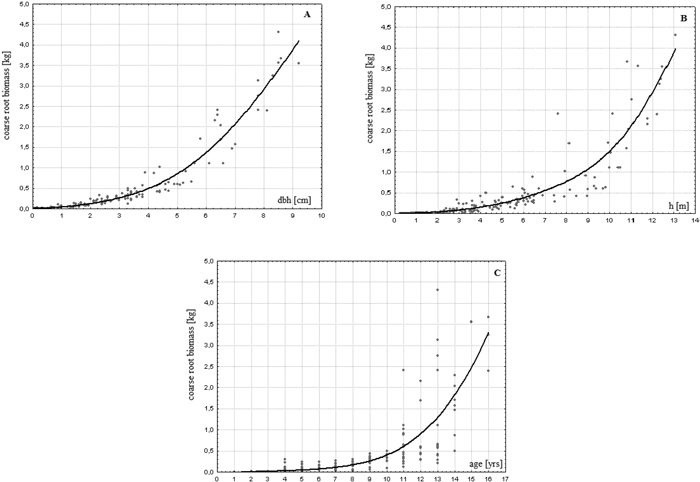
Fig. 1. Relationship between coarse root biomass and dbh (A), height (B) and age (C) of a tree in young successional silver birch stands on post-agricultural lands in central Poland
In general, all the applied allometric equations fit the empirical data well, which is confirmed by the high values of the coefficient of determination (Table 3). Only estimates from Eq. 3 seemed to be less reliable than those obtained from other formulae. This model related to the highest RMSE value as well. It was also noted that in the case of all equations MSE values did not deviate significantly from 0(p < 0.01). Percentage error analysis revealed a greater diversification among analysed formulae. Eq. 7 turned out to be the most accurate, with the lowest PE value (4% for the whole material, –6% after the trees with no dbh were excluded from the analysis). This formula, however, characterises with very high coefficient of variation, which is probably due to the splining of two different functions within one model. The exclusion of trees with dbh = 0from PE analysis gives similar results although in general error values are smaller (Table 3). Additionally, PE given for Eq. 7 shows no age-dependency (r = 0.08; p < 0.01), whilst this is not the case for other formulae. Finally, allometric equations for the assessment of coarse root biomass of young birches growing on the post-agricultural lands takes the following form:
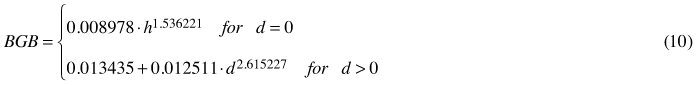
where BGB – belowground biomass of a single tree [kg]; d – tree diameter at breast height [cm]; h – tree height [m].
| Table 3. Goodness-of-fit measures for analysed allometric equations. | |||||||||
| Eq. | R2 | RMSE | MSE | m PEall | sd PEall | cv PEall | m PEnd0 | sd PEnd0 | cv PEnd0 |
| 1 | 0.943 | 0.188 | 0.002 | 202 | 546 | 270 | 31 | 267 | 854 |
| 2 | 0.943 | 0.189 | 0.016 | –40 | 50 | 123 | –22 | 43 | 191 |
| 3 | 0.849 | 0.308 | 0.039 | –39 | 56 | 141 | –23 | 54 | 231 |
| 4 | 0.938 | 0.197 | 0.024 | –44 | 49 | 113 | –27 | 44 | 164 |
| 5 | 0.939 | 0.195 | 0.002 | 321 | 833 | 259 | 54 | 406 | 751 |
| 6 | 0.929 | 0.211 | 0.002 | 390 | 997 | 256 | 68 | 486 | 715 |
| 7 | 0.943 | 0.189 | 0.011 | 4 | 52 | 1201 | –6 | 35 | 558 |
| 8 | 0.943 | 0.188 | 0.001 | 108 | 247 | 229 | 23 | 109 | 466 |
| Eq. – number of analysed equation, R2 – coefficient of determination, RMSE – root mean square error, MSE – mean square error, PEall – whole range of dbh included in percent error calculation, PEnd0 – only trees with dbh > 0 included in percent error calculation; m – mean, sd – standard deviation, cv – coefficient of variation [%]. | |||||||||
On average, the analysed birches allocated to the roots biomass an amount which equalled almost 25% of the aboveground amounts (Table 2). The share of the belowground biomass in relation to aboveground part of the plant varied from 10 to 100% indicating that some of the trees (especially younger ones) developed root systems that weighed as much as the stems and foliage together. We found an evident tendency of a decrease in the share of roots in the aboveground biomass of the analysed trees with increasing age (r = –0.613, p < 0.01), dbh (r = –0.545, p < 0.01) and height (r = –0.582, p < 0.01). One can observe stabilisation of the R/S ratio at level of ca. 0.17 at certain values of these parameters. The variability of R/S values is strongly reduced for dbh > 4 cm or for h > 6.5 m (Fig. 2). The relationship with age is of a more sophisticated character.
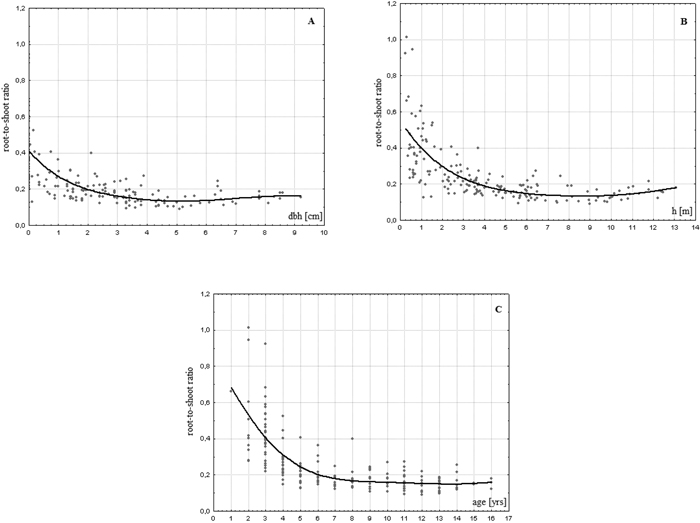
Fig. 2. Relationship between R/S ratio values and dbh (A), height (B) and age (C) of a tree in young successional silver birch stands on post-agricultural lands in central Poland.
4 Discussion
Belowground part of the forest ecosystem is estimated to sequester ca. 50% of carbon annually accumulated by terrestrial plants (Waisel et al. 1991; Vogt et al. 1996; Lorenz and Lal 2010). Despite the significant impact of belowground pools in the carbon budget, studies on quantification and its role are rather rare (Mokany et al. 2006; Lorenz and Lal 2010; Tyrrell et al. 2012). Available allometric models usually omit biomass of that part of plants or substitute information about it with a value calculated based on very general ratio suggested by e.g. IPCC. Such situations undoubtedly result from the fact that the determination of root and soil biomass is very laborious and expensive (Snowdon et al. 2000). The elaboration of allometric equations to model belowground biomass based on measurements of parameters of aboveground parts of trees has recently gained wider interest, thus more and more formulae are presented (e.g. Petersson and Ståhl 2006; Johansson 2007; Repola et al. 2007; Uri et al. 2007; Repola 2008; Varik et al. 2013 for birch).
Studies on root system biomass suffer from a lack of clear definition that can allow distinguishing different root fractions. The literature review provides various threshold values. The most widely used division into fine and coarse roots, sets the diameter usually at 2 mm (Gifford 2000; Retzlaff et al. 2001; Mund et al. 2002; Snowdon et al. 2002). Further delimitation into coarse root fractions is based on the diameter that varies from 5 to 300 mm. In addition to this, some authors distinguish root crown as a separate part of the upper part of the root system (e.g. Snowdon et al. 2002). Another important issue is that various authors quite arbitrarily include individual fractions in the total root biomass determination. Fine roots are the most frequently omitted and are either not included in biomass calculation at all, or are assigned to the soil pool. The omission of some parts of root biomass (especially fine roots) causes an underestimation of the total belowground biomass of up to 10% (Mund et al. 2002). The estimation of different fractions of roots requires different methods, which are hard to combine at one time of fieldworks. Coarse roots need to be excavated as a whole, while fine roots require also a proper sampling scheme and the use of e.g. soil corers (e.g. Snowdon et al. 2000, 2002).
Allometric models available for silver birch usually omit belowground biomass or substitute it with either a general ratio (IPCC 2006) or with values/equations elaborated for other species (Marklund 1988). Our results fill the gap in that field, allowing to estimate the belowground biomass pool for birch stands growing on post-agricultural lands as such works have previously been rather limited (Petersson and Ståhl 2006; Johansson 2007; Repola et al. 2007; Uri et al. 2007; Repola 2008). Almost all the tested models estimated coarse root biomass well. We chose the equation of spline type (Eq. 7) as it fits the empirical data the best. Since very young trees don’t have dbh, the model has to be based on another easily measurable variable to provide sufficient estimation of belowground biomass. Basing the estimation of the biomass of the smallest trees on their height meets that demand and the equation manages to cover the whole range of analysed trees sizes.
The estimation of belowground biomass with the proposed equation cannot be directly compared to the results from the application of functions elaborated on by other authors (e.g. Petersson and Ståhl 2006; Johansson 2007; Uri et al. 2007; Repola 2008). This is because a number of sample trees and the range of their dimensions vary greatly among the studies. In our study root biomass was determined based on the data from 181 trees. Meanwhile, Repola (2008) used 39, Petersson and Ståhl (2006) – 13 and Uri et al. (2007) – only 5 model trees. Johnsson (2007) analysed four different spacings at two various soil types and each such combination was represented by ca. 80 trees. According to Snowdon et al. (2002) reliable allometric equations can be elaborated on sample material consisting of more than 20 trees. Repola (2008) applied roots of minimum diameter up to 10 mm, while Petersson and Ståhl (2006) included stumps and roots to a diameter of 5 mm. Johnsson (2007) investigated roots with diameter >1 mm. Our equation utilizes also trees that haven’t reached breast height. Coverage of the range of variables used in the determination of biomass equations is crucial in terms of their comparison. As shown by Bijak and Zasada (2007), who applied nine various functions from the literature for estimation of belowground biomass of Scots pine stands, results can vary significantly regarding the formulae. Wang et al. (2002) found large discrepancies between measured data and estimates based on the previously published equations. They suggest careful checks of the equations taken from the literature for their applicability in local conditions. Similar recommendations were discussed by Mokany et al. (2006) regarding the use of R/S ratio values.
Belowground parts of the investigated young birches were constituted mainly of lateral and lateral-sinker roots and had rather a flat, spreading out character. This stays in accordance to findings of Köstler et al. (1968) who stated that birch trees develop typically a heart root system. Kalliokoski et al. (2008) observed similar pattern for birches in southern Finland, especially on poorer soils, and suggested that soil conditions are crucial factor affecting roots architecture. On the contrary, our results are opposite to the findings from young birch stands in Sweden (Johansson 2007) and Estonia (Uri et al. 2007; Varik et al. 2013). Diverse soil conditions might have significantly influenced the opposite type of the root systems development. The biomass of analysed coarse roots however, was similar to reported by other authors for birches of the same age (Johansson 2007; Uri et al. 2007; Varik et al. 2013). It also turned out to be highly dependent on the size and age of trees. This finding is consistent with previous reports for silver birch (Johansson 2007; Uri et al. 2007) and various other species. Such patterns were observed for example with Scots pine (Makkonen and Helmisaari 1999; Bijak and Zasada 2007; Jagodziński and Kałucka 2010), Norway spruce (Mund et al. 2002; Vesterdal et al. 2007; Børja et al. 2008), beech (Huet et al. 2004; Claus and George 2005; Genet et al. 2010) and oak (Claus and George 2005; Vesterdal et al. 2007; Genet et al. 2010).
Biomass allocation within a tree changes over time. Increasingly larger amount of biomass and carbon are allocated in the stems as trees get older (Mund et al. 2002; Law et al. 2003; Peichl and Arain 2006). We also found evidence of a tendency for a decrease in the share of root biomass in relation to the aboveground biomass of the analysed birches with the increasing age and size of a tree. Seedlings store relatively more biomass and carbon in roots than trees in the poles and old growth stand development stages do. This is because at the first stage of development it is more crucial for the plant to produce a sufficiently spread out root system than to invest in stem growth. It gives a greater possibility for the effective uptake of nutrients by fine roots. Competition among specimens in young stands characterised with high stocking is great and one can observe specific ‘investment’ in belowground biomass that provides plants with water and nutrients (Casper and Jansen 1997; Jagodziński and Oleksyn 2009). Variability of R/S values is also an effect of root system architecture as well as dimensions of aboveground part of a tree. Other features that influence biomass of the roots include environmental conditions such as soil texture, soil fertility and site properties as well as climate (Jackson et al. 1996; Cairns et al. 1997; Snowdon et al. 2000; Brown 2002; Mokany et al. 2006; Tyrrell et al. 2012).
Mokany et al. (2006) found that the use of R/S ratios instead of allometric equations based on aboveground biomass was, in general, a more accurate method for predicting root biomass. For calculating the belowground biomass IPCC (2006) recommends the application of a single R/S value dependent only on tree type (coniferous or deciduous) and vegetation zone. Mokany et al. (2006) suggest a more diversified protocol, in which this factor is based on vegetation type and the amount of aboveground biomass. Although dimensions and volume (thus biomass) of aboveground parts of trees is directly related to their age, it is advisable, as the presented study shows, to include the age of a specimen into the determination of belowground biomass as well, especially when the investigation deals with very young trees. Straightforward implementation of IPCC recommendations may lead to biased estimation of the biomass.
5 Conclusions
The elaborated coarse root biomass equation for individual silver birch trees can be applicable to young (up to 15 years of age) Betula spp. stands as it is based on variables commonly measured in forest inventories and is formulated so that biomass estimation covers the widest possible range of the dbh and height values. Although the equation was determined using data from subjectively selected sample plots, they represent typical conditions for the majority of post-agricultural lands in central Poland and hence its applicability should be considered.
Age and size of the trees are the most important factors that influence the amount of belowground biomass and its allocation to coarse roots in cases of the analysed birches. This observation is consistent with current knowledge about the distribution of biomass in forest tree species. High dependency of the observed R/S ratio values on the tree’s age however, suggest that this feature should be included in determination of belowground biomass, especially where very young specimens are concerned.
Acknowledgements
The research was supported by grant N N305 400238 ‘Ecological consequences of the silver birch (Betula pendula Roth) secondary succession on abandoned farmlands in central Poland’ from the Polish National Science Center. We thank two anonymous reviewers for their comments that allowed to improve the manuscript.
References
Bijak Sz., Zasada M. (2007). Oszacowanie biomasy korzeni w drzewostanach sosnowych Borów Lubuskich. [Assessment of the belowground biomass in Scots pine stands of Bory Lubuskie]. Sylwan 151(12): 21–29. [In Polish with English abstract and summary].
Børja I., De Witt H.A., Steffenrem A., Majdi H. (2008). Stand age and fine root biomass, distribution and morphology in a Norway spruce chronosequence in southeast Norway. Tree Physiology 28: 773–784. doi:10.1093/treephys/28.5.773.
Brown S. (2002). Measuring carbon in forests: current status and future challenge. Environmental Pollution 116: 363–372.
Cairns M., Brown S., Helmer E., Baumgardner M. (1997). Root biomass allocation in the world’s upland forests. Oecologia 111: 1–11.
Carroll M., Milakovsky B., Finkral A., Evans A., Ashton M.S. (2012). Managing carbon sequestration and storage in temperate and boreal forests. In: Ashton M.S., Tyrrell M.L., Spalding D., Gentry B. (eds.). Managing forest carbon in a changing climate. Springer, Dordrecht, Heidelberg, London, New York. p. 205–226. doi:10.1007/978-94-007-2232-3_5.
Casper B.B., Jackson R.B. (1997). Plant competition underground. Annual Review of Ecology and Systematics 28: 545–570.
Central Statistical Office (2011). Leśnictwo. [Forestry yearbook]. Central Statistical Office, Warszawa. 312 p. [In Polish].
Claesson S., Sahlén K., Lundmark T. (2001). Functions for biomass estimation of young Pinus sylvestris, Picea abies and Betula spp. from stands in northern Sweden with high stand densities. Scandinavian Journal of Forest Research 16: 138–146.
Claus A., George E. (2005). Effect of stand age on fine-root biomass and biomass distribution in three European forest chronosequences. Canadian Journal of Forest Research 35(7): 1617–1625. doi:10.1139/x05-079.
Drexhage M., Colin F. (2002). Estimating root system biomass from breast-height diameter. Forestry 74: 491–497.
Genet H., Bréda N., Dufrêne E. (2010). Age-related variation in carbon allocation at tree and stand scales in beech (Fagus sylvatica L.) and sessile oak (Quercus petraea (Matt.) Liebl.) using a chronosequence approach. Tree Physiology 30(2): 177–192. doi:10.1093/treephys/tpp105.
Gifford R. (2000). Carbon content of woody roots. NCAS Technical Report 7. 16 p.
Gower S.T. (2003). Patterns and mechanisms of the forest carbon cycle. Annual Review of Environment and Resources 28: 169–204. doi:10.1146/annurev.energy.28.050302.105515.
Guo L.B., Gifford R.M. (2002). Soil carbon stocks and land use change: a meta analysis. Global Change Biology 8: 345–360. doi:10.1046/j.1354-1013.2002.00486.x.
Hodgman T., Munger J., Hall J.S., Ashton M.S. (2012). Managing afforestation and reforestation for carbon sequestration: considerations for land managers and policy makers. In: Ashton M.S., Tyrrell M.L., Spalding D., Gentry B. (eds.). Managing forest carbon in a changing climate. Springer, Dordrecht, Heidelberg, London, New York. p. 227–256. doi:10.1007/978-94-007-2232-3_5.
Huet S., Forgeard F., Nys C. (2004). Above- and belowground distribution of dry matter and carbon biomass of Atlantic beech (Fagus sylvatica L.) in a time sequence. Annals of Forest Science 61(7): 683–694. doi:10.1051/forest:2004063.
Hynynen J., Niemistö P., Viherä-Aarnio A., Brunner A., Hein S., Velling P. (2010). Silviculture of birch (Betula pendula Roth and Betula pubescens Ehrh.) in northern Europe. Forestry 83(1): 103–119.
Hytönen J., Aro L. (2012). Biomass and nutrition of naturally regenerated and coppiced birch on cutaway peatland during 37 years. Silva Fennica 46(3): 377–394.
IPCC (2006). IPCC guidelines for national greenhouse gas inventories. Vol. 4. Agriculture, forestry and other land use. IPCC. ISBN 4-88788-032-4.
Jackson R.B., Candell J., Ehleringer J., Mooney H., Sala O., Schulze E. (1996). A global analysis of root distributions for terrestrial biomes. Oecologia 108: 389–411.
Jagodziński A.M., Kałucka I. (2010). Fine roots biomass and morphology in a chronosequence of young Pinus sylvestris stands growing on a reclaimed lignite mine spoil heap. Dendrobiology 64: 19–30.
Jagodziński A.M., Oleksyn J. (2009). Ekologiczne konsekwencje hodowli drzew w różnym zagęszczeniu. II. Produkcja i alokacja biomasy, retencja biogenów. [Ecological consequences of silviculture at variable stand densities II. Biomass production and allocation, nutrient retention]. Sylwan 153(3): 147–157. [In Polish with English abstract and summary].
Johansson T. (1999). Biomass equations for determining functions of pendula and pubescent birches growing on abandoned farmland and some practical implications. Biomass and Bioenergy 16: 223–238.
Johansson T. (2007). Biomass production and allometric above- and below-ground relations for young birch stands planted at four spacings on abandoned farmland. Forestry 80(1): 41–52. doi:10.1093/forestry/cpl049.
Kalliokoski T., Nygren P., Sievänen R. (2008). Coarse root architecture of three boreal tree species growing in mixed stands. Silva Fennica 42(2): 189–210.
Karlsson A., Albrektson A., Forsgren A., Svensson L. (1998). An analysis of successful natural regeneration of downy and silver birch on abandoned farmland in Sweden. Silva Fennica 32(3): 229–240.
Köstler J.N., Brückner E., Bibelriether H. (1968). Die Wurzeln der Waldbäume. Paul Parey Publishers, Hamburg–Berlin. [In German].
Kuznetsova T., Lukjanova A., Mandre M., Lõhmus K. (2011). Aboveground biomass and nutrient accumulation dynamics in young black alder, silver birch and Scots pine plantations on reclaimed oil shale mining areas in Estonia. Forest Ecology and Management 262(2): 56–64. doi:10.1016/j.foreco.2010.09.030.
Law B.E., Sun O.J., Campbell J., van Tuyl S., Thornton P.E. (2003). Changes in carbon storage and fluxes in a chronosequence of ponderosa pine. Clobal Change Biology 9(4): 510–524. doi:10.1046/j.1365-2486.2003.00624.x.
Lorenz K., Lal R. (2010). Carbon sequestration in forest ecosystems. Springer, Dordrecht, Heidelberg, London, New York. 288 p.
Makkonen K., Helmisaari H-S. (2001). Fine root biomass and production in Scots pine stands in relation to stand age. Tree Physiology 21: 193–198.
Mälkönen E. (1977). Annual primary production and nutrient cycle in birch stand. Communicationes Instituti Forestalis Fenniae 91(5). 35 p.
Marklund G. (1988). Biomass functions for pine, spruce and birch in Sweden. Swedish University of Agricultural Sciences, Department of Forest Survey, Report 45. 71 p.
Martyn D. (2000). Klimaty kuli ziemskiej. [Climates of the Earth]. PWN, Warszawa. 360 p.
Meyer H.A. (1944). A correction for systematic error occurring in the application of the logarithmic volume equation. Pennsylvania State University, Forest Research Paper 7.
Mokany K., Raison R., Prokushkin A. (2006). Critical analysis of root:shoot ratios in terrestrial biomes. Global Change Biology 12: 84–96.
Mund M., Kummetz E., Hein., Baier G., Schulze E. (2002). Growth and carbon stocks of spruce forest chronosequence in central Europe. Forest Ecology and Management 171: 275–296.
Muukkonen P., Mäkipää R. (2006). Biomass equations for European trees: addendum. Silva Fennica 40(4): 763–773.
Peichl M., Arain A. (2006). Above- and belowground ecosystem biomass and carbon pools in an age-sequence of temperate pine plantation forests. Agricultural and Forest Meteorology 140: 51–63.
Petersson H., Ståhl G. (2006). Functions for below-ground biomass of Pinus sylvestris, Picea abies, Betula pendula and Betula pubescens in Sweden. Scandinavian Journal of Forest Research 21(7): 84–93.
Repola J. (2008). Biomass equations for birch in Finland. Silva Fennica 42(4): 605–624.
Repola J., Ojansuu R., Kukkola M. (2007). Biomass functions for Scots pine, Norway spruce and birch inFinland. Working Papers of the Finnish Forest Research Institute 53. 28 p.
Retzlaff W., Handest J., O’Malley D., McKeand S., Topa M. (2001). Whole-tree biomass and carbon allocation of juvenile trees of loblolly pine (Pinus taeda): influence of genetics and fertilization. Canadian Journal of Forest Research 31: 960–970.
Santantonio D., Hermann R.K., Overton W.S. (1977). Root biomass studies in forest ecosystems. Pedobiologia 17: 1–31.
Snowdon P., Eamus D., Gibbons P., Khanna P., Keith H., Raison. J., Kirschbaum M. (2000). Synthesis of allometrics. Review of root biomass and design of future woody biomass sampling strategies, NCAS Technical Report 17. 113 p.
Snowdon P., Raison. J., Keith H., Ritson P., Grierson P., Adams M., Montagu K., Hiu-Quan B., Burrows W., Eamus D. (2002). Protocol for sampling tree and stand biomass. NCAS Technical Report 31. 66 p.
Spalding D., Kendrili E., Oliver Ch.D. (2012). The role of forests in global carbon budgeting. In: Ashton M.S., Tyrrell M.L., Spalding D., Gentry B. (eds.). Managing forest carbon in a changing climate. Springer, Dordrecht, Heidelberg, London, New York. p. 165–179. doi:10.1007/978-94-007-2232-3_5.
Tahvanainen T., Forss E. (2008). Individual tree models for the crown biomass distribution of Scots pine, Norway spruce and birch in Finland. Forest Ecology and Management 255: 455–467.
Tyrrell M.L., Ross J., Kelty M. (2012). Carbon dynamics in the temperate forest. In: Ashton M.S., Tyrrell M.L., Spalding D., Gentry B. (eds.). Managing forest carbon in a changing climate. Springer, Dordrecht, Heidelberg, London, New York. p. 77–108. doi:10.1007/978-94-007-2232-3_5.
Uri V., Lõhmus K., Ostonen I., Tullus H., Lastik R., Vildo M. (2007). Biomass production, foliar and root characteristics and nutrient accumulation in young silver birch (Betula pendula Roth.) stand growing on abandoned agricultural land. European Journal of Forest Research 126(4): 495–506. doi:10.1007/s10342-007-0171-9.
Uri V., Varik M., Aosaar J., Kanal A., Kukumägi M., Lõhmus K. (2012). Biomass production and carbon sequestration in a fertile silver birch (Betula pendula Roth) forest chronosequence. Forest Ecology and Management 267: 117–126. doi:10.1016/j.foreco.2011.11.033.
Varik M., Aosaar J., Ostonen I., Lõhmus K., Uri V. (2013). Carbon and nitrogen accumulation in belowground tree biomass in a chronosequence of silver birch stands. Forest Ecology and Management 302: 62–70. doi:10.1016/j.foreco.2013.03.033.
Vesterdal L., Rosenqvist L., van der Salm C., Hansen K.,Groenenberg B.J., Johansson M.B. (2007). Carbon sequestration in soil and biomass following afforestation: experiences from oak and Norway spruce chronosequences in Denmark, Sweden and the Netherlands. In: Heil G., Muys B., Hansen K. (eds.). Environmental effects of afforestation in north-western Europe – from field observations to decision support. Plant and Vegetation 1: 19–52.
Vogt K.A., Vogt D.J., Palmiotto P.A., Boon P., O’Hara J., Asbjornsen H. (1996). Review of root dynamics in forest ecosystems grouped by climate, climatic forest type and species. Plant Soil 187: 159–219.
Waisel Y., Eshel A., Kafkafi U. (1991). Plant roots. The hidden half. Marcel Dekker, Inc., New York. 948 p.
Wang J.R., Zhong A.L., Kimmins J.P. (2002). Biomass estimation errors associated with the use of published regression equations of paper birch and trembling aspen. Northern Journal of Applied Forestry 19(3): 128–136.
Zając S., Gil W. (eds.). (2003). Zalesienia w Europie – doświadczenia i zamierzenia. [Afforestation in Europe – experiences and prospects]. Instytut Badawczy Leśnictwa, Warszawa. 282 p. ISBN 83-87647-33-0.
Zianis D., Muukkonen P., Mäkipää R., Mencuccini M. (2005). Biomass and stem volume equations for tree species in Europe. Silva Fennica Monographs 4. 63 p.
Total of 58 references

