Search reversion within s-metaheuristics: impacts illustrated with a forest planning problem
Bettinger P., Demirci M., Boston K. (2015). Search reversion within s-metaheuristics: impacts illustrated with a forest planning problem. Silva Fennica vol. 49 no. 2 article id 1232. https://doi.org/10.14214/sf.1232
Highlights
- The interruption of the sequence of events used to explore a solution space and develop a forest plan, and the re-initiation of the search process from a high-quality, known starting point (reversion) seems necessary for some s-metaheuristics
- When using a s-metaheuristic, higher quality forest plans may be developed when the reversion interval is around six iterations of the model.
Abstract
The use of a reversion technique during the search process of s-metaheuristics has received little attention with respect to forest management and planning problems. Reversion involves the interruption of the sequence of events that are used to explore the solution space and the re-initiation of the search process from a high-quality, known starting point. We explored four reversion rates when applied to three different types of s-metaheuristics that have previously shown promise for the forest planning problem explored, threshold accepting, tabu search, and the raindrop method. For two of the s-metaheuristics, we also explored three types of decision choices, a change to the harvest timing of a single management unit (1-opt move), the swapping of two management unit’s harvest timing (2-opt moves), and the swapping of three management unit’s harvest timing (3-opt moves). One hundred independent forest plans were developed for each of the metaheuristic / reversion rate combinations, all beginning with randomly-generated feasible starting solutions. We found that (a) reversion does improve the quality of the solutions generated, and (b) the rate of reversion is an important factor that can affect solution quality.
Keywords
forest planning;
heuristics;
threshold accepting;
tabu search;
spatial harvest scheduling;
adjacency constraints;
mixed integer goal programming
-
Bettinger,
School of Forestry and Natural Resources, 180 E. Green Street, University of Georgia, Athens, Georgia, USA 30602
E-mail
pbettinger@warnell.uga.edu

- Demirci, General Directorate of Forestry, Ministry of Forest and Water Affairs, Republic of Turkey E-mail mehmetdemirci@yahoo.com
- Boston, Department of Forest Engineering, Resources and Management, College of Forestry, Oregon State University, USA E-mail Kevin.Boston@oregonstate.edu
Received 8 August 2014 Accepted 21 October 2014 Published 12 March 2015
Views 177430
Available at https://doi.org/10.14214/sf.1232 | Download PDF

1 Introduction
Forests, one of nature’s most bountiful and versatile renewable resources, provide social, cultural, environmental, and economic benefits and services to human society. Forest managers often need to balance the functions that forests serve, since demands of society for forest products and other provisional services may at times seem to be more immediate and important than cultural, regulating, or supporting services. Forest management plans are often developed as tools to promote transparency of management with the intent that they can be used to help manage conflicts between user groups and guide the timing and placement of management activities. Land use planning regulations in the United States (36 C.F.R. 219.4), for example, require the U.S. Forest Service to develop strategic management alternatives during the planning process with the participation of user groups. Private forest owners (companies and individuals) also often desire to examine management alternatives for their forests. In terms of the methods used to help develop these plans, they range from ad-hoc unstructured analyses of specific alternatives to the formulation and development of mathematical problems, solved often with linear or mixed integer programming algorithms and increasingly with heuristics. Constraints that are based on spatial rules are now often important for long-term planning (Borges et al. 2014b). As a consequence, many plans today include non-linear spatial relationships (e.g., Boston and Bettinger 2006).
Forest managers often require integer solutions (yes-no or 0–1 decisions) with regard to the potential harvest of forest stands or the development of other resources, such as roads. Two general methodologies, exact and heuristic, describe the approaches people have used to solve these problems (Crowe and Nelson 2003). Exact methods applied to forest-level harvest scheduling problems include linear programming (e.g., Borges et al. 2014a), mixed integer programming (e.g., Tóth et al. 2012), goal programming (e.g., Limaei et al. 2014), non-linear programming (e.g., Härtl et al. 2013) and dynamic programming (e.g., Wei and Hoganson 2008). Linear programming has been used extensively for forest-level strategic and tactical planning in North America (Bettinger and Chung 2004), and mixed integer programming is often used when harvest adjacency constraints are considered. Linear programming approaches optimize an objective function subject to inequality or equality constraints which define a convex polyhedral set, and the optimal solution is located using the maximum principle for convex functions. The Simplex Method and decomposition approaches represent processes for transforming the matrix of coefficients so that a mathematically optimal solution can be identified (Liittschwager and Tcheng 1967). When necessary global optimality or sufficient global optimality conditions exist, global optimality can also be guaranteed when using non-linear programming methods (Li and Wang 2014).
Mixed-integer programming approaches often use branch and bound algorithms to solve discrete or combinatorial problems. Branch and bound algorithms systematically explore alternative solutions to a problem by computing lower and upper bounds on potential subsets of the problem (branches) and deciding, based on these values, to either prune (disregard) the branch or explore further alterations of the subset. The process continues until the set of subproblems has been completely explored, when the lower and upper bounds to the problem are equal, or when the gap between them is less than some tolerance value (McDill and Braze 2001). Goal programming is very similar to linear programming, and involves the use of two or more different metrics (usually defined as goals, or as deviations from goals) within the objective function. Each goal is potentially weighted to emphasize the importance of the goals or to standardize the outcome values. Dynamic programming divides a problem into subproblems, each of which are solved and combined, with the goal of reducing the computational burden. Dynamic programming relies on the Principle of Optimality or a contiguity condition (when the Principle is not valid) to warrant that the solution generated is optimal (Galperin 2006). The advantage of these exact approaches is that optimality is generally guaranteed (Nelson 2003), to the extent of the optimality tolerance and other parameters used within the solver that are employed (McDill and Braze 2001). The main disadvantage of some of these approaches is associated with the time required to generate the optimal solution, typically when integer decision variables are required (Fischer et al. 2014).
Heuristic procedures in general are not necessarily new, and they do not guarantee that an optimal solution will be obtained, yet they have been designed to locate sub-optimal solutions to a problem when the time or cost of locating the optimal solution is of concern (Hillier and Lieberman 1980). Over the last two decades, the value of using metaheuristics such as simulated annealing (e.g., Falcão and Borges 2002; Borges et al. 2014b), tabu search, and genetic algorithms (e.g., Falcão and Borges 2001) in forest planning has been demonstrated. For example, Bettinger et al. (1997) developed a tabu search algorithm to demonstrate how two goals from a U.S. Forest Service strategic plan, involving commodity production and wildlife habitat, could be simultaneously addressed. Brumelle et al. (1998) developed a tabu search algorithm to address multi-criteria forest optimization problems that involved the timing and placement of harvest activities, and Bettinger et al. (1998) presented a land management scheduling model based on tabu search for scheduling timber harvests in order to meet aquatic habitat quality and commodity production goals. Many other applications of metaheuristics to forest management issues have been explored. As examples, Seo et al. (2005) presented an approach to locate near-optimal silvicultural development paths for Norway spruce (Picea abies) stands using simulated annealing. Bettinger et al. (2007) developed a tabu search model to select management actions for individual forest stands to both improve forest health and to meet a higher-level landscape objectives. Heinonen et al. (2011) developed a simulated annealing model to assess wind risk and potential wind-related damage, and used this information to inform the development of forest plans.
Most of the early literature involving forest management problems has consisted of s-metaheuristics operating in 1-opt mode, where the status of a single management unit (stand or road) is changed and the solution is re-evaluated. Bettinger et al. (1999, 2002), Caro et al. (2003), and Heinonen and Pukkala (2004) illustrated how 2-opt (or more) moves (the swapping of management action assignments between two management units) can be used to intensify a search within high-quality areas of a solution space and thus produce higher-valued solutions as compared to the use of 1-opt moves alone. These efforts involved tabu search, which proved computationally expensive for each move in the search process, since the 2-opt neighborhoods were much larger than the associated 1-opt neighborhoods (when all neighboring solutions are included in the assessment); yet, the quality of the solutions improved. However, there are ways in which neighborhood assessments within tabu search can be implemented in a more efficient manner, for example by sampling from a smaller set of the total potential moves from the neighborhood or by partitioning the neighborhood and only assessing a small deterministic block of potential moves in a region-limited manner (e.g., as in Bettinger et al. 2007).
The process of reversion within metaheuristics is not a new idea, yet has received relatively little attention in the literature. The goal of reversion is to intensify the search for the optimal solution to a problem around known high-quality local optima. The assumption is that better solutions can be found in this same neighborhood. The process of re-starting a search process from a saved local optimum is alluded to in Talbi (2009) in the description of a variable neighborhood descent algorithm. Randomization approaches (Glover and Laguna 1993, 1997), the identification of critical events within the search process, and parallel processing procedures (Glover and Laguna 1997) have been suggested as ways of accomplishing this within tabu search. In an improvement phase of an airline scheduling algorithm (Sinclair et al. 2014), reversion to the best solution stored in memory is embedded in a shortest-path heuristic process. In a reassignment phase of a clustering algorithm (Sağlam et al. 2006), reversion to a relaxed mixed-integer solution is embedded within a heuristic process. In other search processes, the chain of events in transforming one solution to another may technically very often revert to the best solution stored in memory, particularly when the probability of acceptance of inferior solutions decreases with search time and the search is designed to revert to the best solution (Cordeau and Maischberger 2012; Matusiak et al. 2014). However, this is not the standard case in some s-metaheuristics such as tabu search. Further, in some search processes that resemble Markov chains (e.g., threshold accepting), the typical transformation process for creating solution j from solution i does not include a phase for re-starting the process or reverting to the best solution.
Comparisons of heuristic methods for application in forest management problems have been described in the literature as well. Boston and Bettinger (1999) compared the performance of three metaheuristic techniques that were commonly used to solve spatial harvest scheduling problems: Monte Carlo integer programming, simulated annealing, and tabu search. Borges et al. (1999) compared the performance of a decomposition strategy inside dynamic programming to random search and to a heuristic that ranks potential choices for inclusion into the solution. Falcão and Borges (2002) compared the performance of three types of heuristics: simulated annealing, an evolution program, and a sequential quenching and tempering model to a problem with open size constraints and old forest patch requirements. Bettinger et al. (2002) compared the performance of eight types of metaheuristic techniques when applied to three increasingly difficult forest planning problems that had commodity production and wildlife habitat goals. Heinonen and Pukkala (2004) compared the performance of four metaheuristic techniques, random ascent, Hero, simulated annealing, and tabu search, when applied to a forest planning problem with a spatial objective. Zhu and Bettinger (2008a) developed three metaheuristics (threshold accepting, tabu search, and a combined heuristic) to assess the quality of forest plans and the time required to develop them. Each of these efforts provided interesting results that suggested modifications to the intensification and diversification aspects of a heuristic search process may be necessary in order to locate higher-quality and near-optimal solutions. In advancing the science behind the use of metaheuristics for forest planning problems, Pukkala and Heinonen (2006) presented a method for improving the search process of parameters chosen for three metaheuristic techniques, simulated annealing, threshold accepting, and tabu search. Furthermore, Richards and Gunn (2000) described the value of using a strategic oscillation process to diversify the search for near-optimal solutions.
The contribution of this paper is to illustrate the refinement of two standard metaheuristic methods (tabu search and threshold accepting) with the use of alternative reversion rates, to compare outcomes to a metaheuristic that requires reversion (raindrop method), and to describe the effect of reversion on the quality of forest management plans that are subsequently developed.
2 Materials and methods
The methodology associated with this research will be described in this order: a description of the hypothetical forest for which a forest plan is desired, a description of the forest planning problem formulation, a description of the metaheuristic search processes, and a description of the instances for which sets of solutions are generated. Finally, a short description of the statistical tests that are used to determine whether significant differences exist in the sets of solutions that were generated is presented as well as a short description of the computer resources employed.
2.1 Hypothetical forest to which the models are applied
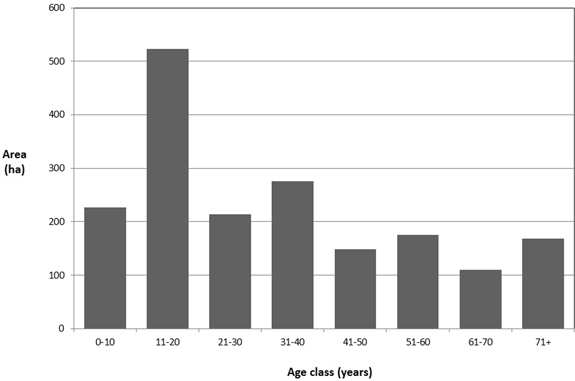
The study area is a 1841 hectare forest that is divided into 87 management units (Fig. 1). It is located in western Oregon (USA), and owned mainly by the State of Oregon. The land area is real, and the stands were delineated by a forester using aerial photography, a topographic map, and a road map. The initial inventory (timber volume) and the age of each stand was however estimated; therefore, the forest is considered hypothetical. Volumes are originally expressed as thousand board feet (MBF) per unit area, yet for this presentation are converted to cubic meters (m3). The age class distribution of the forest is illustrated in Fig. 2, and represents a fairly regulated type of forest with the exception of a large area of 11–20 year-old forests. The target harvest volume for each 5-year time period was assumed to be 32 918.33 m3, which was selected because it was nearly one-half of the volume produced from a relaxed linear programming model (i.e., a model that lacked harvest adjacency constraints and allowed non-integer decisions), and was slightly lower than the sustainable harvest level calculated using the Hanzlik formula (Hanzlik 1922), which assumed a desired 50-year final harvest age. Adjacent stands are defined for the purpose of this research as those that physically share an edge. Thus, there are 210 unique, non-redundant adjacency relationships within this dataset.
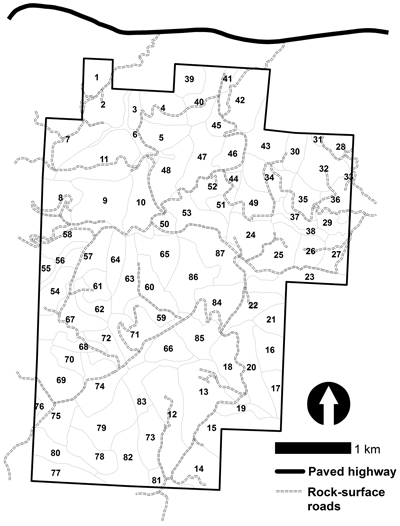
Fig. 1. A map illustrating the layout of stands within the Lincoln Tract in western Oregon (USA).
Fig. 2. The age class distribution of the hypothetical dataset.
2.2 Forest planning problem formulation
In order to demonstrate the effects of using alternative reversion rates on the quality of developed management plans, a single, realistic forest management planning problem for the land was developed. The length of the planning horizon is 30 years. There are six time periods, and each five years in length. The objective function was developed to minimize the squared deviations in the scheduled timber harvest volumes from a target volume:
 where
wheret = a time period
Ht = the total scheduled timber harvest volume during time period t
Tt = the target harvest volume per time period
This is an even-flow (of harvest volume) objective, which seeks to locate the solution that has the closest scheduled harvest volumes in each time period to the target that was selected. A steady flow of harvest volume over time is often recognized as important to forest products industries to ensure full utilization of equipment and labor (Martins et al. 2014). Given the structure of equation 1, the objective function units in this work are therefore (m3)2. To accumulate scheduled harvest volumes, accounting rows were used to acquire the scheduled harvest volume during each time period:
 where
wherei = a management unit (stand)
n = the total number of management units
xit = a binary decision variable representing whether (1) or not (0) management unit i is scheduled for harvest during time period t
vit = the volume available for harvest within management unit i during time period t
Resource constraints were included in the problem formulation to prevent each stand from being harvested more than once during the 30-year time horizon:

j = a management unit (stand)
Ni = the set of all management units (stands) that share an edge with management unit i
There are various ways in which forest harvest adjacency constraints can be formulated. The unit restriction problem is easier to formulate and to generally solve than the area restriction model (Tóth et al. 2012). For this work, we are using pairwise adjacency constraints, which have been shown to perform better in forest planning problems containing overmature and old-growth forests (McDill and Braze 2001). However, Type I non-dominated constraints may be able to shorten solution generation times when solving problems in mixed integer programming format, maximal clique unit restriction adjacency constraints have performed better than pairwise constraints in old-growth forest situations, and new ordinary adjacency matrices may perform better in forest planning problems involving immature forests (McDill and Braze 2000; Manning and McDill 2012). Recently, Manning and McDill (2012) examined two types of adjacency constraints for the unit restriction adjacency problem (pairwise and maximal clique) in an effort to gauge what the optimal parameter settings might be for mixed integer branch and bound solvers. Mean solution times were generally equal to or less when using the pairwise constraints on immature, regulated, and mature forest problems. They also found that an optimal parameter set can generally reduce the time required to solve a problem such as ours, but the time required to determine the optimal parameter set may be extensive (over one day), in general. They further noted that the optimal set of parameters may be specific to each problem being solved, and thus the investment in the parameter tuning process may only be worthwhile if similar problems are to be solved multiple times. Others (e.g., Martins et al. 2005; Goycoolea et al. 2005; Constantino et al. 2008) have applied pairwise, maximal cliques or other types of constraint formulations to the area restriction model of adjacency and clusters or blocked regions of stands. Our example forest problems are composed of a relatively uniform distribution of age classes (neither immature nor over-mature); therefore, they were formulated using a pairwise adjacency constraints. The use of a parameter tuning tool (not employed here) has also been shown to shorten solution generation times (Manning and McDill 2012).
This problem was solved initially using the default parameter settings of the non-linear solver within Lingo 14.0 (Lindo Systems 2013). Since the decision variables were related to the harvest of stands, and since a minimum harvest age was assumed, the problem was reduced to a set of logical variables and irrelevant constraints were removed. The problem thus consisted of 450 variables, 349 of which were integer, and 892 constraints, 12 of which were non-linear. During initial trials using the default parameters within Lingo, it was observed that the global optimum solution could not be located in eight days of processing on a personal computer with a 1.80 GHz Intel® Xeon® E5-2603 processor and 4 Gb of RAM. Therefore, a few parameter settings were adjusted in an effort to decrease the computing time required to solve the problem. The global solver within Lingo was enabled to overcome some of the weaknesses in the default non-linear solver through range bounding and range reduction procedures. With respect to the non-linear solver, the non-linear optimality tolerance was set first to the default (0.0000001), then to 0.02 and 0.05. With respect to the integer solver, the relative optimality tolerance was set first to the default (0.00001), then to 0.02 and 0.05 when the respective non-linear optimality tolerances were changed. The run-time limit for these three attempts at solving the problem was 86 400 seconds (one day).
A very similar problem to this was also solved using mixed integer goal programming, where one adjustment was made to the objective function:
 Through experience we have learned that within a metaheuristic process the squaring of the deviations helps the search process better discern between two solutions that have the same sum of deviations (as in equation 5), yet where one is superior due to its ability to represent a more even distribution of the scheduled harvest volumes over the time periods of the planning horizon. Within mixed integer goal programming, this did not seem to be the case. The planning problem was formulated using integer programming techniques and solved using LINGO 14.0 (Lindo Systems, Inc. 2013). Parameter settings within Lingo were adjusted, as described earlier with the non-linear formulation, and with respect to the integer solver, the relative optimality tolerance was set first to the default (0.00001), and then changed to 0.02 and 0.05. The run-time limit was again 86 400 seconds (one day).
Through experience we have learned that within a metaheuristic process the squaring of the deviations helps the search process better discern between two solutions that have the same sum of deviations (as in equation 5), yet where one is superior due to its ability to represent a more even distribution of the scheduled harvest volumes over the time periods of the planning horizon. Within mixed integer goal programming, this did not seem to be the case. The planning problem was formulated using integer programming techniques and solved using LINGO 14.0 (Lindo Systems, Inc. 2013). Parameter settings within Lingo were adjusted, as described earlier with the non-linear formulation, and with respect to the integer solver, the relative optimality tolerance was set first to the default (0.00001), and then changed to 0.02 and 0.05. The run-time limit was again 86 400 seconds (one day). While our problem seems trivial to solve, a smaller but similar problem, where mixed integer programming was compared against simulated annealing without reversion, was recently reported by Gomide et al. (2013) where they indicated a computing time of about 0.25 to 38 hours might be required for solving the problem formulated with mixed integer programming.
2.3 Metaheuristic search processes
Three different metaheuristic search processes are used to illustrate the effects of reversion on final solution quality. Given that different sets of n-opt decision choices are also employed, the metaheuristic techniques we examined were:
- Tabu search with 1-opt moves
- Tabu search with 1-opt and 2-opt moves
- Tabu search with 1-opt, 2-opt, and 3-opt moves
- Threshold accepting with 1-opt moves
- Threshold accepting with 1-opt, and 2-opt moves
- Threshold accepting with 1-opt, 2-opt and 3-opt moves
- Raindrop method
Each of these techniques uses the following general local search process (for minimization problems):

where
s0 = the initial feasible solution generated
ŝ = the current feasible solution
s' = a proposed new feasible solution
s* = the best feasible solution
Within each iteration of tabu search and the raindrop method, a candidate move (s') is always accepted, and it alters the current solution. In threshold accepting, the proposed candidate may not always be acceptable. Therefore, in the general search process that we provided, the “counter” simply counts acceptable choices made. At some point, depending on the state of the counter, the reversion process occurs. For example, if the reversion interval is 5 acceptable iterations, then after iterations 5, 10, 15, etc. (count mod reversion interval), reversion occurs.
Tabu search is a local search algorithm that was initially developed by Glover (1989, 1990), and has been applied to numerous types of problems, including telecommunications, machine scheduling, and forest management and planning problems not previously mentioned (e.g., Murray and Church 1995). In most cases in forest planning, tabu search has been employed with a 1-opt search process, where a new forest plan is created by changing the status (timing of harvest, choice of management regime, etc.) of one forest management unit. Changes made (moves) are considered off-limit (taboo) for a certain number of iterations of the search, unless aspiration criteria are employed. Aspiration criteria allow the selection of a previously disallowed (taboo) move when the resulting solution is deemed better than any other previously-examined solution. Typically, short-term memory is employed to understand how recent each choice was made and the point at which the tabu status of that choice ends. Longer-term memory can be employed to diversify the search and require the selection of seldom-selected choices. As mentioned, enhancements of tabu search can include the use of a 2-opt search strategy to switch the timing of harvest (or choice of management regime) of two different stands of trees. This process results in a smaller change to the objective function, and can produce plans that might not otherwise be located using similar consecutive 1-opt choices (Bettinger 2008). 3-opt (and greater) moves have been suggested for use in forest planning problems (Bettinger et al. 1999), but due to the amount of time and effort required to build a 3-opt tabu search neighborhood, their use has not been sufficiently explored; as we noted earlier, this really depends on whether the total potential neighborhood is sampled or is partitioned.
Threshold accepting is local search algorithm that was introduced by Dueck and Scheuer (1990). Threshold accepting typically employs 1-opt moves to examine a single randomly-selected change to a current solution, and an acceptance rule that allows inferior solutions to be created as long as the decline in objective function value is within a threshold (using objective function value metrics) of the current or best solution saved in memory. It is similar to simulated annealing, yet with threshold accepting the acceptance rule (and its rate of change) is typically deterministic, rather than stochastic. The behavior of the algorithm can be modeled as a Markov chain, as the sequence of transformations from solution i to solution j has a non-zero probability and only depends on i and j, thus theoretically transition probabilities could be developed for all possible transitions in the search process. Threshold accepting has previously been used in forest management planning (Pukkala and Heinonen 2006; Heinonen et al. 2007; Bettinger and Boston 2008; Zhu and Bettinger 2008a, 2008b) with application to the development of spatially-constrained forest plans.
The raindrop method was initially developed by Bettinger and Zhu (2006) for specific application to forest management and planning problems that have harvest adjacency constraints. Adjacency constraints prevent the harvest of adjacent stands on the landscape for a minimum specified period. Application of the method to other types of problems has provided inferior results (Potter et al. 2009). During the course of a single iteration of the model, a random change is forced into the current solution (a change is made to the status of a forest stand). The infeasibilities are located and the associated forest stands are noted. The stand that is nearest in proximity to the stand associated with this random change is selected (based on the planar, straight-line distance associated with the center of each stand). The infeasibility related to the selected stand is mitigated by deterministically choosing the next best option (e.g., harvest timing) that does not result in an infeasibility with stands located closer to the original randomly-chosen stand nor the original randomly-chosen stand. However, as changes are made, other infeasibilities may arise in association with stands that are located further away from the original stand selected; these changes and their associated infeasibilities are allowed. The process continues by mitigating the infeasibilities associated with the next-closest stand to the original stand, and so on. The process of mitigating infeasibilities radiates outward from the original randomly-chosen stand until there are no more infeasibilities. At that point, one iteration of the model has concluded, and another begins with the random selection of stand and the forceful change of its status. Bettinger and Zhu (2006) concluded that for the type of problem presented here the raindrop method produces superior solutions to other basic s-metaheuristics. However, they also noted that the process of reversion was required every 4 to 5 iterations of the search process. Expansion of this work to a problem that had both wood-flow and area restriction adjacency constraints illustrated a few disadvantages, such as the amount of time required to solve different problems (Zhu et al. 2007).
The sequence of events that are used to transition from one state of the system within the search process to another state does not technically meet the formal definition of a Markov chain process within two of these heuristics. A random process for mapping the transition of states is not used within tabu search, and only a partial random process is used within the raindrop method. Transition probabilities are also not employed in any of the three metaheuristics, therefore no probability distribution is developed to assist in the location of the future state of the system. The future state is determined deterministically or in purely random fashion, depending on the metaheuristic. In this research, we are evaluating the use of a reversion process to interrupt the sequence of events that are used to explore the solution space. Re-initiation of the search process then begins from a high-quality, known starting point.
2.4 Instances for which forest plans are developed
For tabu search and threshold accepting, three different sets of move processes (1-opt; 1-opt and 2-opt; 1-opt, 2-opt and 3-opt) were utilized. Four reversion interval (0, 3, 6 and 9 iterations) were used for each of these methods, based on the conclusions from Bettinger and Zhu (2006) that indicated a reversion rate of 4 or 5 seemed best for the raindrop method. Another way to envision these is that 0 is the lowest rate of reversion (no reversion), and 3 is the highest rate of reversion (every third iteration). While we use the terms (0, 3, 6 and 9 iterations), they could alternatively be viewed as none, 1/3, 1/6, and 1/9. A standard set of 1 million iterations were performed when using the tabu search and raindrop methods. Given the parameters described in Table 1, theoretically 1 million feasible iterations would be performed with threshold accepting as well, although if a sufficient number of unsuccessful (infeasible) moves were attempted, the metaheuristic would terminate prior to the completion of 1 million iterations. Tracking the unsuccessful iterations and forcing the threshold to change allowed the algorithm to complete its work; otherwise, without this, the threshold accepting algorithm would run for a long period of time when the threshold became relatively small. A sufficient number of unsuccessful iterations were allowed, as determined through trial runs of the models, to prevent what seemed to be pre-mature termination of the search process (if too small) and waste (if too large). In Table 2, we describe the parameters that represent the tabu search application. The tabu state was randomly selected between 0 and 200 iterations with each move made during the search process. Through trial runs of the model, we found this to be a better tactic to employ than a simple fixed tabu state. The raindrop method was run for 1 million iterations and 0, 3, 6, and 9 iteration reversion intervals were applied. As we noted earlier, reversion is required with the raindrop method, therefore a reversion interval of 0 (no reversion) was attempted only to illustrate why it is required.
| Table 1. Threshold accepting instances. | |||||||
| Initial threshold | Iterations per threshold | Threshold change | Unsuccessful iterations per threshold | Reversion interval (iterations)a) | 1-opt moves iterationsb) | 2-opt moves iterationsc) | 3-opt moves iterationsd) |
| 10 000 000 | 10 | 100 | 2000 | 0 | ALL | ||
| 10 000 000 | 10 | 100 | 2000 | 3 | ALL | ||
| 10 000 000 | 10 | 100 | 2000 | 6 | ALL | ||
| 10 000 000 | 10 | 100 | 2000 | 9 | ALL | ||
| 10 000 000 | 10 | 100 | 2000 | 0 | 100 | 10 | |
| 10 000 000 | 10 | 100 | 2000 | 3 | 100 | 10 | |
| 10 000 000 | 10 | 100 | 2000 | 6 | 100 | 10 | |
| 10 000 000 | 10 | 100 | 2000 | 9 | 100 | 10 | |
| 10 000 000 | 10 | 100 | 2000 | 0 | 100 | 10 | 3 |
| 10 000 000 | 10 | 100 | 2000 | 3 | 100 | 10 | 3 |
| 10 000 000 | 10 | 100 | 2000 | 6 | 100 | 10 | 3 |
| 10 000 000 | 10 | 100 | 2000 | 9 | 100 | 10 | 3 |
| a) Reversion intervals: 0 = none, 3 = 1/3, 6 = 1/6, and 9 = 1/9 b) If 2-opt or 3-opt iterations are employed, 1-opt iterations are employed at the end of each of these sets c) 2-opt iterations are employed immediately after each set of 100 1-opt iterations d) 3-opt iterations are employed immediately after each set of 10 2-opt iterations | |||||||
| Table 2. Tabu search instances. | ||||
| Number of iterations | Reversion interval (iterations)a) | 1-opt moves iterationsb) | 2-opt moves iterationsc) | 3-opt moves iterationsd) |
| 1 000 000 | 0 | ALL | ||
| 1 000 000 | 3 | ALL | ||
| 1 000 000 | 6 | ALL | ||
| 1 000 000 | 9 | ALL | ||
| 1 000 000 | 0 | 100 | 10 | |
| 1 000 000 | 3 | 100 | 10 | |
| 1 000 000 | 6 | 100 | 10 | |
| 1 000 000 | 9 | 100 | 10 | |
| 1 000 000 | 0 | 100 | 10 | 3 |
| 1 000 000 | 3 | 100 | 10 | 3 |
| 1 000 000 | 6 | 100 | 10 | 3 |
| 1 000 000 | 9 | 100 | 10 | 3 |
| a) Reversion intervals: 0 = none, 3 = 1/3, 6 = 1/6, and 9 = 1/9 b) If 2-opt or 3-opt iterations are employed, 1-opt iterations are employed at the end of each of these sets c) 2-opt iterations are employed immediately after each set of 100 1-opt iterations d) 3-opt iterations are employed immediately after each set of 10 2-opt iterations | ||||
One hundred feasible solutions for each of the 28 metaheuristic processes were generated, each from a random feasible starting solution. Therefore, a total of 2800 solutions (forest plans) were generated in order to examine the effect of the reversion intervals on the results.
2.5 Statistical tests employed
A Mann-Whitney U test and Tamhane’s T2 test were both employed to test the null hypothesis that two different processes produced the same quality samples. Tamhane’s T2 test is the more conservative of the two, yet if the variances of the sets of objective function values are very different, it may allow one to guard against an inflated Type I error. Therefore, it helps us guard against incorrect rejection of the null hypothesis, or in other words the detection of significant effects that really do not exist. In our case, ideally both tests would suggest the same outcome when comparing the means of two different sets of data (objective function values).
Each of the metaheuristics was developed within the HATT environment (Bettinger 2005). HATT 2.0 was developed within Visual Basic 2012, and a personal computer with a 2.50 GHz Intel® Xeon® E5-2609 processor and 8 Gb of RAM was used.
3 Results
The best forest plan that was developed, with respect to the objective noted above, was generated using 1-opt and 2-opt tabu search with a reversion interval of 6 iterations (Table 3). The value of this solution was 0.078, and therefore the scheduled timber harvest volumes for each time period were nearly exactly what were desired. For comparison purposes, the best solution generated using non-linear mixed integer programming methods had a value of 4.80 when the non-linear and integer optimality tolerances were set to 0.05 and the solution generation process was interrupted after one day (84 600 seconds). The solutions values were 9.31 and 15.08 when the optimality tolerances were 0.02 and default levels, respectively. The best mixed integer goal programming solution was 20.71 using the default optimality tolerances. Undaunted by these results, we allowed the Lingo solver (using default parameters) to run for over 2.1 billion iterations using the mixed integer goal programming formulation, and after interrupting the process the best solution generated had a value of 2.31 when the deviations in target volumes (the outcomes) were squared in a post-process manner.
| Table 3. Results of the s-metaheuristic search processes when applied to the forest management problem. | ||||||
| Search process | Reversion interval (iterations) | Minimum (best) solution value (m3)2 | Maximum (worst) solution value (m3)2 | Average solution value (m3)2 | Standard deviation of solution values (m3)2 | Average time required (seconds) |
| RD | 0 | 74 894 | 37 996 939 | 3 620 631 | 6 199 511 | 37.2 |
| RD | 3 | 768 | 47 142 | 10 285 | 8397 | 39.3 |
| RD | 6 | 858 | 34 429 | 7656 | 6704 | 35.7 |
| RD | 9 | 980 | 32 937 | 10 424 | 7690 | 40.7 |
| TA1 | 0 | 7462 | 18 287 902 | 386 149 | 2 072 861 | 15.5 |
| TA1 | 3 | 1119 | 326 233 | 23 120 | 37 113 | 13.2 |
| TA1 | 6 | 1932 | 98 510 | 19 328 | 17 162 | 14.3 |
| TA1 | 9 | 1270 | 360 189 | 22 140 | 37 102 | 17.4 |
| TA12 | 0 | 13 130 | 136 130 | 62 917 | 26 155 | 17.1 |
| TA12 | 3 | 200 | 21 577 | 4026 | 4271 | 14.7 |
| TA12 | 6 | 323 | 29 963 | 6153 | 5457 | 18.5 |
| TA12 | 9 | 991 | 28 465 | 6994 | 5591 | 18.4 |
| TA123 | 0 | 9923 | 330 688 | 68 858 | 39 769 | 29.2 |
| TA123 | 3 | 173 | 34 262 | 5000 | 5463 | 21.1 |
| TA123 | 6 | 329 | 41 796 | 7590 | 6688 | 24.8 |
| TA123 | 9 | 217 | 61 753 | 9032 | 8971 | 25.7 |
| TS1 | 0 | 969 | 517 278 | 20 692 | 63 162 | 98.6 |
| TS1 | 3 | 217 | 1 959 049 | 73 424 | 323 694 | 106.0 |
| TS1 | 6 | 7.406 | 2 205 650 | 33 171 | 238 905 | 102.0 |
| TS1 | 9 | 19.612 | 11 248 | 1158 | 2077 | 112.3 |
| TS12 | 0 | 27.029 | 674 | 329 | 139 | 212.0 |
| TS12 | 3 | 3.625 | 4082 | 206 | 496 | 218.1 |
| TS12 | 6 | 0.078 | 746 | 42 | 111 | 222.3 |
| TS12 | 9 | 0.150 | 440 | 24 | 56 | 225.5 |
| TS123 | 0 | 23.057 | 690 | 323 | 145 | 2219.1 |
| TS123 | 3 | 2.979 | 5273 | 223 | 596 | 2137.1 |
| TS123 | 6 | 0.395 | 462 | 38 | 78 | 2249.5 |
| TS123 | 9 | 0.262 | 251 | 24 | 50 | 2102.4 |
| (m3)2 = Cubic meters of harvest volume squared, the objective function unit value RD = Raindrop method TA1 = Threshold accepting with 1-opt moves only TA12 = Threshold accepting with 1-opt and 2-opt moves TA123 = Threshold accepting with 1-opt, 2-opt and 3-opt moves TS1 = Tabu search with 1-opt moves only TS12 = Tabu search with 1-opt and 2-opt moves TS123 = Tabu search with 1-opt, 2-opt and 3-opt moves Reversion intervals: 0 = none, 3 = 1/3, 6 = 1/6, and 9 = 1/9 | ||||||
The second and third best metaheuristic solutions were generated using 1-opt and 2-opt tabu search with a reversion interval of 9 iterations and 1-opt, 2-opt and 3-opt tabu search with reversion interval of 9 iterations, respectively. The values of second and third best solutions were, respectively 0.150 and 0.262. While these were not quite as good as the best solution generated using 1-opt and 2-opt tabu search with a reversion interval of 6 iterations, the sets of 100 solutions generated were not significantly different when evaluated with the Mann-Whitney U test (p = 0.187 and p = 0.141, respectively) and Tamhane’s T2 test (p = 1.000) from those generated using 1-opt and 2-opt tabu search with a reversion interval of 6 iterations.
The worst forest plan developed was generated using the raindrop method with a reversion interval of 0 iterations; however, we noted earlier that the raindrop method does not work well without a reversion process, which was illustrated in the original raindrop method paper (Bettinger and Zhu 2006). Ignoring this method (raindrop method, reversion interval of 0 iterations), one solution generated by 1-opt threshold accepting with a reversion interval of 0 iterations was clearly very poor, and 3–6% of the solutions generated using 1-opt tabu search (with a reversion interval between 0 and 6 iterations) had objective function values greater than 23 500. The worst result generated by the 1-opt, 2-opt and 3-opt tabu search process with reversion interval of 9 iterations was far better than the best results generated by raindrop method, 1-opt threshold accepting, and other threshold accepting processes with a reversion interval of 0 iterations. In general, regardless of the combination n-opt choices, the worst solutions generated by tabu search improved as the reversion interval increased (reversion rate decreased). This suggests that reversion may be necessary for this metaheuristic, and the search process performed better when it was allowed to explore the solution space longer between reversion points.
There are a number of ways to compare algorithm results, and a statistical analysis of significant differences between mean results is important. We used a random starting point (feasible solution) for each run of each instance of the s-metaheuristics; and thus the assumption was that the best solution from each run could be viewed as a random variable (Golden and Alt 1979; Los and Lardinois 1982). An initial test among the 28 heuristics employed showed that there was a difference among the mean solution values. However, only the raindrop algorithm with no reversion produced a set of solutions that were significantly different (p ≤ 0.05 using both statistical tests) in mean solution values than all other algorithms. All of the tabu search algorithms produced significantly different mean solution values (p ≤ 0.05 using both statistical tests) than the raindrop and threshold accepting algorithms except for 1-opt threshold accepting with no reversion. This was due to the large variance among the 100 samples using 1-opt threshold accepting with no reversion, and thus Tamhane’s T2 test was unable to distinguish a difference among the sets of solution values. Most of the threshold accepting mean solution values were not significantly different (p > 0.05) than the results from the raindrop algorithm, except for the 1-opt and 2-opt threshold accepting with a reversion interval of 9 iterations and 1-opt, 2-opt, and 3-opt threshold accepting with a reversion interval of either 6 or 9 iterations.
The best mean solution was generated by the 1-opt, 2-opt and 3-opt tabu search process that used a reversion interval of 9 iterations, yet the 1-opt and 2-opt tabu search process that used a reversion interval of 9 iterations had nearly an equal mean solution value. These two processes also produced a sets of solution values that had the smallest variation, and the set of solutions generated were not significantly different (p = 0.826 using the Mann-Whitney U test, and p = 1.000 using Tamhane’s T2 test). The standard deviation value of these two processes (50.11 and 55.68 (m3)2), is about half or less of the standard deviation value (111.37 (m3)2) of the 1-opt and 2-opt tabu search process with a reversion interval of 6 iterations (the process that produced the very best solution). When simply examining the tabu search results, regardless of the combination n-opt choices, the variation in solutions generated declined as the reversion interval increased. When examining the 1-opt, 2-opt and 3-opt tabu search results using the Mann-Whitney U test, (a) the solutions generated using a reversion interval of 9 were significantly different (p ≤ 0.05) than those using a reversion interval of 6; (b) the solutions generated using a reversion interval of 6 were significantly different (p ≤ 0.05) than those using a reversion interval of 3; and (c) the solutions generated using a reversion interval of 3 were significantly different (p ≤ 0.05) than those using a reversion interval of 0. However, Tamhane’s T2 test only suggested a significant difference (p ≤ 0.05) in the latter case (c). When examining the 1-opt and 2-opt tabu search results using the Mann-Whitney U test, (a) the solutions generated using a reversion interval of 6 were significantly different (p ≤ 0.05) than those using a reversion interval of 3; and (b) the solutions generated using a reversion interval of 3 were significantly different (p ≤ 0.05) than those using a reversion interval of 0. However, Tamhane’s T2 test suggested no significant differences existed (p > 0.05) for these sets of data. Using both statistical tests, the 1-opt and 2-opt tabu search solutions generated using reversion interval of 6 or 9 were not significantly different (p = 0.187 using the Mann-Whitney U test, p = 0.407 using Tamhane’s T2 test). These results tend to suggest again that reversion was necessary, and the search process performed better when it was allowed to explore the solution space around 6 iterations between reversion points. With threshold accepting and the raindrop method, the variation in solution values was lower with shorter reversion intervals.
When comparing the results regarding average software processing times, threshold accepting produced solutions in 13 to 26 seconds, which was nearly half the time required for a raindrop method solution to be generated, and at least four times as fast as 1-opt tabu search regardless of reversion interval. As expected, 1-opt and 2-opt tabu search was about half as fast as 1-opt tabu search, and 1-opt, 2-opt and 3-opt tabu search was about 20 times slower than 1-opt tabu search regardless of reversion interval. The 1-opt and 2-opt tabu search processes, with reversion intervals of 6 or 9 iterations, generated the better solutions in an average time of about 222 to 225 seconds (about 3.7 minutes). The 1-opt, 2-opt and 3-opt tabu search process with a reversion interval of 9 iterations, which produced the third best solution, required on average about 35 minutes to generate a solution. The reversion intervals seemed to have no impact on the software processing speed. It was apparent that the software processed faster while using the raindrop method and threshold accepting metaheuristics simply due to the characteristics of the search processes (i.e., no neighborhood to assess, as in tabu search). We chose a set of 1-opt, 2-opt and 3-opt choices (Table 2) for tabu search that, if changed, could have a significant effect on software processing speed. For example, increasing the number or frequency (by reducing the number of 1-opt or 2-opt moves) would increase the software processing time due to the need to generate and assess the 3-opt neighborhood more often.
4 Discussion
A reversion process is not a standard aspect of either tabu search nor of threshold accepting processes, although it has been suggested (by Glover and Laguna 1993, 1997) for use in tabu search. The effect of the reversion interval on the results of the tabu search processes is apparent, as is the need to use more than 1-opt moves within both threshold accepting and tabu search. However, with the 1-opt moves alone, the resulting solutions were better and more consistent for tabu search when the reversion interval was 9 iterations. Unfortunately, with 1-opt moves alone and reversion intervals of 3 or 6 iterations, 3–6% of the time the resulting solution was very poor. It seems as if the search could not extract itself from the local optimum, and continuously reverted to that place in the solution space, even though the tabu state was randomly defined between 0 and 200 iterations with each choice made. For threshold accepting, reversion always led to higher quality sets of solutions than when reversion was not employed. For the raindrop method, as we have mentioned, reversion is necessary (Bettinger and Zhu 2006).
The reversion process is, in effect, an intensification of the search through the solution space. The success of the intensified search around high-quality solutions was facilitated by the stochastic nature of move selection within threshold accepting, and the stochastic duration of the tabu state we employed within tabu search. The ability to randomly release from tabu status prevented tabu search from cycling through a small set of common solutions. With standard tabu search, and with the use of a fixed tabu state, this likely would have happened when reversion was applied. Therefore, the stochastic selection of tabu states from values within a pre-defined range facilitated the exploration of different solutions within and around high-quality areas of the solution space when the re-starting point was common and used frequently.
With respect to the amount of effort required to employ a reversion process within a s-metaheuristic, the additional amount of code and logic, at least in this case, amounted to twelve lines of Visual Basic code and two objects on the Visual Basic graphical user interface. One line of code was used to access the reversion interval from the graphical user interface and ten lines of code were developed to determine (a) whether a reversion interval other than 0 was specified, (b) whether it was time to revert, based on the number of search process iterations, (c) to change the current harvest schedule to the best schedule saved in memory, and (d) to change the total current scheduled volumes to the best scheduled volumes saved in memory. An additional five lines of Visual Basic code were necessary to instruct the program to change the value of the reversion interval when a user changed the value on the graphical user interface.
While our analysis of the effects of reversion on s-metaheuristics was limited to one case study and a small set of search parameters, the results are compelling enough to suggest that this process would be a valuable addition for s-metaheuristics where it is normally or typically not employed. Certainly, we could have examined the effects of reversion on other metaheuristic processes, on other forestry problems (or problems of other fields), or in conjunction with other sets of search parameters. Each metaheuristic has a general behavior (stochastic, deterministic, or both in the case of the raindrop method) with regard to how it explores the solution space in search of the optimal solution to a problem. Li et al. (2009), without investigating reversion, illustrated the promise of combining the search behavior of the metaheuristic processes used here (tabu search, threshold accepting, raindrop method). From this previous work it was suggested that a relatively fast heuristic (e.g., threshold accepting) might be used to transition from a random starting point to a very good solution, before another process (tabu search, raindrop method) is used to refine the solution. Further work might thus explore the use of n-opt moves, reversion, and the combined behavior of the s-metaheuristics.
5 Conclusions
A reversion process was incorporated into two s-metaheuristics (tabu search and threshold accepting). The process was based simply on the amount of time (as represented by search process iterations) that had passed during the search for the optimal solution to a forest planning problem. The reversion process involved re-starting a metaheuristic from a known, high-valued local optima, the best solution (s*) stored in memory at the time the reversion was employed. This intensification of the search process was facilitated by the stochastic nature of move selection within threshold accepting and the stochastic selection of tabu states within tabu search. In addition, n-opt move combinations were incorporated within tabu search and threshold accepting. As others have found, the use of 2-opt and 3-opt moves can improve the solutions generated with s-metaheuristics. We have also demonstrated the value of periodically reverting to the best solution stored in memory. The results suggested that reversion may be a necessary aspect within tabu search and threshold accepting, and that the search processes performed better when they were allowed to explore the solution space for around 6 iterations between reversion points.
Acknowledgements
This work was supported by McIntire-Stennis project number GEOZ-0168-MS through the Warnell School of Forestry and Natural Resources at the University of Georgia. This work was also supported by the Government of Turkey in accordance with the “Regulation on Civil Servants to be Sent Abroad for Training” published in the Official Gazette dated 01/02/1974 No. 14786.
References
Bettinger P. (2005). HATT: the heuristic algorithm teaching tool for advanced forest planning courses. In: Bevers M., Barrett T.M. (comps.). Systems analysis in forest resources: proceedings of the 2003 symposium. U.S. Department of Agriculture, Forest Service, Pacific Northwest Research Station, General Technical Report PNW-GTR-656. p. 61–70.
Bettinger P. (2008). Tabu search experience in forest management and planning. In: Jaziri W. (ed.). Local search techniques: focus on tabu search. IN-TECH Education and Publishing KG, Vienna. p. 199–208.
Bettinger P., Boston K. (2008). Habitat and commodity production trade-offs in Coastal Oregon. Socio-Economic Planning Sciences 42: 112–128. http://dx.doi.org/10.1016/j.seps.2006.11.001.
Bettinger P., Chung W. (2004). The key literature of, and trends in, forest-level management planning in North America, 1950–2001. The International Forestry Review 6: 40–50. http://dx.doi.org/10.1505/ifor.6.1.40.32061.
Bettinger P., Zhu J. (2006). A new heuristic for solving spatially constrained forest planning problems based on mitigation of infeasibilities radiating outward from a forced choice. Silva Fennica 40: 315–333. http://dx.doi.org/10.14214/sf.477.
Bettinger P., Sessions J., Boston K. (1997). Using Tabu search to schedule timber harvests subject to spatial wildlife goals for big game. Ecological Modelling 94: 111–123. http://dx.doi.org/10.1016/S0304-3800(96)00007-5.
Bettinger P., Sessions J., Johnson K.N. (1998). Ensuring the compatibility of aquatic habitat and commodity production goals in eastern Oregon with a Tabu search procedure. Forest Science 44: 96–112.
Bettinger P., Boston K., Sessions J. (1999). Intensifying a heuristic forest harvest scheduling search procedure with 2-opt decision choices. Canadian Journal of Forest Research 29: 1784–1792. http://dx.doi.org/10.1139/x99-160.
Bettinger P., Graetz D., Boston K., Sessions J., Chung W. (2002). Eight heuristic planning techniques applied to three increasingly difficult wildlife planning problems. Silva Fennica 36: 561–584. http://dx.doi.org/10.14214/sf.545.
Bettinger P., Boston K., Kim Y.-H., Zhu J. (2007). Landscape-level optimization using tabu search and stand density-related forest management prescriptions. European Journal of Operational Research 176: 1265–1282. http://dx.doi.org/10.1016/j.ejor.2005.09.025.
Borges J.G., Hoganson H.M., Rose D.W. (1999). Combining a decomposition strategy with dynamic programming to solve spatially constrained forest management scheduling problems. Forest Science 45: 201–212.
Borges J.G., Garcia-Gonzalo J., Bushenkov V., McDill M.E., Marques S., Oliveria M.M. (2014a). Addressing multicriteria forest management with Pareto frontier methods: an application in Portugal. Forest Science 60: 63–72. http://dx.doi.org/10.5849/forsci.12-100.
Borges P., Bergseng E., Eid T. (2014b). Adjacency constraints in forestry – a simulated annealing approach comparing different candidate solution generators. Mathematical and Computational Forestry & Natural-Resource Sciences 6: 11–25.
Boston K., Bettinger P. (1999). An analysis of Monte Carlo integer programming, simulated annealing, and tabu search heuristics for solving spatial harvest scheduling problems. Forest Science 45: 292–301.
Boston K., Bettinger P. (2006). An economic and landscape evaluation of the green-up rules for California, Oregon, and Washington (USA). Forest Policy and Economics 8: 251–266. http://dx.doi.org/10.1016/j.forpol.2004.06.006.
Brumelle S., Granot D., Halme M., Vertinsky I. (1998). A tabu search algorithm for finding good forest harvest schedules satisfying green-up constraints. European Journal of Operational Research 106: 408–424. http://dx.doi.org/10.1016/S0377-2217(97)00282-8.
Caro F., Constantino M., Martins I., Weintraub A. (2003). A 2-opt tabu search procedure for the multi-period forest harvesting problem with adjacency, greenup, old growth, and even flow constraints. Forest Science 49: 738–751.
Constantino M., Martins I., Borges J.G. (2008). A new mixed integer programming model for harvest scheduling subject to maximum area restrictions. Operations Research 56: 542–551. http://dx.doi.org/10.1287/opre.1070.0472.
Cordeau J.-F., Maischberger M. (2012). A parallel iterated tabu search heuristic for vehicle routing problems. Computers & Operations Research 39: 2033–2050. http://dx.doi.org/10.1016/j.cor.2011.09.021.
Crowe K., Nelson J. (2003). An indirect search algorithm for harvest scheduling under adjacency constraints. Forest Science 49: 1–11.
Dueck G., Scheuer T. (1990). Threshold accepting: a general purpose optimization algorithm appearing superior to simulated annealing. Journal of Computational Physics 90: 161–175. http://dx.doi.org/10.1016/0021-9991(90)90201-B.
Falcão A.O., Borges J.G. (2001). Designing an evolution program for solving integer forest management scheduling models: an application in Portugal. Forest Science 47: 158–168.
Falcão A.O., Borges J.G. (2002). Combining random and systematic search heuristic procedures for solving spatially constrained forest management scheduling problems. Forest Science 48: 608–621.
Fischer A., Fischer F., Jäger G., Keilwagen J., Molitor P., Grosse I. (2014). Exact algorithms and heuristics for the Quadratic Traveling Salesman Problem with an application in bioinformatics. Discrete Applied Mathematics 166: 97–114. http://dx.doi.org/10.1016/j.dam.2013.09.011.
Galperin E.A. (2006). Reflections on optimality and dynamic programming. Computers and Mathematics with Applications 52: 235–257. http://dx.doi.org/10.1016/j.camwa.2006.08.015.
Glover F. (1989). Tabu search – Part I. ORSA Journal on Computing 1: 190–206.
Glover F. (1990). Tabu search – Part II. ORSA Journal on Computing 2: 4–32.
Glover F., Laguna M. (1993). Tabu search. In: Reeves C.R. (ed.). Modern heuristic techniques for combinatorial problems. John Wiley & Sons, Inc., New York. p. 70–150.
Glover F., Laguna M. (1997). Tabu search. Kluwer Academic Publishers, Boston. 382 p.
Golden B.L., Alt F.B. (1979). Interval estimation of a global optimum for large combinatorial problems. Naval Research Logistics Quarterly 26: 69–77.
Gomide L.R., Arce J.E., da Silva A.C.L. (2013). Comparação entre a meta-heurística simulated annealing e a programação linear inteira no agendamento da colheita florestal com restrições de adjacência. Ciência Florestal 23: 451–462.
Goycoolea M., Murray A.T., Barahona F., Epstein R., Weintraub A. (2005). Harvest scheduling subject to maximum area restrictions: exploring exact approaches. Operations Research 53: 490–500. http://dx.doi.org/10.1287/opre.1040.0169.
Hanzlik E.J. (1922). Determination of the annual cut on a sustained basis for virgin American forests. Journal of Forestry 20: 611–625.
Härtl F., Hahn A., Knoke T. (2013). Risk-sensitive planning support for forest enterprises: the YAFO model. Computers and Electronics in Agriculture 94: 58–70. http://dx.doi.org/10.1016/j.compag.2013.03.004.
Heinonen T., Pukkala T. (2004). A comparison of one- and two-compartment neighbourhoods in heuristic search with spatial forest management goals. Silva Fennica 38: 319–332. http://dx.doi.org/10.14214/sf.419.
Heinonen T., Kurttila M., Pukkala T. (2007). Possibilities to aggregate raster cells through spatial optimization in forest planning. Silva Fennica 41: 89–103. http://dx.doi.org/10.14214/sf.474.
Heinonen T., Pukkala T., Ikonen V.-P., Peltola H., Gregow H., Venäläinen A. (2011). Consideration of strong winds, their directional distribution and snow loading in wind risk assessment related to landscape level forest planning. Forest Ecology and Management 261: 710–719. http://dx.doi.org/10.1016/j.foreco.2010.11.030.
Hillier F.S., Lieberman G.J. (1980). Introduction to operations research. Holden-Day, Inc., San Francisco, CA. 829 p.
Li G., Wang Y. (2014). Global optimality conditions for nonlinear programming problems with linear equality constraints. Journal of Applied Mathematics Article ID 213178. 5 p. http://dx.doi.org/10.1155/2014/213178.
Li R., Bettinger P., Boston K. (2010). Informed development of meta heuristics for spatial forest planning problems. The Open Operational Research Journal 4: 1–11. http://benthamopen.com/ABSTRACT/TOORJ-4-1.
Liittschwager J.M., Tcheng T.H. (1967). Solution of a large-scale forest scheduling problem by linear programming decomposition. Journal of Forestry 65: 644–646.
Limaei S.M., Kouhi M.S., Sharaji T.R. (2014). Goal programming approach for sustainable forest management (case study in Iranian Caspian forests). Journal of Forestry Research 25: 429–435. http://dx.doi.org/10.1007/s11676-014-0472-z.
Lindo Systems, Inc. (2013). Extended LINGO / Win32, Release 14.0.1.58. Lindo Systems, Inc., Chicago, IL.
Los M., Lardinois C. (1982). Combinatorial programming, statistical optimization and the optimal transportation network problem. Transportation Research Part B: Methodological 16: 89–124. http://dx.doi.org/10.1016/0191-2615(82)90030-3.
Manning P.J., McDill M.E. (2012). Optimal parameter settings for solving harvest scheduling models with adjacency constraints. Mathematical and Computational Forestry & Natural-Resource Sciences 4: 16–26.
Martins I., Constantino M., Borges J.G. (2005). A column generation approach for solving a non-temporal forest harvest model with spatial structure constraints. European Journal of Operational Research 161: 478–498. http://dx.doi.org/10.1016/j.ejor.2003.07.021.
Martins I., Ye M., Constantino M., da Conceição Fonesca M., Cadima J. (2014). Modeling target volume flows in forest harvest scheduling subject to maximum area restrictions. TOP 22: 343–3625. http://dx.doi.org/10.1007/s11750-012-0260-x.
Matusiak M., de Koster R., Kroon L., Saarinen J. (2014). A fast simulated annealing method for batching precedence-constrained customer orders in a warehouse. European Journal of Operational Research 236: 968–977. http://dx.doi.org/10.1016/j.ejor.2013.06.001.
McDill M.E., Braze J. (2000). Comparing adjacency constraint formulations for randomly generated forest planning problems with four age-class distributions. Forest Science 46: 423–436.
McDill M.E., Braze J. (2001). Using the branch and bound algorithm to solve forest planning problems with adjacency constraints. Forest Science 47: 403–418.
Murray A.T. (1999). Spatial restrictions in forest planning. Forest Science 45: 45–52.
Murray A.T., Church R.L. (1995). Measuring the efficacy of adjacency constraint structure in forest planning models. Canadian Journal of Forest Research 25: 1416–1424. http://dx.doi.org/10.1139/x95-154.
Nelson J. (2003). Forest-level models and challenges for their successful application. Canadian Journal of Forest Research 33: 422–429. http://dx.doi.org/10.1139/X02-212.
Potter W.D., Drucker E., Bettinger P., Maier F., Martin M., Luper D., Watkinson M., Handy G., Hayes C. (2009). Diagnosis, configuration, planning, and pathfinding: experiments in nature-inspired optimization. In: Chiong R., Dhakal S. (eds.). Natural intelligence for scheduling, planning and packing problems. Springer, Berlin. p. 267–294.
Pukkala T., Heinonen T. (2006). Optimizing heuristic search in forest planning. Nonlinear Analysis: Real World Applications 7: 1284–1297. http://dx.doi.org/10.1016/j.nonrwa.2005.11.011.
Richards E.W., Gunn E.A. (2000). A model and tabu search method to optimize stand harvest and road construction schedules. Forest Science 46: 188–203.
Sağlam B., Salman F.S., Sayın S., Türkay M. (2006). A mixed-integer programming approach to the clustering problem with an application in customer segmentation. European Journal of Operational Research 173: 866–879. http://dx.doi.org/10.1016/j.ejor.2005.04.048.
Seo J-H., Vilcko F., Sanchez Orois S., Kunrh S., Son Y.-M., Gadow K.v. (2005). A case study of forest management planning using a new heuristic algorithm. Tree Physiology 25: 929–938. http://dx.doi.org/10.1093/treephys/25.7.929.
Sinclair K., Cordeau J.-F., Laporte G. (2014). Improvements to a large neighborhood search heuristic for an integrated aircraft and passenger recovery problem. European Journal of Operational Research 233: 234–245. http://dx.doi.org/10.1016/j.ejor.2013.08.034.
Talbi E.-G. (2009). Metaheuristics. From design to implementation. John Wiley & Sons, Hoboken, NJ. 593 p.
Tóth S., McDill M.E., Könnyű N., George S. (2012). A strengthening procedure for the path formulation of the area-based adjacency problem in harvest scheduling models. Mathematical and Computational Forestry & Natural-Resources Sciences 4: 27–49.
Wei Y., Hoganson H.M. (2008). Tests of a dynamic programming-based heuristic for scheduling forest core area production over large landscapes. Forest Science 54: 367–380.
Zhu J., Bettinger P. (2008a). Assessment of three heuristics for developing large-scale spatial forest harvest scheduling plans. Journal of Applied Sciences 8: 4113–4120. http://dx.doi.org/10.3923/jas.2008.4113.4120.
Zhu J., Bettinger P. (2008b). Estimating the effects of adjacency and green-up constraints on landowners of different sizes and spatial arrangements located in the southeastern U.S. Forest Policy and Economics 10: 295–302. http://dx.doi.org/10.1016/j.forpol.2007.11.006.
Zhu J., Bettinger P., Li R. (2007). Additional insight into the performance of a new heuristic for solving spatially constrained forest planning problems. Silva Fennica 41: 687–698. http://dx.doi.org/10.14214/sf.276.
Total of 65 references