Modelling the effect of habitat composition and roads on the occurrence and number of moose damage at multiple scales
Nikula A., Nivala V., Matala J., Heliövaara K. (2019). Modelling the effect of habitat composition and roads on the occurrence and number of moose damage at multiple scales. Silva Fennica vol. 53 no. 1 article id 9918. https://doi.org/10.14214/sf.9918
Highlights
- The occurrence and number of moose damage were modelled with a zero-inflated count model
- An admixture of mature forests within plantations increased the number of damage
- Vicinity of inhabited areas and roads reduced damage
- Plantations in landscapes with a large amount of pine-dominated thinning forests had less damage in Lapland
- Damage risk assessment should include characteristics specific to each region.
Abstract
We modelled the effect of habitat composition and roads on the number and occurrence of moose (Alces alces L.) damage in Ostrobothnia and Lapland using a zero-inflated count model. Models were developed for 1 km2, 25 km2 and 100 km2 landscapes consisting of equilateral rectangular grid cells. Count models predict the number of damage, i.e. the number of plantations and zero models the probability of a landscape being without damage for a given habitat composition. The number of moose damage in neighboring grid cells was a significant predictor in all models. The proportion of mature forest was the most frequent significant variable, and an increasing admixture of mature forests among plantations increased the number and occurrence of damage. The amount of all types of plantations was the second most common significant variable predicting increasing damage along with increasing amount of plantations. An increase in thinning forests as an admixture also increased damage in 1 km2 landscapes in both areas, whereas an increase in pine-dominated thinning forests in Lapland reduced the number of damage in 25 km2 landscapes. An increasing amount of inhabited areas in Ostrobothnia and the length of connecting roads in Lapland reduced the number of damage in 1 and 25 km2 landscapes. Differences in model variables between areas suggest that models of moose damage risk should be adjusted according to characteristics that are specific to the study area.
Keywords
forestry;
Alces alces;
damage probability;
forest damage;
forest plantation;
habitat selection;
habitat modelling;
zero-inflated negative binomial distribution
-
Nikula,
Natural Resources Institute Finland (Luke), Bioeconomy and Environment, Ounasjoentie 6, FI-96200 Rovaniemi, Finland
E-mail
ari.nikula@luke.fi

- Nivala, Natural Resources Institute Finland (Luke), Bioeconomy and Environment, Ounasjoentie 6, FI-96200 Rovaniemi, Finland E-mail vesa.nivala@luke.fi
- Matala, Natural Resources Institute Finland (Luke), Natural resources, Yliopistokatu 6, FI-80100 Joensuu, Finland E-mail juho.matala@luke.fi
- Heliövaara, University of Helsinki, Department of Forest Sciences, P.O. Box 27, FI-00014 University of Helsinki, Finland E-mail kari.heliovaara@helsinki.fi
Received 27 November 2017 Accepted 7 January 2019 Published 10 January 2019
Views 184015
Available at https://doi.org/10.14214/sf.9918 | Download PDF

Supplementary Files
1 Introduction
Moose (Alces alces L.) population densities in Fennoscandian countries have been probably the highest in the world since 1970s (Lavsund et al. 2003). High moose population has led to substantial moose damage in forests and the amount of damage has remained high until the 2000s (Lavsund et al. 2003). In Finland in 2004–2008, moose damage was recorded in a total of 741 000 ha corresponding to 19% of all plantations and 24% of pine-dominated plantations (Korhonen et al. 2010). Severe damage was recorded in 3% of pine-dominated plantations. In Sweden, the amount of fresh (1–3 yrs old) moose damage varied between 12–15% of Scots pine and 9–44% of birch plantations during the years 2004–2013 (Swedish Statistical Yearbook… 2013).
Moose cause damage to trees by browsing leader and lateral shoots which leads to growth losses and impaired timber quality (Lavsund 1987; Bergqvist et al. 2001; Wallgren et al. 2014). The majority of damage occurs in winter when food sources other than trees are under snow cover. Moose browse on several tree species, such as birch (Betula pendula Roth and B. pubescens Ehrh.), aspen (Populus tremula L.), willows (Salix spp.) and juniper (Juniperus communis L.) (Bergström and Hjeljord 1987; Månsson et al. 2007), but in economic terms, Scots pine (Pinus sylvestris L.) is the most important tree species affected by moose (Lavsund 1987).
Moose have annual home ranges varying from some hundreds of hectares to some thousands of hectares (Sweanor and Sandegren 1989; Cederlund and Sand 1994). At least the northern part of the moose population in Fennoscandia is migratory (Ball et al. 2001), and average distances between summer and winter home ranges have been measured to range from a few kilometres to some tens of kilometres (Sweanor and Sandegren 1988; Ball et al. 2001). Moose have been shown to be selective in their home range selection (Nikula et al. 2004; Cassing et al. 2006), and there is evidence that moose are selective also within their home ranges (Cederlund and Okarma 1988; Ball et al. 2001; Nikula et al. 2004). As a consequence, when assessing factors influencing moose damage risk landscape sizes corresponding to the home range size of moose should be addressed.
In summer moose are capable of using a large variety of habitats due to their ability to browse on numerous plant species (Cederlund et al. 1980). In winter, when fewer plants are available due to snow cover and when deciduous trees are bare, moose are more selective than in summer and use areas characterised by a mosaic of young and older forests (Bjørneraas et al. 2012). Stands with an age class of less than 30 years are usually preferred by moose (Månsson et al. 2011) and especially pine-dominated young stands seem to characterise moose winter pastures (Nikula et al. 2004). From the point of view of moose damage risk, it can thus be hypothesized that if preferred habitats are not evenly distributed at the landscape or regional level, it leads to uneven use of habitats and, consequently, uneven distribution of damage.
Studies of moose damage at national and regional levels have shown that changes in moose populations are also reflected in changes in browsing of preferred tree species and damage to pine stands (Hörnberg 2001a). Moose density index has been found to be positively correlated with browsing pressure on Scots pine also at the local scale but no evidence of density dependent habitat selection (Månsson 2009) nor correlation between population level and damage level at regional scale (Hörnberg 2001b) have been found. Instead, significant correlation between the availability of browse species and browsing intensity of the most preferred food sources have been found at regional (Hörnberg 2001a) and at landscape levels similar to or larger than the home range size of moose (Cassing et al. 2006). In addition, moose habitat selection often includes trade-off situations where moose behaviour is constrained by e.g. human activity (Bjørneraas et al. 2011). Therefore, in addition to the availability of preferred habitats also disturbance factors potentially affect moose damage risk.
Qualitative factors affecting moose resource selection and damage at the local, home range and landscape levels are fairly well known, but only a few studies have assessed damage risk quantitatively. The aim of this study was to develop models for the occurrence and number of moose damage by using located moose damage data as a response variable and habitat composition as well as other landscape features as explanatory variables. In this study, we concentrate on factors ranging from the local to landscape and regional levels influencing the occurrence and number of damage.
2 Material and methods
2.1 Study areas
The study was conducted in Finland in southern Lapland and western Northern Ostrobothnia (later referred to as Ostrobothnia, Fig. 1). The northernmost border of the study area in Lapland approximately follows the line where mountainous areas and non-private land start to prevail. To the east and west, the Lapland study area is delimited by the Finnish-Russian and Finnish-Swedish borders, respectively. In Ostrobothnia, the easternmost border of the study area is approximately delineated by a topographic border formed by the highest shoreline after the last glacial period (200–220 m a.s.l., Ojala et al. 2013), and the Gulf of Bothnia in the west. The area is restricted by the provincial southern border of Ostrobothnia and the Lapland border in the north. The main tree species in both study areas are Scots pine, Norway spruce (Picea abies (L.) Karst.) and birches. The shrub layer consists of different willow species and juniper.
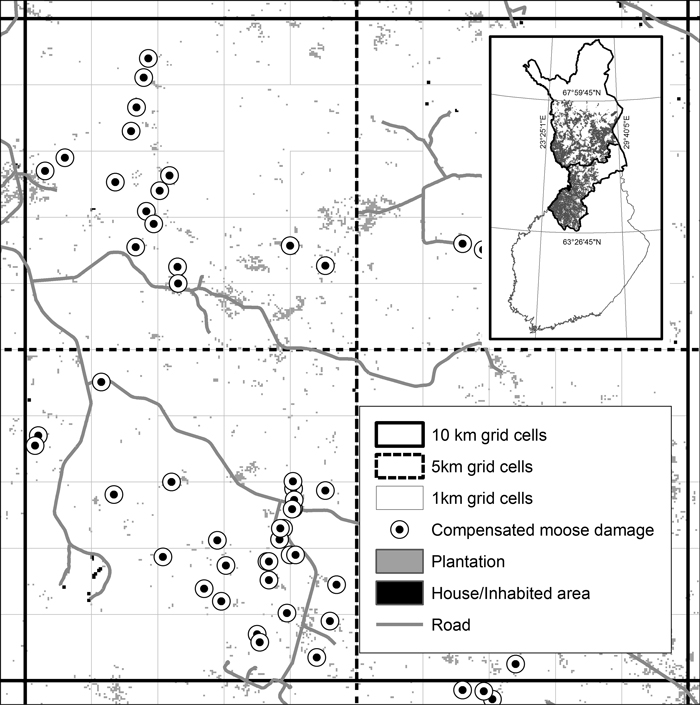
Fig. 1. An illustration of the study setup. Grid cells of 1 km, 5 km and 10 km were overlaid on located moose damage and land use and forest classification (for a complete list of variables see Tables 1a,b). Grey areas on the index map show the location of privately owned land in the study area and bolded lines delineate the provinces of Ostrobothnia and Lapland.
The Ostrobothnia study area lies in the middle boreal region (Ahti et al. 1968). The terrain is rather flat, consisting of the mosaic of mineral soils and peatlands, as well as anthropogenically fragmented areas, mostly agricultural land. About 50% of forestry land comprises peatland, of which about 60% have been drained (Finnish Statistical Yearbook… 2011). About 60% of the forest land is owned by private forest owners and most of the forests are commercially managed. The period of permanent snow cover lasts from mid-November to the end of April, and the maximum depth of snow cover is 40–60 cm (Pirinen et al. 2012).
The southern and south-western parts of the Lapland study area belong to mid-boreal region, whereas the eastern and northern parts belong to the northern boreal region (Ahti et al. 1968). About one third of the forestry land is privately owned, and most of the forests are commercially managed. The majority of privately owned land is located along the Kemi and Tornio rivers and their arteries. The period of permanent snow cover lasts from the beginning of October to mid-May, and the maximum depth of snow cover is 60–90 cm (Pirinen et al. 2012).
2.2 Moose damage data
Moose damage data consisted of located data on damaged plantations for which forest owners were compensated during the years 2002–2008. In Finland, the state pays compensation for moose damage to private forest owners for growth and quality losses and for possible regeneration costs (Finlex 2014). The area of damage must be ≥0.1 ha and the calculated damage has to exceed 170 euros. Compensation is paid only if the damage is less than three years old and it cannot be paid for the same plantation until three years has passed since earlier compensation. There were total of 2663 plantations in Ostrobothnia and 1287 plantations in Lapland that had been compensated for in 2002–2008 in our data. The total area of compensated plantations varied annually from 377 ha to 1831 ha in Ostrobothnia and from 367 ha to 1237 ha in Lapland during the study period. The average damage area per compensated plantation varied annually between 1.6–7.9 ha in Ostrobothnia and 1.1–5 ha in Lapland.
2.3 Landscape data
Land use and forest data for the analysis were provided by the Finnish National Forest Inventory (NFI). In Finland, the NFI utilizes Landsat and Spot satellite images concurrently with field plots, as well as digital maps of roads, agricultural land and other non-forest land, to separate non-forest land from forest land. The Multi-Source National Forest Inventory method (MS-NFI) (Tomppo et al. 2008) uses the k-nn method for producing estimates of e.g. timber volume for each tree species and for each pixel corresponding to a 25 × 25 m land area. The MS-NFI data used in the analyses correspond to the year 2005.
Digital maps of timber volume estimates for pine, spruce and deciduous trees, as well as digital maps of fields, settlements, roads, waters and peatlands, were imported to a geographic information system (GIS) as separate layers. For the analysis, we combined timber volume layers and other land use layers to a single land use and cover layer using total timber volume as a proxy of forest development stage (Tomppo et al. 1998). Drained peatlands were separated from non-drained peatlands with the aid of digital maps of peatlands and digitized ditches (source National Survey of Land). In the resulting data each pixel can belong to one of 15 classes (Table 1a). Digital maps of roads (source Finnish Transport Agency, FTA) were classified in four road classes according to the road class definitions of the FTA (Table 1a).
| Table 1a. Original land use and road classification was formed of 19 classes whose criteria are shown in right column (Variabes #1–19). Middle column gives a description of habitat type, land use and cover type and road class. | |||
| Var# | Acronym | Habitat-, land use- or road class | Criteria |
| 1 | OPENMIN | Treeless areas on mineral soil | Mineral soil, total tree volume ≤4 m3 ha–1 |
| 2 | OPENPEAT | Treeless areas on peatland | Peatland, total tree volume ≤4 m3 ha–1 |
| 3 | PINEPLAMIN | Pine-dominated plantations on mineral soil | Mineral soil, total tree volume 5–42 m3 ha–1 |
| 4 | PINEPLAPEATND | Pine-dominated plantations on non-drained peatland | Peatland, non-drained, total tree volume 5–42 m3 ha–1 |
| 5 | PINEPLAPEATDR | Pine-dominated plantations on drained peatland | Peatland, drained, total tree volume 5–42 m3 ha–1 |
| 6 | OTHERPLANT | Non-pine-dominated plantations on mineral soil or on either drained or non-drained peatland | Mineral soil and peatland, non-drained and drained, total tree volume 5–42 m3 ha–1 |
| 7 | PINETHIMIN | Young pine-dominated thinning forests on mineral soil | Mineral soil, total tree volume 43–81 m3 ha–1 |
| 8 | PINETHIPEATND | Young pine-dominated thinning forests on non-drained peatland | Peatland, non-drained, total tree volume 43–81 m3 ha–1 |
| 9 | PINETHIPEATDR | Young pine-dominated thinning forests on drained peatland | Peatland, drained, total tree volume 43–81 m3 ha–1 |
| 10 | OTHERTHI | Non-pine-dominated thinning forests on mineral soil or on either drained or on non-drained peatland | Mineral and peatland, non-drained and drained, total tree volume 43–81 m3 ha–1 |
| 11 | MATURE | Advanced thinning forests and mature forests on mineral soil or on either drained or non-drained peatland | Mineral and peatland, non-drained and drained, total tree volume >81 m3 ha–1 |
| 12 | WATER | Water | Classified as water in MS-NFI data |
| 13 | INHABITED | Inhabited area | Classified as inhabited area in MS-NFI data |
| 14 | AGRI | Agricultural field | Classified as agricultural in MS-NFI data |
| 15 | MANMADE | Other man-made | Classified as other man-made in MS-NFI data |
| 16 | MAINROAD | Motorways and main roads | Finnish Transport Agency (FTA) class I and class II main roads in national road classification, >8 m wide, asphalt pavement |
| 17 | REGROAD | Regional roads | FTA regional roads, 5–6.5 m wide, asphalt and oil gravel pavement |
| 18 | CONNROAD | Connecting roads | FTA connecting roads, 4–5 m wide, mainly asphalt and oil gravel pavement |
| 19 | FORROAD | Forestry road | FTA functional classes 5 and 6, gravel |
2.4 Grid based modelling
We superimposed three grids sized 1 × 1 km, 5 × 5 km and 10 × 10 km on the study area and then calculated the number of compensated moose damage plantations in each grid cell and used this as the response variable. Hereafter, the cell sizes are referred to as 1 km2, 25 km2 and 100 km2 cells and landscapes, respectively. Due to there being several owner groups other than private land owners, we used the following criteria for selecting grid cells for inclusion in modelling: 1) privately owned forest land had to be >50% of the area, 2) there had to be >0.5 ha of privately owned plantations per cell, and 3) after removing grid cells not fulfilling the previous criteria, the remaining cells had additionally to have a minimum of two adjacent grid cells. The number of grid cells per cell size and study area used in modelling together with the means, S.D. and medians of independent variables are presented in Supplementary files S1a,b and S2a,b. The total number of damaged plantations used in modelling varies among cell sizes due to the criteria used in selecting cells for modelling. For each grid cell we calculated the proportion of each land use and forest class (Table 1a) using Fragstats (McGarigal and Marks 1995) and the length of each road class with ArcMap 10.1 (Environmental Systems Research… 2012). For modelling we also calculated the sum of different combinations of original variables (later referred to as sum variables) in each grid cell (Table1b). Both the original as well as the sum variables were used as explanatory variables in modelling.
| Table 1b. In the different steps of modelling further variables #20–32 were formed by summing the original classes (right column). Middle column gives a description of habitat type, land use and cover type and road class. The average number of damage per year in neighboring cells (NNDAMAGE) was forced to both the count and zero models at each step and to the final models. | |||
| Var# | Acronym | Habitat-, land use- or road class | Criteria |
| 20 | FORESTSUM | Sum of all types of forests | Sum of variables #3–11 |
| 21 | MANMADESUM | Sum of man-made areas on non-forestry land | INHABITED + AGRI + MANMADE |
| 22 | PLANTSUM | Sum of all plantations | PINEPLAMIN + PINEPLAPEATND + PINEPLAPEATDR + OTHERPLANT |
| 23 | PINEPLANTSUM | Sum of pine-dominated plantations on mineral soil and peatlands | PINEPLAMIN + PINEPLAPEATND + PINEPLAPEATDR |
| 24 | PINEPLANTPEAT-SUM | Sum of pine-dominated plantations on peatlands | PINEPLAPEATND + PINEPLAPEATDR |
| 25 | THINNSUM | Sum of all thinning forests | PINETHIMIN + PINETHIPEATND + PINETHIPEATDR + OTHERTHI |
| 26 | PINETHINNSUM | Sum of pine dominated thinning forests | PINETHIMIN + PINETHIPEATND + PINETHIPEATDR |
| 27 | PINETHINNPEAT-SUM | Sum of pine-dominated thinning forests on peatlands | PINETHIPEATND + PINETHIPEATDR |
| 28 | PINEPEATSUM | Sum of pine-dominated plantations and thinning forests on peatlands | PINEPLAPEATND + PINEPLAPEATDR + PINETHIPEATND + PINETHIPEATDR |
| 29 | PINEDRSUM | Sum of pine-dominated plantations and thinning forests on drained peatlands | PINEPLAPEATDR + PINETHIPEATDR |
| 30 | PINENDSUM | Sum of pine-dominated younger forests on non-drained peatlands | PIENPLAPEATND + PINETHIPEATND |
| 31 | PINEMINSUM | Sum of pine-dominated plantations and thinning forests on mineral soil | PINEPLAMIN + PINETHIMIN |
| 32 | ROADSUM | Sum of the length of all types of roads | MAINROAD + REGHIGHWAY + CONNROAD + FORROAD |
| NNDAMAGE | An average number of damage per year in neighboring cells | ||
2.5 Zero-inflated negative binomial modelling
The number of non-damage grid cells (zero cells) in the 1 km2 and 25 km2 cell sizes were excessive in both study areas (52–96% of the cells) indicating zero-inflated data (McCullagh and Nelder 1989). Also, the mean number of damage per grid cell, i.e. the number of compensated damage was smaller than the variance for all cell sizes, which makes our data possibly overdispersed (McCullagh and Nelder 1989). Due to these two factors, we assumed the data to fulfil a zero-inflated negative binomial distribution (ZINB) when modelling the occurrence (binary response, compensated damage occurs or not in a grid cell) and the number of moose damage (Zuur et al. 2009). Out of all 10 km grid cells the number of moose damage cells were higher than non-damage cells in both study areas, but to preserve the comparability of the models among cell sizes we used a ZINB-based modelling procedure also for 10 km cells. However, we also constructed models with exactly the same variable combinations for the number of damage by using a negative binomial (NB) distribution, and compared the performance of the ZINB and NB models using a Vuong test (Vuong 1989).
Zero-inflated count models are two-component mixture models in which the distribution of counts is represented by two separate components: the zero component models the probability of false zeros and a count component models true zeros and non-zero values (Zuur et al. 2009). Count models that use zero-inflated negative binomial (ZINB) distribution assume that zeros can come from both the binomial process and the count processes. Basically, our data can contain zero (non-damage) grid cells for at least two reasons. First, so-called false zeros (Martin et al. 2005) might occur because a land owner had not applied for compensation, even though moose damage had occurred in the grid cell. Second, zero cells can also be so-called true zeros when there is no moose damage in a grid cell, even though it contains plantations susceptible to damage. Therefore, the probability (Pr) that there is no moose damage Y in a cell i, can be written as
Pr(Yi = 0) = Pr(False zeros) + (1 – Pr(False zeros)) × Pr(Count process gives a zero).
In ZINB regression, the response variable Yi (i = 1,…n) has a probability mass function, i.e. the observation is zero or non-zero, given by:
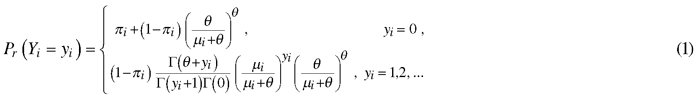
where πi is the logistic link function with regressors z1…zn and 0≤ πi ≤ 1, µi is the mean of negative binomial distribution with regressors x1…xn and µ ≥ 0, θ is the dispersion parameter with θ > 0and Γ(.) is the gamma function. The logistic regression with logit link function is given by:
log it(πi) = eα + β1z1 + β2z2 + … + βnzn .
The quantities in negative binomial distribution modelled with regression can be written as:
µi = α + β1x1i + β2x2i + βkxki ,
where α is an intercept and β1, β2, … βk are unknown parameters for regressors (landscape variables) x that are estimated from data.
Zero-inflated models use binomial general linear models (GLM) to model the probabilities of measuring zeros, and the count process is modelled by a Poisson, or as in our case, negative binomial distribution (Zuur et al. 2009). The idea of ZINB modelling is to first estimate the zero part of the model with a binary model, and after that, to calculate estimates for the count part of the model. The probability for a zero to belong to either of the groups is taken into account when modelling count part of the model. As a result, two models are produced. The first that gives the best combination of variables for predicting zero-cases, i.e. non-damage grid cells in our data. The second model gives variables that best predict the number of damage as a function of the variables.
Grid cells that are adjacent or close to each other are likely to have more similar characteristics in terms of moose damage and landscape characteristics than more distant ones and are thus spatially correlated. To account for spatial autocorrelation we used a simple autocovariate model (Dormann et al. 2007) by calculating the mean number of moose damage plantations per year in adjacent grid cells, NNDAMAGE, for each grid cell and forced NNDAMAGE to model as an explanatory variable at each step.
The modelling was made using R and package pscl for zero-inflated negative binomial and binomial modelling and a Vuong test (Zeileis et al. 2008). We used R-package MASS (Venables and Ripley 2002) for calculating a 95% confidence interval for predictions. In calculating confidence intervals, we assumed a normal distribution and used 2500 replicates/random samples for each estimate per unit. Finally, because we only modelled main effects, we also calculated marginal effects of variables and produced graphs of the predicted number of moose damage for the variables included in the final models by using 25%, 50% and 75% quartile levels for the main co-variables in the models. Due to highly skewed distributions, 90 or 95% quantile levels were used for some variables. In this study, we only present model outputs for plantations, because moose damage mostly occurs in these. For zero models we only present models calculated with the mean values of each significant variable estimates.
2.6 Modelling strategy
The total of 32 landscape and road variables (Tables 1a,b) that were calculated for each grid cell yield numerous plausible variable combinations and, consequently, too many candidate models to be all tested. In addition, not all the variable combinations are interesting or relevant with respect to the study question. Therefore, we formed ten models (later referred as Model #1, Model#2, ...Model#10) consisting of different combinations of variables (Table 2). Variables that were used in modelling consist of either one or more original landscape variables or the sums of these.
| Table 2. Model steps and the effect of different landscape features on moose damage that were tested in each step. At each step, models were constructed as many times as was necessary to find a combination of only significant variables in both the count and zero models. A final model was constructed by entering all significant variables from each step to the same model and by finding variable combinations with the lowest AIC and where all variables in the both count and zero models were significant. At each step, also the average number of damage in neighboring cells (NNDAMAGE) was forced to both the count and zero models. | |||
| Model step, unit | Original variables in model | Hypothesized effect on damage risk | Reference |
| #1, % | FORESTSUM | Sum of all types of forests | (Michaud et al. 2014) |
| #2, % | FORESTSUM and MANMADESUM | Effect of forests and man-made habitats | (Frid and Dill 2002; Michaud et al. 2014) |
| #3, % | OPENMIN, OPENPEAT, PLANTSUM, THINNSUM and MATURE | Effect of open habitats and forest development classes in forestry land | (Cederlund and Okarma 1988; Cassing et al. 2006; Olsson et al. 2011) |
| #4, % | PINEPLANTSUM, OTHERPLANT, PINETHINNSUM and OTHERTHI | Effect of tree species in plantations and thinning forests | (Bjørneraas et al., 2011; Bergqvist et al., 2014) |
| #5, % | PINEPLAMIN, PINEPLANTPEATSUM, PINETHIMIN and PINETHINNPEATSUM | Effect of soil type in pine dominated younger forest development classes | (Heikkilä et al. 1996; Olsson et al. 2011) |
| #6, % | PINEMINSUM and PINEPEATSUM | Effect of soil type in pine dominated younger forest development classes | (Heikkilä et al. 1996) |
| #7, % | PINEPLAPEATDR, PINEPLAPEATND, PINETHIPEATDR and PINETHIPEATND | Effect of drainage in pine dominated plantations and thinning forests on peatlands | (Heikkilä and Härkönen 1993) |
| #8, % | PINEDRSUM and PINENDSUM | Effect of drainage in pine dominated younger development classes on peatlands | (Heikkilä and Härkönen 1993) |
| #9, %, km | INHABITED, AGRI, MANMADE and ROADSUM | Effect of different types of man-modified areas | (Herfindal et al. 2009; Bjørneraas et al. 2011) |
| #10, km | MAINROAD, REGROAD, CONNROAD and FORROAD | Effect of road types | (Ball and Dahlgren 2002; Beyer et al. 2013) |
Models were formed in an essentially hierarchical manner, where Model#1 consists of two variables, forest (sum of the proportion of all forests) and non-forest (sum of the proportion of all non-forest areas), and Model#2 of forests and human-modified land (sum of all human modified area). For Model#3, only forest variables were used and forests were divided according to forest age into five classes. For Model#4, young forests were divided according to their age into plantations and thinning forests but also according to the dominance of pine, yielding a total of four variables. For Model#5 pine-dominated young forests were divided according to soil type (4 variables). For model#6, all pine-dominated young forests were divided into peatland and mineral soil forests (2 variables). For Model#7, young peatland forests were divided into drained and non-drained peatland forests (4 variables). In Model#8, all young pine-dominated forests were divided into either drained or non-drained forests (2 variables). In Model#9, the proportions of different types of human-modified non-forest land were used in the modelling (4 variables). In Model#10, we included the length of the different road classes in model (4 variables).
At each step we ran the models as many times as necessary to find only significant variables in both the count and zero models. Finally, we included all the significant variables from Models #1–10 in a final model and calculated estimates for the model as many times as needed to obtain only significant variables in both the zero and count models. We used Akaike´s information criteria (AIC) for model comparisons in each model step and to select the best combination of variables in the models. Models with ∆AIC > 2 were considered to be significantly different (Burnham and Anderson 2002).
3 Results
3.1 Differences among models
Both in Ostrobothnia and Lapland and for all the landscape sizes, several model combinations with significant variables in both count and zero models could be constructed. As judged by ∆AIC, there were, however, large differences among models because the ∆AIC values were more than 10 units, in most cases tens of units and the largest ∆AIC was 276.16 (Suppl. files S3 and S4). Comparison of ZINB and NB models with the Vuong test indicated that ZINB models were better than NB models for all the models. The number of moose damage per year in neighbouring grid cells, NNDAMAGE, was also a significant predictor in all the models constructed and in both the count and zero parts of the models (showing opposite signs of the estimate, though). Therefore, when discussing significant variables in the models below, we focus only on variables other than the number of moose damage in neighboring grid cells.
3.2 Ostrobothnia 1 km2
In the final count model for Ostrobothnia 1 km2 landscapes, pine-dominated plantations on mineral soil, non-pine-dominated plantations, thinning forests, mature forests and inhabited areas were the best predictors (Table 3). In the zero model increasing proportion of mature forests reduced the probability for non-damage cells (Table 3, Suppl. file S5).
| Table 3. Coefficients, standard error of mean, Z-test value, and significance of the best combination of model variables explaining the amount of moose damage (count model) and the occurrence of a non-damage landscape (zero model) in Ostrobothnia for 1 km2, 25 km2 and 100 km2 landscape sizes. See Tables 1a,b for variable descriptions. | ||||||||||
| Landscape size | Count model | Coeff | Std. Error | Z | Pr(>|z|) | Zero model | Coeff | Std. Error | Z | Pr(>|z|) |
| 1 km2 | Intercept | –3.020 | 0.2074 | –14.557 | <0.0001 | Intercept | 2.9666 | 0.1940 | 15.29 | <0.0001 |
| PINEPLAMIN | 0.0251 | 0.0089 | 2.8 | 0.0051 | MATURE | –0.0177 | 0.0039 | –4.533 | <0.0001 | |
| OTHERPLANT | 0.0715 | 0.0073 | 9.748 | <0.0001 | NNDAMAGE | –11.5357 | 1.1283 | –10.224 | <0.0001 | |
| THINNSUM | 0.0283 | 0.0045 | 6.204 | <0.0001 | ||||||
| MATURE | 0.0156 | 0.0023 | 6.661 | <0.0001 | ||||||
| INHABITED | –0.1121 | 0.0310 | –3.61 | 0.0003 | ||||||
| NNDAMAGE | 0.6801 | 0.0567 | 11.991 | <0.0001 | ||||||
| Log(theta) | –0.5132 | 0.0786 | –6.525 | <0.0001 | ||||||
| 25 km2 | Intercept | –1.7445 | 0.4615 | –3.78 | 0.0001 | Intercept | 3.8015 | 0.7310 | 5.2 | <0.0001 |
| INHABITED | –0.0535 | 0.0265 | –2.018 | 0.0435 | THINNSUM | –0.0605 | 0.0241 | –2.505 | 0.0122 | |
| PLANTSUM | 0.0650 | 0.0113 | 5.75 | <0.0001 | MATURE | –0.0415 | 0.0105 | –3.948 | <0.0001 | |
| MATURE | 0.0331 | 0.0063 | 5.194 | <0.0001 | NNDAMAGE | –0.7188 | 0.1045 | –6.877 | <0.0001 | |
| NNDAMAGE | 0.1396 | 0.0146 | 9.518 | <0.0001 | ||||||
| Log(theta) | 0.2535 | 0.1154 | 2.196 | 0.0281 | ||||||
| 100 km2 | Intercept | –2.0130 | 0.6761 | –2.977 | 0.00291 | Intercept | 10.6547 | 3.3201 | 3.209 | 0.00133 |
| PLANTSUM | 0.0931 | 0.0177 | 5.24 | <0.0001 | OPENMIN | –7.0583 | 3.1600 | –2.234 | 0.02551 | |
| MATURE | 0.0458 | 0.0106 | 4.32 | <0.0001 | MATURE | –0.2559 | 0.0793 | –3.224 | 0.00126 | |
| NNDAMAGE | 0.0649 | 0.0094 | 6.853 | <0.0001 | NNDAMAGE | –0.21 | 0.1237 | –1.697 | 0.08967 | |
| Log(theta) | –0.0676 | 0.1221 | –0.554 | 0.57988 | ||||||
The predicted number of damage exceeded the average number of damage in the actual data already at very low proportions of both mature forests and thinning forests (data not shown). A similar effect was found for pine-dominated plantations on mineral soil when the proportion of non-pine-dominated plantations was used as a covariate (data not shown). When different proportions of non-pine-dominated plantations were used as covariates their effects on the predicted number of damage as a function of pine-dominated plantations were rather mild. Instead, the negative effect of inhabited areas on the number of damage predicted with non-pine-dominated plantations is clear and the predicted number of damage decreases by factor 0.125 when the proportion of inhabited areas increases from 1.6% to 7.1%, i.e., from one damage per 178 ha to one damage per 1428 ha (Fig. 2). For pine-dominated plantations on mineral soil, the decrease in the number of damage was by a factor of 0.166, i.e., from one damage per 178 ha and to one damage per 1071 ha. However, the model overestimates the number of damage for Q25 and Q50, therefore, the data is not shown.
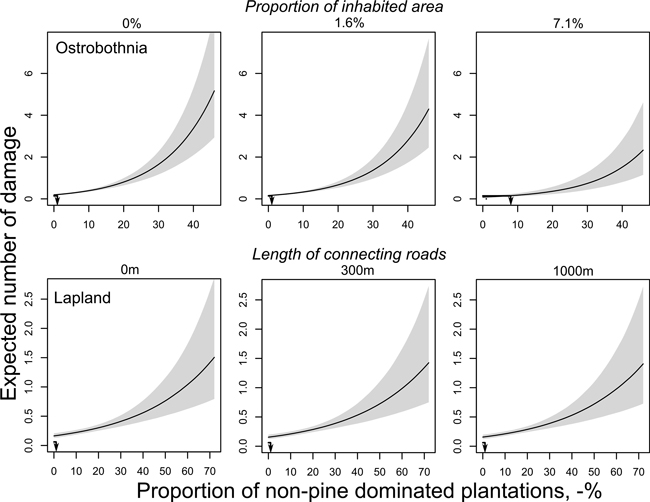
Fig. 2. Predicted number of moose damage per 1 km2 landscape size in relation to the proportion of non-pine-dominated plantations and different proportions of inhabited areas in Ostrobothnia (upper row) and the length of connecting roads in Lapland (lower row). Predictions were calculated for different proportions of non-pine-dominated plantations by using Q1 (left column), Q2 (middle column) and 90% quartile (right column) for the proportion of inhabited area and length of roads while keeping all other possible covariates at their means. Arrow lines show the average number of damaged plantations during years 2002–2008 (Y-axis) and change in moose damage risk per plantation area (X-axis) as a function of different levels of co-variates. Grey area shows 95% confidence limits.
3.3 Ostrobothnia 25 km2
The proportion of all plantations, mature forests and inhabited areas were the best predictors for the count model and for the Ostrobothnia 25 km2 landscapes (Table 3). The probability for zero damage cells decreased with increasing proportions of thinning and mature forests (Table 3, Suppl. file S5).
The predicted number of damage as a function of the sum of all plantations increased by factor 1.6 when the proportion of mature forests increased from 30.5% to 47.9% (Fig. 3). In practice, this means that where there is an average of one damage per 195 ha of plantations with 30.5% mature forests the model predicts one damage per 120 ha plantations when the proportion of mature forests is 47.9%. Instead, an increase in inhabited areas decreased the number of damage by factor 0.8 when the proportion of inhabited areas increased from 0.2% to 5%, i.e. the model predicted one damage per 153 ha and 186 ha plantations, respectively (Fig. 3).
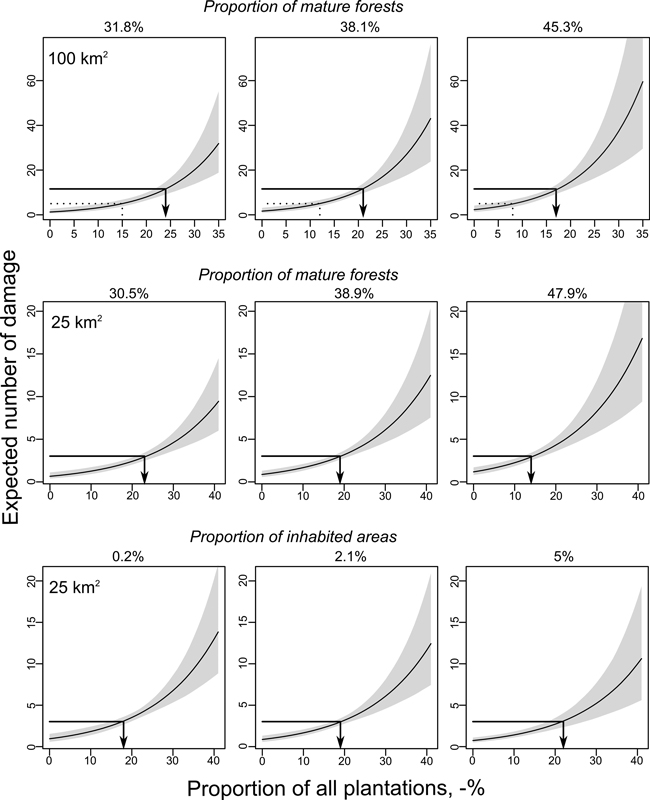
Fig. 3. Predicted number of moose damage per 100 km2 and 25 km2 landscape sizes in Ostrobothnia. Predictions were calculated for different proportions of plantations using quartiles of Q1 (left column), Q2 (middle column) and Q3 (right column) for the proportion of mature forests and inhabited areas while keeping all other possible covariates at their means. However, due to the highly skewed distribution 95% was used for inhabited areas as the highest value. Arrow lines show the average number of damaged plantations in Ostrobothnia during years 2002–2008 (Y-axis) and the change in moose damage risk per plantation area (X-axis) as a function of different levels of co-variates. Grey area shows 95% confidence limits.
3.4 Ostrobothnia 100 km2
The proportion of all plantations and mature forests were the best predictors for the count model for 100 km2 landscapes in Ostrobothnia (Table 3). For the zero model, mature forests and open land in mineral soils were the best predictors and an increase in both variables decreased the probability of finding a non-damage grid cell (Suppl. file S5). However, due to very large confidence intervals the proportion of open land on mineral soils did not yield feasible predictions (data not shown).
The number of predicted moose damage increased by factor 1.4 when the proportion of mature forests increased from 31.8% to 45.3% (Fig. 3), i.e. one damage per 211 ha and 151 ha of all plantations were predicted, respectively.
3.5 Lapland 1 km2
Pine plantations on mineral soil, non-pine-dominated plantations and the sum of thinning forests were the best predictors of the number of damage for 1 km2 landscapes in Lapland (Table 4). The increasing length of connecting roads also showed a negative effect on the number of moose damage. For the zero model, open areas on minerals soils, non-pine-dominated plantations, the sum of thinning forests and mature forests predicted that the probability of finding a non-damage grid cell decreases as the proportions of these variables increase (Table 4, Suppl. file S6). Marginal effect plots of the count models showed that for both the proportion of pine plantations on mineral soils and for the proportion of non-pine-dominated plantations on all soils the models predict two to three times more damage than shown on average in the actual data (data not shown). The effect of connecting roads had a negative effect on the predicted number of damage (Fig. 2) but, as with other covariates, the model predictions were about two-fold compared with actual data.
| Table 4. Coefficients, standard error of mean, Z-test value, and significance of the best combination of model variables explaining the amount of moose damage (count model) and the occurrence of non-damage landscape (zero model) in Lapland for 1 km2, 25 km2 and 100 km2 landscape sizes. See Tables 1a,b for variable descriptions. | ||||||||||
| Landscape size | Count model | Coeff | Std. Error | Z | Pr(>|z|) | Zero model | Coeff | Std. Error | Z | Pr(>|z|) |
| 1 km2 | Intercept | –2.2366 | 0.2040 | –10.96 | <0.0001 | Intercept | 5.0515 | 0.3698 | 13.657 | <0.0001 |
| PINEPLAMIN | 0.0162 | 0.0047 | 3.4 | 0.0006 | OPENMIN | –0.0834 | 0.0237 | –3.508 | 0.0004 | |
| OTHERPLANT | 0.0305 | 0.0055 | 5.482 | <0.0001 | OTHERPLANT | –0.0572 | 0.0101 | –5.64 | <0.0001 | |
| THINNSUM | 0.0090 | 0.0048 | 1.861 | 0.0627 | MATURE | –0.0347 | 0.0058 | –5.924 | <0.0001 | |
| CONNROAD | –0.3729 | 0.1089 | –3.424 | 0.0006 | THINNSUM | –0.0233 | 0.0083 | –2.798 | 0.0051 | |
| NNDAMAGE | 0.9644 | 0.1189 | 8.106 | <0.0001 | NNDAMAGE | –20.0562 | 1.9089 | –10.507 | <0.0001 | |
| Log(theta) | –1.1670 | 0.0861 | –13.554 | <0.0001 | ||||||
| 25 km2 | Intercept | –1.4960 | 0.5314 | –2.815 | 0.0048 | Intercept | 2.7071 | 0.3673 | 7.37 | <0.0001 |
| PLANTSUM | 0.0435 | 0.0096 | 4.515 | <0.0001 | PINEPLAMIN | –0.0478 | 0.0209 | –2.289 | 0.0221 | |
| CONNROAD | –0.0323 | 0.0149 | –2.172 | 0.0298 | OTHERTHI | –0.0883 | 0.0211 | –4.173 | <0.0001 | |
| PINETHIMIN | –0.0255 | 0.0123 | –2.068 | 0.0386 | NNDAMAGE | –1.2680 | 0.2660 | –4.766 | <0.0001 | |
| MATURE | 0.0418 | 0.0103 | 4.038 | <0.0001 | ||||||
| NNDAMAGE | 0.2226 | 0.0314 | 7.081 | <0.0001 | ||||||
| Log(theta) | –0.157 | 0.1588 | –0.988 | 0.3230 | ||||||
| 100 km2 | Intercept | –2.1043 | 0.8740 | –2.408 | 0.0160 | Intercept | 5.29983 | 1.5867 | 3.34 | 0.0008 |
| PLANTSUM | 0.06123 | 0.0169 | 3.609 | 0.0003 | PLANTSUM | –0.09539 | 0.0352 | –2.704 | 0.0068 | |
| MATURE | 0.06606 | 0.0172 | 3.831 | 0.00018 | FORROAD | –0.04346 | 0.0224 | –1.934 | 0.0531 | |
| NNDAMAGE | 0.09991 | 0.0181 | 5.495 | <0.0001 | NNDAMAGE | –0.74811 | 0.1965 | –3.806 | 0.0001 | |
| Log(theta) | 0.00511 | 0.1732 | 0.03 | 0.9764 | ||||||
Zero models either predicted a non-damage grid cell to be found with very high proportions of variables or they had confidence levels up to 60–70% indicating that the model performance was not very good for any of the variables (Suppl. file S6).
3.6 Lapland 25 km2
The sum of all plantations together, thinning forests on minerals soil, and mature forests best explained the number of moose damage in 25 km2 landscapes in Lapland (Table 4). The occurrence of non-damage grid cells was best explained by the proportion of pine plantations on mineral soils and non-pine-dominated thinning forests (Suppl. file S6).
According to the mean model, the predicted number of damage as a function of the proportion of all plantations showed a rather slow increase until the proportion reached about 40–50 % of the 25 km2 landscape (Fig. 4). However, the 95% confidence intervals start to grow substantially at the same point. The predicted number of damage increased along with increasing proportion of mature forests (Fig. 4). When the proportion of mature forests increased from 12.8% to 25.4% the number of damage was predicted to increase by factor 1.5, i.e. from one damage per 630 ha to one damage per 407 ha, respectively. An increase in pine-dominated thinning forests, instead, reduced the predicted number of damage by factor 0.86, i.e. from one damage per 463 ha plantations to one damage per 537 ha plantations. Similarly, an increase in connecting roads from 1.9 km to 8.1 km reduced the predicted number of damage by factor 0.83, i.e. from one damage per 463 ha to one damage per 537 ha (Fig. 4).
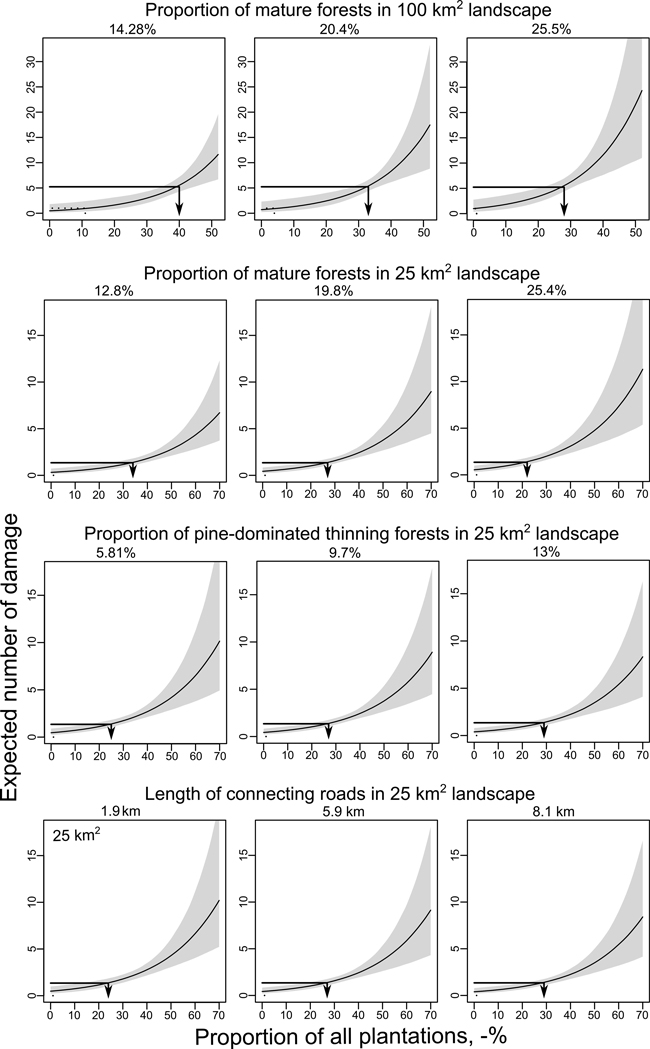
Fig. 4. Predicted number of moose damage per 100 km2 and 25 km2 landscape sizes in Lapland. Predictions were calculated for different proportions of plantations using quartiles of Q1 (left column), Q2 (middle column) and Q3 (right column) for the proportions of mature forests and thinning forests and for the length of connecting roads while keeping all other possible covariates at their means. Arrow lines show the average number of damaged plantations in Lapland during years 2002–2008 (Y-axis) and the change in moose damage risk per plantation area (X-axis) as a function of different levels of co-variates. Grey area shows 95% confidence limits.
3.7 Lapland 100 km2
The sum of all plantations and mature forests were the only significant predictors for 100 km2 landscape count model in Lapland (Table 4). The number of moose damage increased along with increasing percentage of both variables. The sum of all plantations and the length of forest roads predicted that the probability of non-damage grid cells decreases when the proportions of these variables increase. However, for both variables 95% confidence levels were large, up to ±73% of the mean, indicating poor model performance (Suppl. file S6).
The mean model showed that the predicted number of damage increases slowly as a function of all plantations until the proportion of plantations is about 40–50 % of the landscape (Fig. 4). At the same time, however, the 95% confidence levels of the predicted damage also increase strongly. An increase in mature forests from 14.3% to 25.5% increased the predicted number of damage per plantation areal unit by a factor of 1.4, i.e. from one damage per 191 ha to one damage per 134 ha.
4 Discussion
4.1 Mature forests
According to our models “Mature forest” was a significant variable in five out of six final count models and in four out of six zero models. An increase in the proportion of mature forests increased the number of damage in all models and decreased the probability of no moose damage in a grid cell. Our results are in accordance with Olsson et al. (2011) and Bjørneraas et al. (2011), who found that moose home ranges included more mature forests than generally found in landscapes. In winter, mature forests do not provide much forage for moose, but they might provide better cover and, perhaps, lower energy costs due to lower snow depth or the structure of the snow (Bjørneraas et al. 2011).
The effect of mature forests on moose browsing risk might also be related to landscape structure in terms of grain size (Cassing et al. 2006). The average size of regeneration area in privately owned forests in Finland is 1–2 hectares (source Finnish Forestry Centre). Over time, regeneration areas become embedded in the mosaic of forests of different successional stages. Due to small overall compartment size, the distance between cover (mature forest) and food resource (plantations) is rather short, especially when related to the home range size of moose. In Fennoscandia there is no evidence of the effect of patch size on the intensity of browsing in different parts of plantations (Andren and Angelstam 1993), which might imply that due to increased cover-food adjacencies moose might perceive forestry modified landscapes as fine grained. In fine grained-landscapes moose browsing is more evenly distributed than in landscape with large variation in patch size (Edenius et al. 2002).
In our study areas mature forest is the most common habitat type out of all original habitat types studied, at just under 40% in Ostrobothnia and about 20% in Lapland, and thus the probability of finding mature forest in a grid cell is higher than all other habitat types. It should be remembered, however, that according to our habitat classification mature forests included all forests that had >81 m3 ha–1 of total volume of trees (Table 1) and thus our forest class “Mature forests” category includes not only old-growth forests, sensu stricto, but also advanced thinning forests. According to definition (Metsäntutkimuslaitos 2002) advanced thinning forests comprise some timber-sized trees and, in our study areas, these forests were 40–60 years old.
4.2 Thinning forests
The effect of thinning forests on the number of damage varied according to scale and type of thinning forests. In the 1 km2 models, an increase in all thinning forests predicted the number of damage to increase in both Ostrobothnia and Lapland. The mechanisms behind this are probably the same as for mature forests; thinning forests do not provide much food in winter but they might provide better cover and lower energy costs due to lower snow depth or the structure of the snow (Bjørneraas et al. 2011). Furthermore, the food-cover adjacencies might have the same effect in thinning forest plantation mosaics as mature forests.
In the 25 km2 model in Lapland, the number of damage decreased when the proportion of pine-dominated thinning forests increased, although a post hoc analysis showed a significant positive correlation between the proportion of pine-dominated thinning forests and pine-dominated plantations (Spearman’s rho = 0.685, p < 0.001). One plausible explanation would be the legacy of post WWII forestry in Lapland, when large forest areas were clear cut and regenerated mainly with Scots pine. Deciduous trees are a common admixture in plantations regenerated for pine and cleaning and soil scarification are used to reduce competing vegetation in plantations. In the least productive sites plantations also develop more or less as pine-dominated monocultures throughout the rotation period. Dense pine-dominated thinning forests thus provide only a limited amount of browse for moose in winter. Therefore, moose probably do not favour areas dominated by pine-dominated thinning forests but establish their winter ranges in areas with a more diverse mosaic of forests comprising other species in addition to pine.
4.3 Inhabited areas and roads
According to our 1 km2 and 25 km2 Ostrobothnia models, the number of moose damage decreased as the amount of inhabited areas increased. The effect was clear especially when the number of damage was predicted as a function of pine-dominated plantations on mineral soils and inhabited areas were used as a covariate. In general, the average proportion of inhabited areas in our data was rather low, from 1.6% to 2.1%, depending on the grid cell size (Suppl. file S1). However, the proportion of inhabited areas was on average two to six times higher in no-damage grid cells than in damage grid cells, the highest difference being in 1 km2 grid cells. The difference between damage grid cells and the overall landscape was marginally smaller, but still about the same magnitude (Suppl. file S1). There were similar differences in Lapland, although inhabited area was not a significant variable in any of the models.
Although moose can exploit variations in food and cover caused by human land use (Bjørneraas et al. 2011), the vicinity of inhabited areas and human activities causes a trade-off in habitat use (Lykkja et al. 2009). In addition to avoidance of areas close to human habitation (Tinoco Torres et al. 2011), the time during which moose are most active, e.g. browsing, might also be shorter in areas close to human habitation as compared with more remote areas (Lykkja et al. 2009). In this sense, the response of moose to human disturbance has been suggested to be analogous to the response to predator risk (Frid and Dill 2002), according to which human disturbance can induce predator avoidance behaviour and cause animals to shift their habitats farther from the disturbance source. According to this hypothesis, one pre-requisition for habitat shift is that there are available habitats for foraging also farther from inhabited areas. Since WWII, forestry has strongly changed the structure of the forest landscape in Finland in terms of the amount and pattern of different age classes, and has especially increased the amount of young successional stages. Therefore, moving farther from inhabited areas is unlikely to lower the probability of moose finding good quality habitats also in there.
Our finding regarding the effect of roads on damage risk is in line with some earlier studies that suggest that the vicinity of roads decreases damage risk (Repo and Löyttyniemi 1985). However, Ball and Dahlgren (2002) found that major highways might increase moose damage close to roads by inhibiting moose from migrating across roads and by increasing moose density near to roads. According to our findings, the effect of roads was the opposite; the higher the length of connecting roads, the less damage incurred in 1 km2 and 25 km2 landscapes in Lapland. One explanation for the discrepancy between these findings might be that roads in our study area do not generally form barriers for moose to cross. Ball and Dahlgren (2002) did not attribute the barrier effect to the presence of roadside fences, but rather to the open area formed by major highways. In Lapland, connecting roads, the most common road type after forest roads, are 4–5 m wide and generally asphalted. Moose vehicle collisions occur more frequently on connecting roads than any other class of road in Lapland (Finnish Transport Agency 2014), which indicates that connecting roads are not barriers for moose. However, according to our results connecting roads do seem to have an inhibitive effect on moose damage at a distance of up to 2.5–3.5 km from the road. This, again, could be explained by the predator risk hypothesis (Frid and Dill 2002).
4.4 Plantations
The number of damage as a function of the proportion of plantations increased quite slowly until the proportion of plantations was about 18% in Ostrobothnia and about 32% in Lapland, which correspond to average landscapes in both areas, respectively. However, at the same time, the uncertainty of the predictions starts to increase strongly, probably due to fewer observations with a high proportion of plantations. The amount of any type of plantations or the total amount of plantations were not good predictors alone for the number of damage. Instead, the number of damage increases when the landscape forms a mosaic of plantations and mature forests or thinning forests. This is in line with (Bjørneraas et al. 2012; Herfindal et al. 2015) who found moose to select areas with habitat types that provide both good forage and cover.
4.5 Transferring models between regions
Our results partly support the idea that the transfer of habitat selection models from one area to another should be made with care (Mabille et al. 2012). Our study areas, Lapland and Ostrobothnia differed from each other in several aspects. In Ostrobothnia, there were more drained peatlands, mature forests, inhabited areas and agricultural land than in Lapland. Instead, there were more regeneration areas, plantations and young thinning forests in Lapland. The road network is also denser and there are more inhabited areas in Ostrobothnia than in Lapland. However, the variables in the models for respective landscape sizes were quite similar for the two areas, indicating that moose damage risk is related to similar habitat composition in both areas. Some differences, like the effect of inhabited areas, roads and pine-dominated thinning forests, still imply that moose damage risk models should include landscape features typical to each region.
4.6 Count models and zero models
There is empirical evidence that the abundance of moose can to some degree be predicted on the basis of predicted occurrence and by partly using the same environmental covariates used in both occurrence and abundance models (Nielsen et al. 2005). If this holds true also for moose damage, data of moose damage and the location of damage in relation to available habitats might be used in predicting the number of damage on the basis of damage probability. However, Michaud et al. (2014) found that the same indicators were ineffective in concurrently predicting both the occurrence and abundance of moose. According to our models, only a few variables explained both the number of damage and the occurrence of damage. It should be remembered that zero models describe conditions where moose damage was not recorded, not conditions where damage was found. Our data results from several mechanisms that can lead to non-damage grid cells and some non-damage grid cells can be so-called false zeros (Martin et al. 2005), i.e. moose damage are present but not recorded. The simplest explanations for this are that existing damage have not been observed, or that damage has been observed but no damage compensation has been sought by the land-owners. Due to the large number of compensated damage spanning several years, we believe, however, that our data are sufficient to describe at least the variation in relative occurrence of damage in our study area.
4.7 General model performance and evaluation
As our modelling shows, it is possible to construct numerous models with reasonable variables and with several variable combinations (Suppl. files S3 and S4). However, when arranged by their AIC, some models are tens or even hundreds of times more informative than others. We do not claim that those models with variables that were not included in the final models are necessarily not useful or uninformative, but instead denote the view of Burnham and Anderson (2002) who regarded model construction as a process of testing several options rather than building the most parsimonious model. Our results do, however, urge careful consideration of the results in relation to the type of landscape/habitat data used in modelling.
Habitat models might perform poorly if habitat selection for a species is strongly density dependent and there is no information available about the population size in relation to long-term cycles or carrying capacity (Boyce et al. 2016). For moose in Finland, information on estimated population size after hunting is available only at the game management area level at scales of 102–104 km2 (Nygrén and Pesonen 1993), while estimates for smaller areas are missing. In winter, moose tend to aggregate to certain winter pastures which means that population densities can be very high and damage can be the result of several individuals. Although studies in Fennoscandia have no found correlation between population density and damage level (Hörnberg 2001b) or density-dependent habitat selection (Månsson 2009), high densities of moose can locally lead to the utilization of sub-optimal habitats. This, again, might level out the effect of varying habitat structure on the amount of browsing.
Finally, our study was based on only one measure of landscape structure: composition of habitats. There is evidence that other indices of landscape structure, like such as patch size, are also linked to browsing intensity (Cassing et al. 2006). Therefore, using other measures of landscape structure, such as mean patch size, distance to other similar patches, patch density and length of edges, as explanatory variables in modelling might provide further insight into moose damage risk in a mosaic landscape (Cassing et al. 2006). Additional variables not measured in this study might also improve the performance of the models at the smallest scale. Furthermore, resources at landscape and region levels might vary due to biogeographical variation, topography or land use (Michaud et al. 2014; Nikula 2017), which should be assessed when evaluating moose damage risk.
Acknowledgements
We thank numerous people at Finnish Forest Centre for gathering and delivering us moose damage data at various stages of this study. We also thank the staff of National Forest Inventory at Natural Resources Institute Finland for proving forest data at our disposal. We also thank two anonymous referees for their constructive comments that helped us to improve the manuscript. This study was partly funded by the grant from the Ministry of Agriculture and Forestry for the project “Big data in management of moose populations and damage”.
References
Ahti T., Hämet-Ahti L., Jalas J. (1968). Vegetation zones and their sections in northwestern Europe. Annales Botanici Fennici 5: 169–211.
Andrén H., Angelstam P. (1993). Moose browsing on Scots pine in relation to stand size and distance to forest edge. Journal of Applied Ecology 30(1): 133–142. https://doi.org/10.2307/2404277.
Ball J.P., Dahlgren J. (2002). Browsing damage on pine (Pinus sylvestris and P. contorta) by a migrating moose (Alces alces) population in winter: relation to habitat composition and road barriers. Scandinavian Journal of Forest Research 17(5): 427–435. https://doi.org/10.1080/028275802320435441.
Ball J.P., Nordengren C., Wallin K. (2001). Partial migration by large ungulates: characteristics of seasonal moose Alces alces ranges in northern Sweden. Wildlife Biology 7(3): 39–47. https://doi.org/10.2981/wlb.2001.007.
Bergqvist G., Bergström R., Edenius L. (2001). Patterns of stem damage by moose (Alces alces) in young Pinus sylvestris stands in Sweden. Scandinavian Journal of Forest Research 16(4): 363–370. https://doi.org/10.1080/02827580119307.
Bergqvist G., Bergström R., Wallgren M. (2014). Recent browsing damage by moose on Scots pine, birch and aspen in young commercial forests – effects of forage availability, moose population density and site productivity. Silva Fennica 48(1) article 1077. https://doi.org/10.14214/sf.1077.
Bergström R., Hjeljord O. (1987). Moose and vegetation interactions in northwestern Europe and Poland. Swedish Wildlife Research Supplements 1: 213–228.
Beyer H.L., Ung R., Murray D.L., Fortin M. (2013). Functional responses, seasonal variation and thresholds in behavioural responses of moose to road density. Journal of Applied Ecology 50(2): 286–294. https://doi.org/10.1111/1365-2664.12042.
Bjørneraas K., Solberg E.J., Herfindal I., Moorter B.V., Rolandsen C.M., Tremblay J., Skarpe C., Sæther B., Eriksen R., Astrup R. (2011). Moose Alces alces habitat use at multiple temporal scales in a human-altered landscape. Wildlife Biology 17(1): 44–54. https://doi.org/10.2981/10-073.
Bjørneraas K., Herfindal I., Solberg E., Sæther B., Van Moorter B., Rolandsen C. (2012). Habitat quality influences population distribution, individual space use and functional responses in habitat selection by a large herbivore. Oecologia 168(1): 231–243. https://doi.org/10.1007/s00442-011-2072-3.
Boyce M.S., Johnson C.J., Merrill E.H., Nielsen S.E., Solberg E.J., van Moorter B. (2016). Can habitat selection predict abundance? Journal of Animal Ecology 85(1): 11–20. https://doi.org/10.1111/1365-2656.12359.
Burnham K.P., Anderson D.R. (2002). Model selection and multimodel inference – a practical information-theoretic approach. Second edition. Springer-Verlag, New York, Inc. 488 p.
Cassing G., Greenberg L.A., Mikusiñski G. (2006). Moose (Alces alces) browsing in young forest stands in central Sweden: a multiscale perspective. Scandinavian Journal of Forest Research 21(3): 221–230. https://doi.org/10.1080/02827580600673535.
Cederlund G., Okarma H. (1988). Home range and habitat use of adult female moose. Journal of Wildlife Management 52(2): 336–343. https://doi.org/10.2307/3801246.
Cederlund G., Sand H. (1994). Home-range size in relation to age and sex in moose. Journal of Mammalogy 75(4): 1005–1012. https://doi.org/10.2307/1382483.
Cederlund G., Ljungqvist H., Markgren G., Ståhlfelt F. (1980). Foods of moose and roe deer at Grimsö in central Sweden. Results of rumen content analyses. Swedish Wildlife Research Viltrevy 11: 169–247.
Dormann C.F., McPherson J.M., Araújo M.B., Bivand R., Bolliger J., Carl G., Davies R.G., Hirzel A., Jetz W., Kissling W.D., Kühn I., Ohlemüller R., Peres-Neto P.R., Reineking B., Schröder B., Schurr F.M., Wilson R. (2007). Methods to account for spatial autocorrelation in the analysis of species distributional data: a review. Ecography 30(5): 609–628. https://doi.org/10.1111/j.2007.0906-7590.05171.x.
Edenius L., Bergman M., Ericsson G., Danell K. (2002). The role of moose as a disturbance factor in managed boreal forests. Silva Fennica 36(1): 57–67. https://doi.org/10.14214/sf.550.
Environmental Systems Research Institute (ESRI) (2012). ArcGIS Release 10.1. Environmental Systems Research Institute, Redlands, CA.
Finlex (2014). Legislation of Finland: game animal damages act. http://www.finlex.fi/fi/laki/kaannokset/2009/en20090105.pdf. [Cited 1 Dec 2014].
Finnish Statistical Yearbook of Forestry (2011). Metsäntutkimuslaitos, Vantaa. Vammalan kirjapaino Oy, Sastamala. 472 p. http://urn.fi/URN:ISBN:978-951-40-2329-3.
Finnish Transport Agency (2014). Hirvieläinonnettomuudet maanteillä 2013. English summary: Elk and deer accidents on highways in 2013. Research reports of the Finnish Transport Agency 6/2014. 23 p.
Frid A., Dill L.M. (2002). Human-caused disturbance stimuli as a form of predation risk. Ecology and Society 6(1). 16 p. http://www.consecol.org/vol6/iss1/art11/. [Cited 15 Nov 2016].
Heikkilä R., Härkönen S. (1993). Moose (Alces alces L.) browsing in young Scots pine stands in relation to the characteristics of their winter habitats. Silva Fennica 27(2): 127–143. https://doi.org/10.14214/sf.a15667.
Heikkilä R., Nygrén K., Härkönen S., Mykkänen A. (1996). Characteristics of habitats used by a female moose in the managed forest area. Acta Theriologica 41(3): 321–326. https://doi.org/10.4098/AT.arch.96-30.
Herfindal I., Tremblay J., Hansen B.B., Solberg E.J., Heim M., Sæther B. (2009). Scale dependency and functional response in moose habitat selection. Ecography 32(5): 849–859. https://doi.org/10.1111/j.1600-0587.2009.05783.x.
Herfindal I., Tremblay J., Hester A.J., Lande U.S., Wam H.K. (2015). Associational relationships at multiple spatial scales affect forest damage by moose. Forest Ecology and Management 348: 97–107. https://doi.org/10.1016/j.foreco.2015.03.045.
Hörnberg S. (2001a). The relationship between moose (Alces alces) browsing utilisation and the occurrence of different forage species in Sweden. Forest Ecology and Management 149(1–3): 91–102. https://doi.org/10.1016/S0378-1127(00)00547-8.
Hörnberg S. (2001b). Changes in population density of moose (Alces alces) and damage to forests in Sweden. Forest Ecology and Management 149 (1–3): 141–151. https://doi.org/10.1016/S0378-1127(00)00551-X.
Korhonen K.T., Ihalainen A., Miina J., Saksa T., Viiri H. (2010). Metsänuudistamisen tila Suomessa VMI10:n aineistojen perusteella. [The state of forest regeneration in Finland according to National Forest Inventory 10]. Metsätieteen aikakauskirja 4/2010: 425–478. https://doi.org/10.14214/ma.6943.
Lavsund S. (1987). Moose relationships to forestry in Finland, Norway and Sweden. Swedish Wildlife Research, Supplement 1: 229–244.
Lavsund S., Nygrén T., Solberg E.J. (2003). Status of moose populations and challenges to moose management in Fennoscandia. Alces 39: 109–130.
Lykkja O.N., Solberg E.J., Herfindal I., Wright J., Rolandsen C.M., Hanssen M.G. (2009). The effects of human activity on summer habitat use by moose. Alces 45: 109–124.
Mabille G., Dussault C., Ouellet J., Laurian C. (2012). Linking trade-offs in habitat selection with the occurrence of functional responses for moose living in two nearby study areas. Oecologia 170(4): 965–977. https://doi.org/10.1007/s00442-012-2382-0.
Månsson J. (2009). Environmental variation and moose Alces alces density as determinants of spatio-temporal heterogeneity in browsing. Ecography 32(4): 601–612. https://doi.org/10.1111/j.1600-0587.2009.05713.x.
Månsson J., Kalén C., Kjellander P., Andrén H., Smith H. (2007). Quantitative estimates of tree species selectivity by moose (Alces alces) in a forest landscape. Scandinavian Journal of Forest Research 22(5): 407–414. https://doi.org/10.1080/02827580701515023.
Månsson J., Andrén H., Sand H. (2011). Can pellet counts be used to accurately describe winter habitat selection by moose Alces alces? European Journal of Wildlife Research 57(5): 1017–1023. https://doi.org/10.1007/s10344-011-0512-3.
Martin T.G., Wintle B.A., Rhodes J.R., Kuhnert P.M., Field S.A., Low-Choy S.J., Tyre A.J., Possingham H.P. (2005). Zero tolerance ecology: improving ecological inference by modelling the source of zero observations. Ecology Letters 8(11): 1235–1246. https://doi.org/10.1111/j.1461-0248.2005.00826.x.
McCullagh P., Nelder J.A. (1989). Generalized Linear Models. Chapman and Hall, London. 511 p. https://doi.org/10.1007/978-1-4899-3242-6.
McGarigal K., Marks B.J. (1995). Fragstats: spatial pattern analysis program for quantifying landscape structure. US Department of Agriculture, Forest Service, Pacific Northwest Research Station, Portland, OR. General Technical Report, PNW-GTR-351. 122 p. https://doi.org/10.2737/PNW-GTR-351.
Metsäntutkimuslaitos (2002). Valtakunnan Metsien 9. Inventointi (VMI9). Maastotyön ohjeet 2002. Kuusamo ja Lappi. [9th National Forest Inventory (NFI9). Field work manual 2002. Kuusamo and Lapland]. 178 p.
Michaud J., Coops N.C., Andrew M.E., Wulder M.A., Brown G.S., Rickbeil G.J.M. (2014). Estimating moose (Alces alces) occurrence and abundance from remotely derived environmental indicators. Remote Sensing of Environment 152: 190–201. https://doi.org/10.1016/j.rse.2014.06.005.
Nielsen S.E., Johnson C.J., Heard D.C., Boyce M.S. (2005). Can models of presence-absence be used to scale abundance? Two case studies considering extremes in life history. Ecography 28(2): 197–208. https://doi.org/10.1111/j.0906-7590.2005.04002.x.
Nikula A. (2017). Resource selection of moose Alces alces at multiple scales – from trees, plantations and home ranges up to landscapes and regions. Dissertationes Forestales 233. 54 p. https://doi.org/10.14214/df.233.
Nikula A., Heikkinen S., Helle E. (2004). Habitat selection of adult moose Alces alces at two spatial scales in central Finland. Wildlife Biology10(1): 121–135. https://doi.org/10.2981/wlb.2004.017.
Nygrén T., Pesonen M. (1993). The moose population (Alces alces L.) and methods of moose management in Finland, 1975–89. Finnish Game Research 48: 46–53.
Ojala A.E.K., Palmu J.-P., Åberg A., Åberg S., Virkki H. (2013). Development of an ancient shoreline database to reconstruct the Litorina Sea maximum extension and the highest shoreline of the Baltic Sea basin in Finland. Bulletin of the Geological Society of Finland 85: 127–144. https://doi.org/10.17741/bgsf/85.2.002.
Olsson M., Cox J.J., Larkin J.L., Widén P., Olovsson A. (2011). Space and habitat use of moose in southwestern Sweden. European Journal of Wildlife Research 57(2): 241–249. https://doi.org/10.1007/s10344-010-0418-5.
Pirinen P., Simola H., Aalto J., Kaukoranta J.-P., Karlsson P., Ruuhela R. (2012). Climatological statistics of Finland 1981–2010. Reports 2012:1. 96 p.
Repo S., Löyttyniemi K. (1985). Lähiympäristön vaikutus männyn viljelytaimikon hirvituhoalttiuteen. Summary: The effect of immediate environment on moose (Alces alces) damage in young Scots pine plantations. Folia Forestalia 626. 14 p. http://urn.fi/URN:ISBN:951-40-0706-9.
Sweanor P.Y., Sandegren F. (1988). Migratory behavior of related moose. Holarctic Ecology 11(3): 190–193. https://doi.org/10.1111/j.1600-0587.1988.tb00800.x.
Sweanor P.Y., Sandegren F. (1989). Winter-range philopatry of seasonally migratory moose. Journal of Applied Ecology 26(1): 25–33. https://doi.org/10.2307/2403648.
Swedish Statistical Yearbook of Forestry (2013.) Skogsstyrelsen. Swedish Forest Agency. 374 p. ISBN 978-91-87535-01-7.
Tinoco Torres R., Carvalho J.C., Panzacchi M., Linnell J.D.C., Fonseca C. (2011). Comparative use of forest habitats by roe deer and moose in a human-modified landscape in southeastern Norway during winter. Ecological Research 26: 781–789. https://doi.org/10.1007/s11284-011-0837-0.
Tomppo E., Katila M., Moilanen J., Mäkelä H., Peräsaari J. (1998). Kunnittaiset metsävaratiedot 1990–1994. [Forest resources by municipalities in 1990–1994]. Metsätieteen aikakauskirja 4B/1998: 619–839. https://doi.org/10.14214/ma.6453.
Tomppo E., Olsson H., Ståhl G., Nilsson M., Hagner O., Katila M. (2008). Combining national forest inventory field plots and remote sensing data for forest databases. Remote Sensing of Environment 112(5): 1982–1999. https://doi.org/10.1016/j.rse.2007.03.032.
Venables W.N., Ripley B.D. (2002). Modern applied statistics with S. Springer. 495 p. https://doi.org/10.1007/978-0-387-21706-2.
Vuong Q.H. (1989). Likelihood ratio tests for model selection and non-nested hypothesis. Econometrica 57(2): 307–333. https://doi.org/10.2307/1912557.
Wallgren M., Bergquist J., Bergström R., Eriksson S. (2014). Effects of timing, duration, and intensity of simulated browsing on Scots pine growth and stem quality. Scandinavian Journal of Forest Research 29(8): 734–746. https://doi.org/10.1080/02827581.2014.960896.
Zeileis A., Kleiber C., Jackman S. (2008). Regression models for count data in R. Journal of Statistical Software 27(8). 25 p. https://doi.org/10.18637/jss.v027.i08.
Zuur A.F., Ieno E.N., Walker N.J., Saveliev A.A., Smith G.M. (2009). Mixed effect models and extensions in ecology with R. Spring Science and Business Media, New York, NY. 574 p. https://doi.org/10.1007/978-0-387-87458-6.
Total of 61 references.

