Evaluating the neighborhood, hybrid and reversion search techniques of a simulated annealing algorithm in solving forest spatial harvest scheduling problems
Dong L., Bettinger P., Liu Z., Qin H., Zhao Y. (2016). Evaluating the neighborhood, hybrid and reversion search techniques of a simulated annealing algorithm in solving forest spatial harvest scheduling problems. Silva Fennica vol. 50 no. 4 article id 1622. https://doi.org/10.14214/sf.1622
Highlights
- The performances of neighborhood, hybrid and reversion search strategies of simulated annealing were evaluated when implemented with a forest spatial harvest scheduling problem
- The performances of alternative search strategies of simulated annealing were all systematic and clear better than the conventional strategy
- The reversion techniques were significant superior to the other search strategies in solving forest spatial harvest scheduling problems.
Abstract
Heuristic techniques have been increasingly used to address the complex forest planning problems over the last few decades. However, heuristics only can provide acceptable solutions to difficult problems, rather than guarantee that the optimal solution will be located. The strategies of neighborhood, hybrid and reversion search processes have been proved to be effective in improving the quality of heuristic results, as suggested recently in the literature. The overall aims of this paper were therefore to systematically evaluate the performances of these enhanced techniques when implemented with a simulated annealing algorithm. Five enhanced techniques were developed using different strategies for generating candidate solutions. These were then compared to the conventional search strategy that employed 1-opt moves (Strategy 1) alone. The five search strategies are classified into three categories: i) neighborhood search techniques that only used the change version of 2-opt moves (Strategy 2); ii) self-hybrid search techniques that oscillate between 1-opt moves and the change version of 2-opt moves (Strategy 3), or the exchange version of 2-opt moves (Strategy 4); iii) reversion search techniques that utilize 1-opt moves and the change version of 2-opt moves (Strategy 5) or the exchange version of 2-opt moves (Strategy 6). We found that the performances of all the enhanced search techniques of simulated annealing were systematic and often clear better than conventional search strategy, however the required computational time was significantly increased. For a minimization planning problem, Strategy 6 produced the lowest mean objective function values, which were less than 1% of the means developed using conventional search strategy. Although Strategy 6 performed very well, the other search strategies should not be neglected because they also have the potential to produce high-quality solutions.
Keywords
spatial harvest scheduling;
metaheuristics;
combinatorial optimization;
neighborhood search;
reversion search
- Dong, Department of Forest Management, College of Forestry, Northeast Forestry University, Harbin 150040, China E-mail farrell0503@126.com
- Bettinger, Warnell School of Forestry and Natural Resources, University of Georgia, Athens 30602, GA, USA E-mail pbettinger@warnell.uga.edu
-
Liu,
Department of Forest Management, College of Forestry, Northeast Forestry University, Harbin 150040, China
E-mail
lzg19700602@163.com

- Qin, Department of Forestry Economic, College of Economic & Management, Northeast Forestry University, Harbin 150040, China E-mail huiyanqin@hotmail.com
- Zhao, Department of Forest Management, College of Forestry, Northeast Forestry University, Harbin 150040, China E-mail zyinghui0925@126.com
Received 25 April 2016 Accepted 17 August 2016 Published 1 September 2016
Views 132974
Available at https://doi.org/10.14214/sf.1622 | Download PDF

1 Introduction
Forest management planning processes often provide detailed guidance to forest managers concerning where, when, and how management prescriptions should be scheduled across a landscape. However, broader concerns related to the environment (e.g., wildlife habitat, biodiversity, carbon sequestration), and in response to new demands from society, have contributed to planning problems becoming increasingly complex and sophisticated. Advancements in harvest scheduling have shown that traditional mathematical programming techniques (e.g., mixed integer programming) can be exploited to produce feasible forest management plans that accommodate harvest adjacency and green-up requirements (McDill et al. 2002; Tóth et al. 2013). However, depending on how these problems are formulated, some substantive limitations may arise when the planning techniques are applied to large forests (Bettinger et al. 2015). Therefore, heuristic techniques have increasingly been assessed for their potential use in the development of large, complex forest management plans. The most common reason for using heuristic techniques instead of mathematical techniques may be the need to incorporate complex spatial objectives into the planning problems formulation that are not easily represented by linear or non-linear equations, but rather by computer programming logic (as in Bettinger et al. 1997). For example, heuristic techniques have been applied to forestry planning problems that involve the maximization of economic and commodity production objectives (Boston and Bettinger 1999; Crowe and Nelson 2005; Strimbu et al. 2010), the maintenance and development of wildlife habitat (Hof and Flather 1996; Kurttila et al. 2006; Marshalek et al. 2014), the maintenance of forest stand-level structure (Tang et al. 2004; Bettinger et al. 2007), the issues related to carbon sequestration of a forest (Hernandez et al. 2014; Pukkala 2014), the issues concerning fragmentation of a forested landscape (Kurttila et al. 2002; Bettinger et al. 2007), and the impact of management activities on water quality (Bettinger et al. 1998; Fotakis 2015). Numerous examples of the use of heuristics for solving complex combinatorial problems from fields outside of forestry can also be found in the literature (Los and Lardinois 1982; Fuller et al. 2012; Sinclair et al. 2014; Arikan et al. 2016).
Heuristic techniques usually can be classified into s-metaheuristic (or point-based) methods, where improvements are made to single solution per iteration, or p-metaheuristic (or population-based) methods, where improvements are made to a population of solutions (or a subset) per iteration. The s-metaheuristics, such as simulated annealing (Metropolis et al. 1953; Öhman and Lämås 2003; Borges et al. 2014a, 2014b) and tabu search (Richards and Gunn 2000; Bettinger et al. 2007), typically only maintain one solution per iteration of the search process, and often it represents a feasible solution. These heuristics utilize intensification and diversification search strategies to modify the solution in an attempt to locate the global optimum; these processes can further assist in escaping local optima. However, p-metaheuristics, such as genetic algorithms (Lu and Eriksson 2000) and particle swarm optimization (Shan et al. 2012), maintain a set of feasible solutions per iteration. With these heuristics, strategies are employed to improve the entire population (or sub-set) of solutions so that a broad area of the solution space might be explored simultaneously. Within the field of forestry, s-metaheuristic techniques have been widely used in forest planning problems, perhaps because they involve more intuitive processes than p-metaheuristics techniques. More importantly, some studies have suggested that p-metaheuristics techniques may be less effective in solving complex forest spatial planning problems when the harvest adjacency restrictions are integrated (Bettinger et al. 2002; Liu et al. 2006), but this conclusion highly depends on the actual implementation of the heuristic methods, and how solutions are modified to allow the population to evolve. For example, Bettinger et al. (2002) and Liu et al. (2006) reported that genetic algorithms were not appropriate when applied to a strict harvest adjacency problem due to the large number of constraint violations incurred, but when limited genetic information is passed from parents to child solutions, few constraint violations can occur. Further, others have found more promising results when applying p-metaheuristics to spatial forest planning problems (Pukkala and Kurttila 2005).
Well-developed heuristic methods only can guarantee that high-quality, feasible solutions to complicated problems can be located within a reasonable amount of computer processing time. This does not imply that the global optimal solution can also be located. Therefore, previous researchers have put forward some ideas for improving the quality and robustness of solutions generated by heuristic techniques. These ideas can be classified into three categories: 1) neighborhood search techniques, 2) hybrid metaheuristic methods, and 3) reversion search methods. Depending on the number of the status (i.e., management prescription or harvest periods) of stands are changed simultaneously during each iteration of an s-metaheuristic model, the search process can be considered as 1-opt, 2-opt or n-opt moves, respectively. For forest management problems, the performance of 2-opt moves have been shown to be superior to the use of 1-opt moves alone. For example, Bettinger et al. (1999), and Caro et al. (2003), and Heinonen and Pukkala (2004) reported that the strategy of 2-opt moves could significantly improve the quality of heuristic solutions (or forest plans). However, 2-opt moves might be ineffective when the planning problem is very large, due to the amount of time required to assess the value of the potential change and to assess the resulting constraints (Bachmatiuk et al. 2015).
Hybrid search techniques may also be of value in locating higher quality heuristic solutions to planning problems because they can utilize the different search behaviors of heuristic methods. The potential performance of hybrid search techniques has been illustrated in a number of forest planning papers. For example, Boston and Bettinger (2002) suggested that a hybrid tabu search/generic algorithm may lead to a 2% increase in objective function values when compared to the standard implementation of tabu search. Li et al. (2010) also examined several hybrid models that involved simulated annealing, threshold accepting, tabu search and the raindrop method (Zhu and Bettinger 2006), and found that more than 75% of the solutions generated by hybrid models were of higher quality than solutions generated by standard implementations of basic heuristic algorithms. In addition, Bettinger et al. (2002, 2007) introduced an unparalleled search strategy that combined 1-opt and 2-opt moves together, which could be considered as self-hybrid process. Very recently, Bettinger et al. (2015) noted that search reversion may also dramatically improve s-metaheuristic results by interrupting the sequence of search process events, and re-initiating the search process from a high-quality solution value. However, the performance of this strategy needs to be assessed on a wider scale and scope of planning problem.
The above mentioned alternative search techniques of heuristics have previously been illustrated in some forestry literature, however few previous research efforts have been made to compare the performances of these techniques. Therefore, the overall aims of this article are to evaluate the performances of neighborhood search techniques, hybrid search techniques, and reversion search techniques when applied to a large forest spatial harvest scheduling problem, using a simulated annealing algorithm. The objective function of the planning problem used in this analysis is to minimize the deviations from an assigned harvest volume target. A unique strategy is associated with the policy constraints, in which the final harvest (clear-cutting) prescription should comply with the unit restriction model (URM) of adjacency constraints. However the spatial and temporal assignment of three different intensities of selective cutting prescriptions should comply with the area restriction model (ARM) of adjacency constraints. Finally, the stated problems are applied to a large and real forest landscape in northeast China.
2 Materials and methods
2.1 Data description
The study area we apply to evaluate the performance of three enhanced search techniques is a 123 293 ha forest in northeastern China (52°41´N, 123°51´E). The elevations of this area varied from 230 to 1397 m. The mean annual precipitation is approximately 428 mm, mainly concentrating on July and August within each year. The mean annual temperature is approximately –2.4 °C, and length of snow cover is as long as five months, namely from October to March. The soil in this area is dominated by dark-brown coniferous forest soil, with a few amounts of meadow soil and boggy soil. The forest area contains 325 compartments, which were divided into 6421 subcompartments (or management units). The landscape can be classified into five forest types: 1) natural Larix gmelinii forests (NLG); 2) natural Betula platyphylla forests (NBP); 3) coniferous mixed forests (CF); 4) broad-leaved mixed forests (BF); and 5) coniferous and broad-leaved mixed forests (CBF). In this classification, the five forest types account for 30.67%, 14.39%, 27.96%, 19.90% and 2.73% of the total area, respectively. In addition, approximately 4.36% area can be considered as non-forest land. Details about the forest dataset can be found from Dong et al. (2015). The age class distribution of the study area is illustrated in Fig. 1. The potential management prescriptions for each management unit (Table 1), which mainly depended on the stand age, were devised to satisfy the requirements of the laws and regulations on forest management from the Heilongjiang Province in northeast China (State Development Planning Commission and State Forestry Bureau 2010).
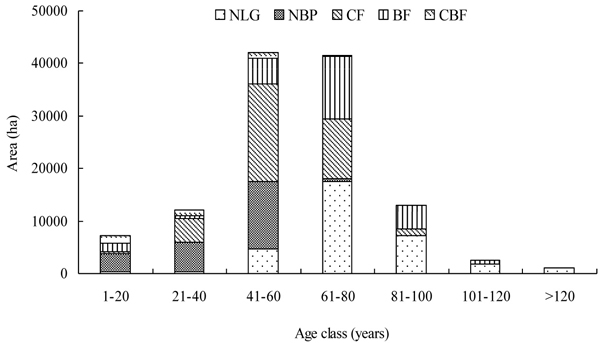
Fig. 1. The age class distribution of forest landscape dataset, where NLG = natural Larix gmelinii dominated forests, NBP = natural Betula platyphylla dominated forests, CF = coniferous forests, BF = broad-leaved forests, and CBF = coniferous and broad-leaved mixed forests.
| Table 1. The potential management prescriptions for the forest planning problems. | ||||
| No. | Management prescription | Limit age (year) | Description | |
| Broad-leaved forest a | Coniferous forest b | |||
| 0 | No harvest | < 20 | < 30 | Strictly prohibit any management prescriptions when stand age is less than the limiting ages |
| 1 | Mild selective cutting c | 21–50 | 31–80 | Only can adopt one of the three intensities of selective cutting, as well as no harvest, when stand age ranges within the interval of the limiting ages |
| 2 | Moderate selective cutting d | |||
| 3 | Severe selective cutting e | |||
| 4 | Final harvest | > 50 | > 80 | Can adopt final harvest, selective cutting and no harvest when forest age is more than the limiting ages |
| a include natural Betula platyphylla dominated forests (NBP) and broad-leaved forests (BF) b include natural Larix gmelinii dominated forests (NLG), coniferous forests (CF) and coniferous and broad-leaved mixed forests (CBF) c the intensity of selective cutting was assumed as 10% of the total volume for a management unit d the intensity of selective cutting was assumed as 20% of the total volume for a management unit e the intensity of selective cutting was assumed as 30% of the total volume for a management unit | ||||
2.2 Forest planning problem formulation
The forest plans that we investigated cover ten 1-yr planning periods. The objective function of the forest planning problem involves minimizing the squared deviation between the scheduled harvest volume in each time period and a static target harvest volume. This objective is analogous to the tactical plan and the objective function found in Bettinger et al. (2007, 2015).

Here, T is the total number of planning periods, t is a planning period (one year), and target_volume is a user-specified desired harvest volume to be scheduled during each planning period. The target volume was assumed to be 50 000 m3 per period (year) consistent, which was retrieved from the policy of forest cutting quota of local government during the 12th Five-Years Plan (2011–2015). Ht is the scheduled harvest volume in time period t. Since the deviations between the scheduled and desired harvest volumes are squared, the units for the objective function were (m3)2 in this research. To determine the scheduled harvest volume during each iteration of the heuristic search process, methods were employed that in effect are consistent with accounting rows used in linear programming problem formulations:

Here, i is an arbitrary management unit, I is the total number of management units, p is a single management prescription, and P is the total number of management prescriptions. Further, xipt is an integer decision variable (i.e., xipt = 0, 1, 2, 3 and 4) indicates whether the stand i was assigned to be harvested with management prescription p during time period t, and vipt is the available harvest volume from unit i when managed under prescription p during time period t.
Three main sets of constraints are employed. One set refers to resource constraints and two sets refer to policy constraints. The resource constraints, also known as the singularity constraints, are used to prevent each management unit from being clearcut harvested more than once during the entire planning horizon:

One set of policy constraints is associated with the selective cutting prescriptions using the ARM constraints and the other set is associated with the final harvest prescription using the URM constraints. Generally speaking, the neighboring units are strictly prohibited to be assigned a final harvest prescription in the same (or near) time period using URM constraints (Murray 1999). However, to further increase the complexity of this problem, the green-up constraints are also integrated into the planning formulations, as implemented in Boston and Bettinger (2002), and Zhu and Bettinger (2008).

Here, the potential management prescription only involves the final harvest (i.e., p = 4); z is a management unit adjacent to unit i; Ui is the set of all adjacent units around unit i; m is a near-time period; Tm represents the set of near-time periods. As Boston and Bettinger (2002) defined, the set of near-time periods (Tm) for a 3-year green-up constraints can be written as: m1 = t–3, m2 = t–2, m3 = t–1, m4 = t, m5 = t + 1, m6 = t + 2 and m7 = t + 3 ( where all mz ≥ 0, otherwise not in Tm; and all mz ≤ T, otherwise not in Tm). xzpt is also an integer decision variable indicating whether management unit z is assigned a final harvest prescription p during near-time period t.
The ARM constraints are employed to restrain the spatial and temporal distributions of selective prescriptions, in which some contiguous management units to be selectively harvested concurrently in the same (or near) time periods are allowed, but the combined area must less than a user-defined maximum size (Murray 1999). The commonly used maximum opening size constraints and maximum average opening size constraints are both integrated into the planning problem. As mentioned above, our ARM constraints also hold for a 3-yr green-up periods. Therefore, the maximum opening size constraints could be presented as:
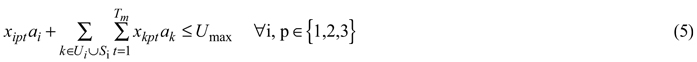
In this case, the management prescriptions are only one of the three intensities of selective cutting or no harvest (i.e., p = 1, 2 or 3), and k is a management unit from a subset of management units adjacent to unit i and the neighbors of management unit i, and so on, in the form of a recursive function (as in Murray 1999). Si is a set of management units adjacent to the neighbors of unit i, ai and az are the areas of management units i and z, respectively, and xkpt is an integer decision variable. The latter variable indicates that management unit k is assigned a selective cutting prescription p during near-time period t. The maximum opening size assumed (Umax) was 90 ha. The maximum average opening size, which is an important forest management practice mainly due to the legal and voluntary restrictions, is also included into the planning formulation.
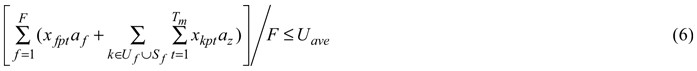
For this, xfpt is an integer decision variable defining the management prescription p assigned to management unit f during the planning period t, af is the area of management unit f, F is the total number of harvesting patches, and Uave is the maximum average opening size assumed, which was assumed in this work to be 30 ha.
2.3 Simulated annealing algorithm
Simulated annealing is a typical heuristic search technique that has been described by others (e.g., Crowe and Nelson 2005; Borges et al. 2014a; Baskent and Jordan 2002; Bettinger et al. 2002) as potentially being of value to many types of forestry problems, such as those with economic and commodity production objectives or those that involve harvest adjacency or wildlife constraints. The crucial characteristic of simulated annealing algorithm is that when searching for an optimal solution, it can conditionally accept inferior solutions, which may allow the search process escape from local optima. This distinct mechanism prompts simulated annealing algorithm to explore other areas of the solution space, thus increasing the probability that it will be able to generate a high quality solution. Simulated annealing was chosen for this work because it has previously been confirmed as being one of the better heuristics for spatial planning problems (Boston and Bettinger 1999; Bettinger et al. 2002; Liu et al. 2006). The general search process of simulated annealing for minimization problems can be described as (Metropolis et al. 1953; Borges et al. 2014a):
 |
Within the flow of this process, s0 is an initial feasible solution, ![]() is a current feasible solution,
is a current feasible solution, ![]() is a new feasible solution,
is a new feasible solution,![]() is the best feasible solution, Tmax is the initial temperature, Tmin is the freezing temperature, Tt is the number of iterations allowed at each temperature, and Tr is the cooling rate. As Pukkala and Heinonen (2006) noted, the performance of heuristics (including simulated annealing) will depend on the search parameters employed. These can affect the search process significantly, thus the values of parameters of heuristics should be carefully considered prior to applying them in a forest planning effort. Since the purpose of this study was to analyze the performance of three different enhanced techniques in solving complex planning problems, rather than optimize the parameters of simulated annealing, the parameters were therefore set to be 10 000 (Tmax), 10 (Tmin), 200 (Tt), and 0.998 (Tr). All parameters were static when used in the tested search strategies in the forthcoming case study. The values of the four parameters were evaluated in a quantitative manner using a trial-and-error test, in a manner similar to what others (Boston and Bettinger 1999) have attempted. In effect, this parameter set should result in 690 200 iterations per independent run, ignoring unsuccessful attempts to make changes to the current solution.
is the best feasible solution, Tmax is the initial temperature, Tmin is the freezing temperature, Tt is the number of iterations allowed at each temperature, and Tr is the cooling rate. As Pukkala and Heinonen (2006) noted, the performance of heuristics (including simulated annealing) will depend on the search parameters employed. These can affect the search process significantly, thus the values of parameters of heuristics should be carefully considered prior to applying them in a forest planning effort. Since the purpose of this study was to analyze the performance of three different enhanced techniques in solving complex planning problems, rather than optimize the parameters of simulated annealing, the parameters were therefore set to be 10 000 (Tmax), 10 (Tmin), 200 (Tt), and 0.998 (Tr). All parameters were static when used in the tested search strategies in the forthcoming case study. The values of the four parameters were evaluated in a quantitative manner using a trial-and-error test, in a manner similar to what others (Boston and Bettinger 1999) have attempted. In effect, this parameter set should result in 690 200 iterations per independent run, ignoring unsuccessful attempts to make changes to the current solution.
The candidate solution of simulated annealing during each iteration is created by firstly randomly selecting a management unit and then randomly selecting a management prescription within the unit. Therefore, the strategies of generating candidate solution may have significant effects on the search process and the quality of heuristic solutions. However, to our best knowledge, few previously works in the literature have compared these strategies used for generating candidate solutions. In this paper, we will attempt to evaluate the usefulness of neighborhood search techniques, hybrid search techniques and reversion search techniques of simulated annealing in solving forest planning problems. In the following sections, we will give a detailed description of these alternative search strategies.
Strategy 1: The first search strategy utilizes the standard version of simulated annealing (i.e., 1-opt moves) to incrementally improve the quality of a forest plan (Fig. 2-A). Exploring the neighborhood of a solution in this strategy can be described as: 1) randomly select a management unit; 2) randomly assign a management prescription or change the harvest period within the unit; 3) evaluate the feasibility of a potential move against the resource and policy constraints; 4) evaluate the acceptability of the potential move with respect to the objective function value. As implemented here, moves that improved the objective function value are always accepted, non-improving moves are accepted by comparing the result of the Boltzman formula (e(–∆E/t)) to a randomly generated number. If the randomly generated number is less than e(–∆E/t), then the inferior move can also be accepted.
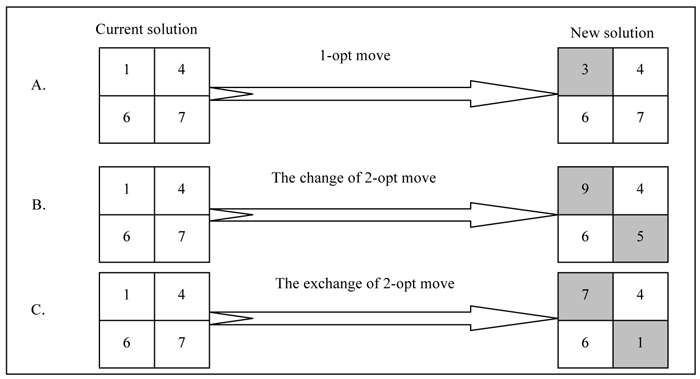
Fig. 2. The schematic diagram of different neighborhood search strategies of simulated annealing, where A is 1-opt moves, B is the change version of 2-opt moves, and C is the exchange version of 2-opt moves. The number in each cell represents the assigned harvest period.
Strategy 2: The second search strategy employs the 2-opt moves that were described in Heinonen and Pukkala (2004) and Bachmatiuk et al. (2015), in which the assigned harvesting period and management prescription of two different units are changed (not exchanged) simultaneously (Fig. 2-B). In this paper, this search strategy will be called the change version of 2-opt moves consistent. The reason for using this strategy is that the search process may get trapped in local optima when the planning problems include strict spatial (i.e, adjacency) and non-spatial (i.e., even-flow of harvest volume) constraints. This strategy might produce a smaller change to the objective function value, and thus it can produce solutions that might not be obtainable using the 1-opt moves. Therefore, the change version of 2-opt moves have been widely used in a set of important forestry planning problems, indicating that it can improve the quality of heuristic solutions significantly when compared that with 1-opt moves (Heinonen and Pukkala 2004; Caro et al. 2003).
Strategy 3: The third search strategy will oscillate back and forth the search process between 1-opt and the change version of 2-opt moves, namely the 2-opt moves in Strategy 2. This strategy can be considered as a self-hybrid heuristic search process. The Strategy 2 has previously been confirmed effective in producing higher-quality solutions, but the computational time could be significantly lengthened. Heinonen and Pukkala (2004), for an example, reported that the computational time of the Strategy 2 (described above) was usually as large as two (or more) times than that of 1-opt moves for the four commonly used heuristic algorithms (i.e., random ascent, Hero, simulated annealing and tabu search) when applied to forest spatial planning problems. The hypothesis of this strategy is that a moderate oscillation between 1-opt and 2-opt moves not only can produce higher quality solutions, but do not increase the computational time significantly. However, the main consideration of this process was how to determine the integration points (as denoted by the iteration number) for oscillating the search process from 1-opt moves to 2-opt moves. We employ a fixed breakpoint method which was introduced by Bettinger et al. (2015), in which an integration point can be calculated as:

where qr is the break point for r-th oscillation; r is the r-th oscillation; R is the total number of oscillations; Q is the total number of iteration of the search process which depend on the four parameters of simulated annealing. Therefore, the oscillation process may occur at some points depending on the state of iteration counter. As an example, if the total number of iterations for an independent run is 100, and the number of oscillation is 4, then after 25th, 50th, 75th iteration, oscillation occurs. In the following oscillation (or reversion) strategies, the fixed break point method will be employed constantly, and a set of oscillation (or reversion) intervals (i.e., R = 2, 4, 6, 8, 10) are also evaluated to detect whether they have significant effects on the objective function value.
Strategy 4: The fourth search strategy, similar to Strategy 3, will also oscillate back and forth the search process between 1-opt and 2-opt moves, however the assigned harvest period and management prescriptions between two different units are exchanged (i.e., not simply changed; Fig. 2-C). This is the 2-opt search strategy first described in the forestry literature in Bettinger et al. (1999) and later evaluated in Bettinger et al. (2002, 2007), showing that it is effective for improving the quality of solutions. We define this strategy as self-hybrid metaheuristic process. Obviously, this strategy of 2-opt moves must be employed based on a high quality, feasible initial solution and cannot be implemented in absence of 1-opt moves. Unlike the 2-opt moves in Strategy 2, the exchange management prescriptions fine-tunes the quality of the solution by intensifying the search in areas nearby the current solution, and logically might produce a smaller change in the objective function value. The search process will firstly employ a set of 1-opt moves to diversify the search, and then employ a set of 2-opt moves to intensify the search.
Strategy 5: The fifth strategy uses reversion search technique within the search process, as described in Bettinger et al. (2015). The search process first employs a set of 1-opt moves to diversity the search prior to using 2-opt moves that are described in Strategy 2, and then the current solution is replaced with the best solution stored in memory. After the appropriate 2-opt moves are made, the search process returns to 1-opt moves once again. This strategy can take full use the advantages of 2-opt moves and meanwhile intensify the search around high-quality solutions.
Strategy 6: The last strategy, similar to Strategy 5, but uses the 2-opt moves described in Strategy 4. To our knowledge, the direct use of this strategy has received little attention with respect to optimization problems. Two exceptions, Sinclair et al. (2014) employed it to solve an airline scheduling problems, and Bettinger et al. (2015) applied it to solve forest spatial harvest scheduling problems, both of them indicating that this strategy was significant superior to the standard version of heuristics.
2.4 Statistical analysis
There are a number of ways to evaluate the performance of heuristics (see details from Bettinger et al. 2009), however a statistical analysis of the solutions is an important method. Since all candidate solutions of all the six alternative search strategies of simulated annealing were generated randomly, the candidate solutions for different search strategies were logical different. As Golden and Alt (1979) and Los and Lardinois (1982) described, each resulting solution of a heuristic algorithm can be considered as an independent sample from a large population, If the initiation point of the search process was chosen randomly. Therefore, the search process of each strategy was repeated 60 times, and then the objective function values of these solutions were evaluated in two different ways: 1) the statistical values (i.e., mean and standard deviation) of the 60 independent runs for each search strategy were compared quantitatively for the objective function values and the length of computational time as a self-validation process (Bettinger et al. 2009). As implemented here, the length of computational time was defined as the time that the search process located the maximum objective function value for the first time, 2) an ANOVA analysis was employed to detect whether the differences of the objective function values among the six alternative search strategies were significant or not.
3 Results
3.1 The effects of reversion rates
The best solutions (i.e., the minimum objective function values) that were generated using Strategies 3 to 6 with different oscillation (or reversion) rates are illustrated in Table 2. The results showed that the values of the best solution for each search strategy have no pronounced tendency as the oscillation (or reversion) rates increased. An increase in the reversion rate actually allows the search processes to spend more time searching with a current solution prior to reverting back to the best solution stored in memory. We were hopeful that we would be able to notice a trend in the solution values given changes in the reversion rate (i.e., revert less often should either lead to better or worse solutions). The best forest plan was generated using Strategy 6 with a reversion interval of 10 iterations, and the value of this solution was 11.8, which indicated that the scheduled harvest volumes for each time period were extremely near to the target volumes, i.e., the mean deviation between the scheduled and targeted harvest volume was only 0.34 m3 per year (period), which was denoted as ΔV = 0.34 m3/yr. For comparison purposes, all solutions that were generated with other search strategies (i.e., Strategies 3–5) would be compared with this datum value. The objective function value of the best solution for Strategy 3 was 73.2 when the oscillation interval was 6 iterations, which was approximately 6 times as large in value as the best solution from Strategy 6. However, the best solution for Strategy 4 with an oscillation interval of 10 iterations (12.9) and Strategy 5 with a reversion interval of 4 iterations (13.1) were both consistent with that of the best solution from Strategy 6, which were only about 1.09 and 1.11 times than that of the best solution from Strategy 6.
| Table 2. Quality ((m3)2) of the best solutions (i.e., minimum solution values) generated with five different exchange rates (Methods 3 and 4) and reversion rates (Methods 5 and 6) for the forest spatial planning problem, where R2-R10 represent the five oscillation (or reversion) rates (i.e., R = 2, 4, 6, 8, 10). | |||||
| Method | Oscillation / reversion rate | ||||
| 2 | 4 | 6 | 8 | 10 | |
| 3 | 87.6 | 135.7 | 73.2 | 143.2 | 89.7 |
| 4 | 62.0 | 23.3 | 66.9 | 20.9 | 12.9 |
| 5 | 60.0 | 13.1 | 50.8 | 51.7 | 88.5 |
| 6 | 20.9 | 29.2 | 16.0 | 36.2 | 11.8 |
The ANOVA indicated that the oscillation (or reversion) rates usually have some moderate influences on the objective function values (Fig. 3). The mean objection function values of Strategy 3 presented a slight downtrend with the increases of oscillation rates, but the differences among them were not significant. The reason might be that the search strategy would be more similar to the change version of 2-opt moves (i.e., Strategy 2) when the oscillation rates increased significantly. Strategy 4 with an oscillation interval of 2 iterations produced significantly larger mean objective function values than that of other oscillation rates. In addition, Strategy 6 showed similar results with Strategy 4 when evaluated the effects of different reversion rates. However, the differences of the mean objective function values for Strategy 5 between the reversion interval of 2 and 8 iterations were difficult to distinguish, but both of them were significant larger than that of the other three reversion rates.
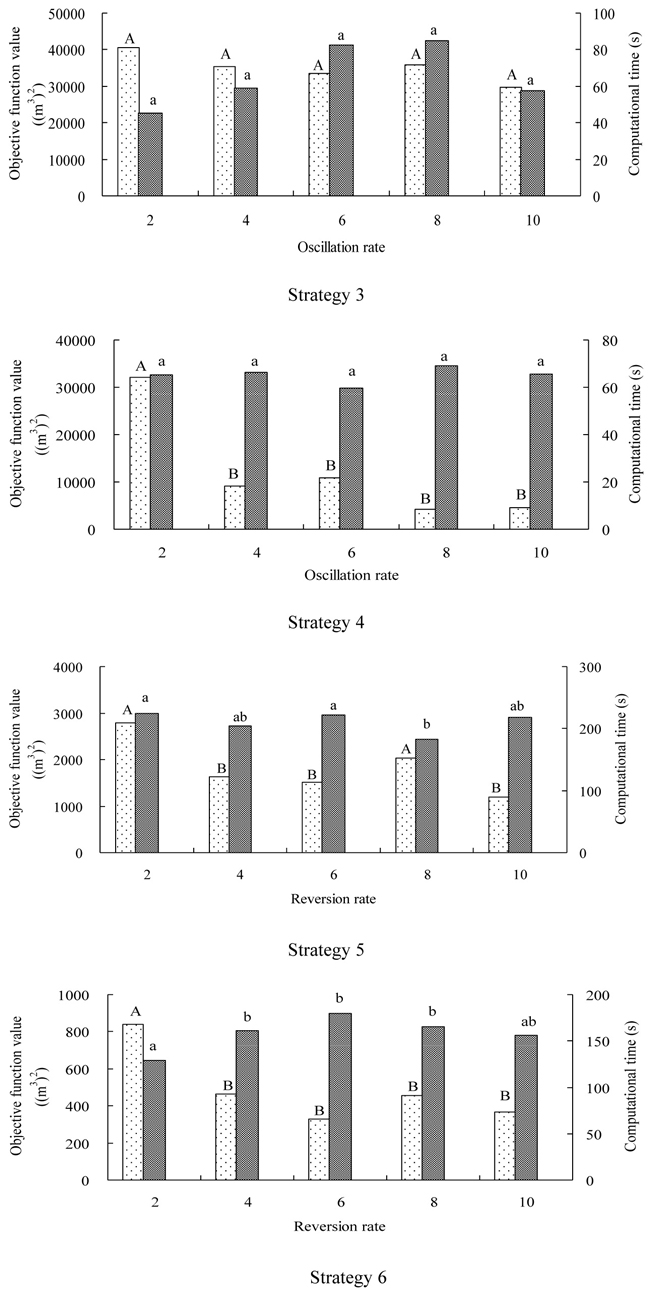
Fig. 3. The mean objective function values (dot-bar) and computational time (line-bar) required for the different oscillation rates (Strategies 3 and 4) and reversion rates (Strategies 5 and 6) for the forest spatial planning problem. The same upper-case letter in the dot-bar indicates that there are no significant differences in objective function values at α = 0.05 between different search strategies when implemented with simulated annealing algorithm. The same lower-case letter in the line-bar indicates that there are no significant differences in computational time at α = 0.05 between different search strategies when implemented with simulated annealing algorithm.
The oscillation (reversion) rates usually had no appreciable impacts on the computational time for Strategies 3 and 4 in our case study, in which the mean computational time of the two search strategies was almost consistent with each other (66 seconds). However, the reversion rates had some indefinable influences on the computational time for Strategy 5 and 6. The mean computational time for Strategy 5 with a reversion interval of 8 iterations (183 seconds) was significant shorter than that when using a reversion interval of 2 or 6 iterations (225 and 222 seconds), but no significant differences were observed when the reversion interval of 4 or 10 iterations (204 and 218 seconds) were employed. For Strategy 6, the computational time for a reversion interval of 2 iterations (129 seconds) was significant shorter than that when using the other reversion rates (161, 180 and 166 seconds), except for the reversion interval of 10 iterations (156 seconds). It appears that the reversion process may influence the computation of the acceptance probabilities using the Boltzman formula. The difference in the proposed and current solutions (revert occasionally to the best solution in memory) may produce probabilities of acceptance that are too small allow inferior solutions to replace current solutions. This may then impact how quickly the process anneals, and thus concludes its search for the best solution.
3.2 The evaluation of different search strategies
The oscillation (or reversion) rates usually had some moderate effects on the objective function values (Fig. 3) as mentioned above, but the functional mechanisms remained unclear, because of the stochastic behavior of simulated annealing. Therefore, we had no choice but to select the optimal oscillation (or reversion) rate for each search strategy just based on the average objective function values without considering the significance of the differences. From the point of this view, the optimal oscillation (or reversion) rates were 10, 8, 10 and 6 iterations for Strategies 3 to 6, respectively. The quality of the 60 independent solutions for each search strategy was presented in Table 3, which provided us some insights into the quality of solutions among different search strategies. Strategy 6 generated the minimum mean solution values (327.3), which indicated that the ΔV was only 1.81 m3/yr. The second and third minimum mean solution values were generated by Strategies 5 and 4, and the values were as large as 3.64 and 12.64 times than that of Strategy 6. As expected, the standard version of simulated annealing (Strategy 1) generated the maximum (worst) mean solution values, which were as large as 111.65 times that of Strategy 6. The ANOVA analysis indicated that there were no significant differences among Strategies 4 to 6 with respect to the mean objective function values, but in fact they were significant superior to other search strategies (i.e., Strategies 1–3). Strategies 2 and 3 also produced significantly different mean objective function values that that of Strategy 1, however no significant differences were observed between Strategies 2 and 3. The variations of the sixty solution values from Strategies 1 to 4 were much larger (more dispersed objective function values) than that of the other two search strategies, indicating a higher stability of the solutions generated using reversion search techniques (Strategies 5 and 6).
| Table 3. The statistical characteristics of objective function values and computational time of 60 independent solutions for the six alternative search strategies when implemented with simulated annealing algorithm. | ||||||||
| Search strategy | Objective function values (m3)2 | Computational time (seconds) | ||||||
| Minimum | Maximum | Mean | Standard deviation | ANOVA groups a | Mean | Standard deviation | ANOVA groups b | |
| 1 | 410.1 | 113 712.0 | 36 541.7 | 26 011.1 | A | 41.1 | 47.1 | a |
| 2 | 29.4 | 78 059.7 | 25 559.3 | 22 544.5 | B | 162.2 | 208.6 | b |
| 3 | 89.7 | 113 668.0 | 29 679.4 | 23 443.0 | B | 57.4 | 82.3 | a |
| 4 | 20.9 | 77 266.0 | 4138.2 | 9864.1 | C | 69.1 | 77.8 | a |
| 5 | 88.5 | 5867.5 | 1190.5 | 1413.1 | C | 218.3 | 89.8 | c |
| 6 | 16.0 | 1346.9 | 327.3 | 291.2 | C | 180.1 | 75.7 | bc |
| a The same letter indicate that there are no significant differences in objective function values at α = 0.05 between different search strategies when implemented with simulated annealing algorithm. b The same letter indicate that there are no significant differences in computational time at α = 0.05 between different search strategies when implemented with simulated annealing algorithm. | ||||||||
The computational time required significantly increased, no matter which kind of 2-opt moves were implemented. Strategy 5 usually required the longest mean computational time to generate acceptable solutions (218.3 seconds), which was about 5.31 times than that of the standard version of simulated annealing (41.1 seconds). The next longest computational time was Strategies 6 and 2 respectively, which required approximately 4.38 and 3.95 times than that of Strategy 1. The computational time required for Strategies 1, 3 and 4 were significant shorter than that of the other three search strategies. The computational time required for Strategy 2 was also significant shorter than that of Strategy 5, however there were no significant differences between Strategy 2 and Strategy 6. The differences between Strategies 5 and 6 were also insignificant.
Fig. 4 illustrated how many, of the sixty independent solutions generated by each search techniques of simulated annealing, were ranged within 10 times of the best values (11.8) generated by Strategy 6 with a reversion interval of 10 iterations. Using this metric, Strategy 6 provided a probability of 25% to generate high quality solutions, which confirmed that it was the most suitable strategy to solve forest spatial harvest scheduling problems. However, the second most suitable strategies (Strategies 2 and 5) could only provide a probability of approximately 8% to generate high quality solutions. The worst strategy, the standard version of simulated annealing (Strategy 1), was confirmed that it may be not convenient for forest spatial harvest scheduling problems given the benefits that the enhancements provided.
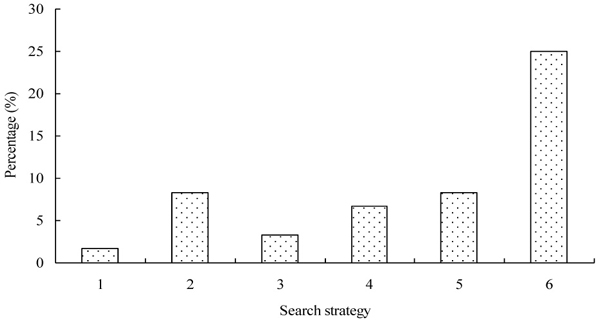
Fig. 4. The percentage of the sixty objective function values for each search strategy that varied within 10 times (i.e., ≤ 118.0 (m3)2) of the best solution value generated by Strategy 6 with a reversion interval of 10 iterations.
The spatial and temporal assignment of management prescriptions of a small subarea of the best solution that were generated by Strategy 6 with a reversion interval of 10 iterations was presented in Fig. 5, where the spatial constraints were rather evident and clearly discernible with the naked eye. The scheduled harvest volumes for each period of the presented plan were exactly nearly what were desired. The best forest plan showed that only 10.89% of the management units were scheduled for cutting with one of the four potential management prescriptions during the entire time horizon. The mild, moderate and severe selective cutting and final harvest prescriptions produced approximately 9.96%, 19.01%, 27.43% and 43.6% of the total harvest volume, and accounted for scheduled activity within 3.43%, 3.18%, 3.11% and 1.17% of the total number of management units.
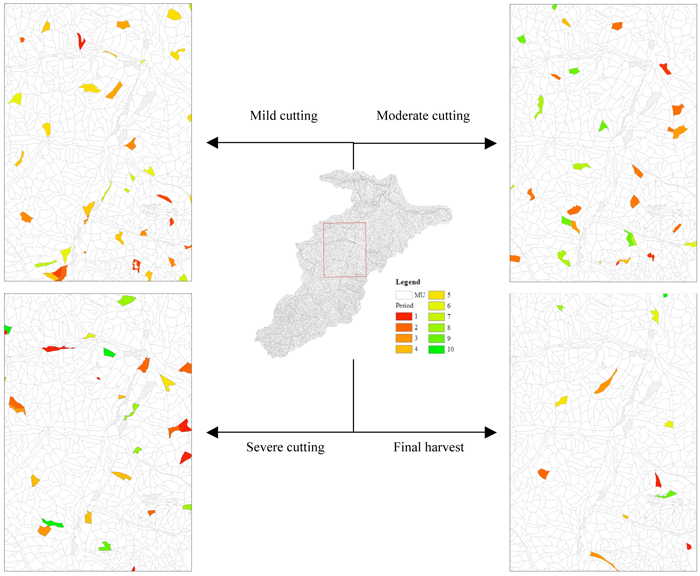
Fig. 5. The spatial and temporal assignment of management prescriptions of a small subarea for the best solution that generated by Strategy 6 with a reversion interval of 10 iterations, where MU is management unit. View larger in new window/tab.
4 Discussion and conclusions
Forest management planning processes are one of the most complex tasks for forest managers and decision-makers, especially when the adjacency constraints of harvest are considered. Therefore, the optimization processes of these planning problems are highly dependent on mathematical programming technology. Simulated annealing, as a heuristic search process, has been widely used to address this type of problems and efforts on improving its performance are also always worthy from scientific perspective. In this paper, we compared the performances of six alternative search strategies in spatial harvest scheduling problem when implemented with a simulated annealing algorithm. In addition to the conventional strategy (Strategy 1) to generate candidate solutions, we examined five enhanced search strategies for generating candidate solutions, in which one referred to the neighborhood search technique (Strategy 2), two referred to self-hybrid search techniques (Strategy 3 and 4) and two referred to reversion techniques (Strategy 5 and 6). The six alternative search strategies of simulated annealing were evaluated on a large and complex forest planning problem. The obtained results showed that the reversion technique (Strategy 6) provided higher-quality solutions than other techniques (Table 3), which confirmed our expectations perfectly. Although the performances of the rest search strategies were not as good as Strategy 6, they should not be neglected since they also have the potential to produce high-quality solutions. Therefore, we can conclude that heuristic algorithms, including simulated annealing, must need some necessary refinements to produce higher quality solutions in practice.
The performance of heuristic algorithm is also highly dependent on the parameters used. However, in order to implement a controlled experiment and to avoid confounding effects of any combination of parameters, the values of the four pivotal simulated annealing parameters were held constant for each search strategy of simulated annealing employed in our research. Based on the work of Boston and Bettinger (1999) and Pukkala and Heinonen (2006) we can conclude that the quality of solutions might be improved sequentially if an optimal combination of these parameters were used. Conducting a sensitivity analysis of parameter values for each search strategy of simulated annealing was always worthy from the perspectives of scientific, however it may be difficult and time-consuming to implement the sensitivity analysis of the four parameters for the tested six search strategies in this paper, thus we have to leave this area of investigation for future research efforts. In addition, the strategy used for selecting management units and treatment schedules to generate candidate solutions also have significant effects on the quality of solutions generated. In our study, we firstly used a uniform probability to select the management unit, and then another two uniform probability distributions were applied to select the time period when the management prescription should occur and the management activity to be applied within the selected management unit. However, Borges et al. (2014a, 2014b) recently reported that solutions could be significantly improved when introducing bias into the probabilities for management unit and treatment prescription selection process when compared to unbiased probabilities (i.e., the standard version of heuristic). However, the biased probabilities for selecting choices should be dynamic rather than static. Therefore, there might exist some potential to produce higher quality solutions from s-metaheuristics by introducing biased probabilities during a s-metaheuristic search process (with the exception of traditionally deterministic processes such as tabu search).
The techniques of oscillating between 1-opt and 2-opt moves can be considered as self-hybrid technique, which has been described by Boston and Bettinger (2001) and Li et al. (2010). Therefore, the decision criteria for deciding when to switch from one search strategy to another might have significant effects on the quality of solutions generated and on the optimization time. Obviously, simply using a fixed transition point has been suggested as a poorer choice (Li et al. 2010) because: 1) the best positions of the transition points are constantly changing with the total number of iterations of heuristics, 2) the transition points usually were pre-determined by the researchers without considering the search pattern of heuristic algorithm, 3) the different strategies for generating candidate solutions may also have their own internal behavior which determines the searching path pattern (as showed in Pukkala and Heinonen 2008). Based on some profound insights of the search patterns of widely used heuristics, Bettinger et al. (1997) divided their search processes into three phases: a hill-climbing phase, an adjustment phase and a steady-state phase. Their work provides us insightful perspectives to continually optimize the hybrid techniques of heuristics in solving forest planning problems, and might also suggest the use of different oscillation patterns between 1-opt and n-opt moves within these phases of a s-metaheuristic search process.
Since heuristics only can provide acceptable solutions to difficult problems, rather than guarantee that the optimal solution will be located, thus the performance of heuristics should be evaluated carefully before applying them into forest management practices. Nowadays, five alternative methods have been widely used in the related literature (Zhu and Bettinger 2008): 1) evaluate the variation of various solution values; 2) compare against an exact LP solution (if possible); 3) compare against a relaxed LP solution; 4) compare against estimated global optimum solution; and 5) compare against other heuristics. Obviously, setting a baseline (i.e., the optimum objective function value) from mathematical programming (Method 2) is always the best way to evaluate the heuristic advantage and quality of the solution. However, it is certainly challenging to implement for a large, complex planning problem as presented in our study. Therefore, we only employed a relatively simple method (e.g., Method 1) to evaluate the performances of six alternative search strategies of simulated annealing. The slightly variation of 60 independent runs for each strategy pointed out the adequate solution stability of simulated annealing. Some modifications have recently been made to improve the handling ability of mathematical programming techniques in solving complex forest planning problems (e.g., Goycoolea et al 2009; Tóth et al 2013), which have provided some insights into evaluating the performance of heuristics.
Although the results in our research were only limited to one case and a small set of search parameters, it was compelling enough to illustrate the efficiency of different search strategies used for generating candidate solutions. However, application to a larger number of datasets will be important for analyzing the performance of different strategies for generating candidate solutions, because of the stochastic nature of simulated annealing algorithm. Some research has found that the size of a planning problem can also impose some explicit effects on the quality of solutions. For example, Bachmatiuk et al. (2015) found that changing the treatment schedule of more than one stand simultaneously did not improve the performance of simulated annealing if the combinatorial problems are very large, however if the size of the problem was reduced, then these types of 2-opt (or more) moves (changes, not exchanges) may perform better. Crowe and Nelson (2005) also found that the problem size does moderately affect the ability of simulated annealing to find near-optimal solutions, but the relationship between the size of problems and the quality of solutions was not great. In addition, since the target volumes and assigned cutting areas in this analysis were both relative small with respect to the large area (i.e., approximately 10% of the total number of management units), the planning problems might be not very difficult to solve. Obviously, increasing the levels of target volume might have significant effects on the performance of different search strategies, especially when the planning problems involve with the harvest adjacency and green-up constraints, however we have to leave this area of investigation for future research efforts.
As we suggested above, some natural extensions of this work would be more fully examine the effects of the tested search strategies on a larger number of datasets; other extensions would include extending this work to other s-metaheuristic processes, other forest planning problems (e.g., decreasing the fragmentation of over-mature forests in landscapes level), or other search enhancement techniques.
Acknowledgements
This work was supported by the Fundamental Research Funds for the Central University of China through the College of Forestry at the Northeast Forestry University (DL13EA05-03), the McIntire-Stennis project through the Warnell School of Forestry and Natural Resources at the University of Georgia (GEOZ-0168-MS) and the Fundamental Research Funds for the Central University of China through the College of Economic & Management at the Northeast Forestry University (2572015EC03). We also would like to express our deepest appreciation to the anonymous reviewers for their valuable comments and suggestions on our paper.
References
Arikan U., Gürel S., Aktürk M.S. (2016). Integrated aircraft and passenger recovery with cruise time controllability. Annals Operations Research 236(2): 295–317. http://dx.doi.org/10.1007/s10479-013-1424-2.
Bachmatiuk J., Garcia-Gonzalo J., Borges J.G. (2015). Analysis of the performance of different implementations of a heuristic method to optimize forest harvest scheduling. Silva Fennica 49(4) article 1326. http://dx.doi.org/10.14214/sf.1326.
Baskent E.Z., Jordan G.A. (2002). Forest landscape management modeling using simulated annealing. Forest Ecology and Management 165(1–3): 29–45. http://dx.doi.org/10.1016/S0378-1127(01)00654-5.
Bettinger P., Sessions J., Boston K. (1997). Using tabu search to schedule timber harvest subject to spatial wildlife goals for big game. Ecological Modelling 94: 111–123. http://dx.doi.org/10.1016/S0304-3800(96)00007-5.
Bettinger P., Sessions J., Johnson K.N. (1998). Ensuring the compatibility of aquatic habitat and commodity production goals in eastern Oregon with a Tabu search procedure. Forest Science 44(1): 96–112.
Bettinger P., Boston K., Sessions J. (1999). Intensifying a heuristic forest harvest scheduling search procedure with 2-opt decision choices. Canadian Journal of Forest Research 29: 1784–1792. http://dx.doi.org/10.1139/x99-160.
Bettinger P., Graetz D., Boston K., Sessions J., Chung W. (2002). Eight heuristic planning techniques applied to three increasingly difficult wildlife planning problems. Silva Fennica 36(2): 561–584. http://dx.doi.org/10.14214/sf.545.
Bettinger P., Boston K., Kim Y.H., Zhu J. (2007). Landscape-level optimization using tabu search and stand density-related forest management prescriptions. European Journal of Operational Research 176: 1265–1282. http://dx.doi.org/10.1016/j.ejor.2005.09.025.
Bettinger P., Sessions J., Boston K. (2009). A review of the status and use of validation procedures for heuristics used in forest planning. Mathematical and Computational Forestry & Natural-Resource Sciences 1(1): 26–37.
Bettinger P., Demirci M., Boston K. (2015). Search reversion within s-metaheuristics: impacts illustrated with a forest planning problem. Silva Fennica 49(2) article 1232. http://dx.doi.org/10.14214/sf.1232.
Borges P., Bergseng E., Eid T. (2014a). Adjacency constraints in forestry – a simulated annealing approach comparing different candidate solution generators. Mathematical and Computational Forestry & Natural-Resources Sciences 6(1): 11–25.
Borges P., Eid T., Bergseng E. (2014b). Applying simulated annealing using different methods for the neighborhood search in forest planning problems. European Journal of Operational Research 233: 700–710. http://dx.doi.org/10.1016/j.ejor.2013.08.039.
Boston K., Bettinger P. (1999). An analysis of Monte Carlo integer programming, simulated annealing, and tabu search heuristics for solving spatial harvest scheduling problems. Forest Science 45(2): 292–301.
Boston K., Bettinger P. (2001). Development of spatially feasible forest plans: a comparison of two modeling approaches. Silva Fennica 35(4): 425–435. http://dx.doi.org/10.14214/sf.578.
Boston K., Bettinger P. (2002). Combining tabu search and genetic algorithm heuristic techniques to solve spatial harvest scheduling problems. Forest Science 48(1): 35–46.
Caro F., Constantino M., Martins I., Weintraub A. (2003). A 2-opt tabu search procedure for the multiperiod forest harvesting problem with adjacency, greenup, old growth, and even flow constraints. Forest Science 49(5): 738–751.
Crowe K.A., Nelson J.D. (2005). An evaluation of the simulated annealing algorithm for solving the area-restricted harvest-scheduling model against optimal benchmarks. Canadian Journal of Forest Research 35(10): 2500–2509. http://dx.doi.org/10.1139/x05-139.
Dong L.B., Bettinger P., Liu Z.G., Qin H.Y. (2015). A comparison of a neighborhood search technique for forest spatial harvest scheduling problems: a case study of the simulated annealing algorithm. Forest and Ecology Management 356: 124–135. http://dx.doi.org/10.1016/j.foreco.2015.07.026.
Falcão A.O., Borges J.G. (2002). Combining random and systematic search heuristic procedures for solving spatially constrained forest management scheduling models. Forest Science 48(3): 608–621.
Fotakis D.G. (2015). Multi-objective spatial forest planning using self-organization. Ecological Informatics 29(1): 1–5. http://dx.doi.org/10.1016/j.ecoinf.2015.06.001.
Fuller J.D., Ramasra R., Cha A. (2012). Fast heuristics for transmission-line switching. IEEE Transactions on Power Systems 27(3): 1377–1386. http://dx.doi.org/10.1109/TPWRS.2012.2186155.
Golden B.L., Alt F.B. (1979). Interval estimation of a global optimum for large combinatorial problems. Naval Research Logistics Quarterly 26(1): 69–77. http://dx.doi.org/10.1002/nav.3800260108.
Goycoolea M., Murray A., Vielma J.P., Weintraub A. (2009). Evaluating approaches for solving the area restriction model in harvest scheduling. Forest Science 55: 149–165.
Heinonen T., Pukkala T. (2004). A comparison of one- and two-compartment neighborhood in heuristic search with spatial forest management goals. Silva Fennica 38(3): 319–332. http://dx.doi.org/10.14214/sf.419.
Hernandez M., Gómez T., Molina J., León M.A., Caballero R. (2014). Efficiency in forest management: a multiobjective harvest scheduling model. Journal of Forest Economics 20: 236–251. http://dx.doi.org/10.1016/j.jfe.2014.06.002.
Hof J., Flather C.H. (1996). Accounting for connectivity and spatial correlation in the optimal placement of wildlife habitat. Ecological Modelling 88: 143–155. http://dx.doi.org/10.1016/0304-3800(95)00082-8.
Kurttila M., Uuttera J., Mykrä S., Kurki S., Pukkala T. (2002). Decreasing the fragmentation of old forests in landscapes involving multiple ownership in Finland: economic, social and ecological consequences. Forest Ecology and Management 166: 69–84. http://dx.doi.org/10.1016/S0378-1127(01)00663-6.
Kurttila M., Pykäläinen J., Leskinen P. (2006). Defining the forest landowner’s utility-loss compensative subsidy level for a biodiversity objective. European Journal of Forest Research 125: 67–78. http://dx.doi.org/10.1007/s10342-005-0079-1.
Li R.X., Bettinger P., Boston K. (2010). Informed development of meta-heuristic for spatial forest planning problems. The Open Operational Research Journal 4: 1–11.
Liu G.L., Han S.J., Zhao X.H., Nelson J.D., Wang H.S., Wang W.Y. (2006). Optimization algorithms for spatially constrained forest planning. Ecological Modelling 194: 421–428. http://dx.doi.org/10.1016/j.ecolmodel.2005.10.028.
Los M., Lardinois C. (1982). Combinatorial programming, statistical optimization and the optimal transportation network problem. Transportation Research 16B: 89–124. http://dx.doi.org/10.1016/0191-2615(82)90030-3.
Lu F., Eriksson L.O. (2000). Formation of harvest units with genetic algorithms. Forest Ecology and Management 130: 57–67. http://dx.doi.org/10.1016/S0378-1127(99)00185-1.
Marshalek E.C., Ramage B.S., Potts M. (2014). Integrating harvest scheduling and reserve design to improve biodiversity conservation. Ecological Modelling 287: 27–35. http://dx.doi.org/10.1016/j.ecolmodel.2014.04.022.
McDill M.E., Braze J. (2001). Using the branch and bound algorithm to solve forest planning problems with adjacency constraints. Forest Science 47: 403–418.
McDill M.E., Rebain S.A., Braze J. (2002). Harvest scheduling with area-based adjacency constraints. Forest Science 48: 631–642.
Metropolis N., Rosenbluth A., Rosenbluth M., Teller A.H., Teller E. (1953). Equation of state calculations by fast computing machines. Journal of Biochemical and Biophysical Methods 21: 1087–1101. http://dx.doi.org/10.1063/1.1699114.
Murray A.T. (1999). Spatial restrictions in harvest scheduling. Forest Science 45: 45–52.
Öhman K., Lämås T. (2003). Clustering of harvest activities in multi-objective long-term forest planning. Forest Ecology and Management 176: 161–171. http://dx.doi.org/10.1016/S0378-1127(02)00293-1.
Pukkala T. (2014). Does biofuel harvest and continuous cover management increase carbon sequestration? Forest Policy and Economics 43: 41–50. http://dx.doi.org/10.1016/j.forpol.2014.03.004.
Pukkala T., Kurttila M. (2002). Examining the performance of six heuristic optimization techniques in different forest planning problems. Silva Fennica 39(1): 67–80. http://dx.doi.org/10.14214/sf.396.
Pukkala T., Heinonen T. (2006). Optimizing heuristic search in forest planning. Nonlinear Analysis-Real World Applications 7: 1284–1297. http://dx.doi.org/10.1016/j.nonrwa.2005.11.011.
Richards E.W., Gunn E.A. (2000). A model and tabu search method to optimize polygon harvest and road construction schedules. Forest Science 46: 188–203.
Shan Y., Bettinger P., Cieszewski C., Wang W. (2012). Pitfalls and potential of particle swarm optimization for contemporary spatial forest planning. Forest Systems 21(3): 468–480. http://dx.doi.org/10.5424/fs/2012213-03692.
Sinclair K., Cordeau J.F., Laporte G. (2014). Improvements to a large neighbourhood search heuristic for an integrated aircraft and passenger recovery problem. European Journal of Operational Research 233: 234–245. http://dx.doi.org/10.1016/j.ejor.2013.08.034.
State Development Planning Commission and State Forestry Bureau. (2010). The ecological protection and economic transformation plans of Great Xing’an Mountain in 2010–2020. Chinese Forestry Press, Beijing.
Strimbu B.M., Innes J.L., Strimbu V.F. (2010). A deterministic harvest scheduler using perfect bin-packing theorem. European Journal of Forest Research 129: 961–974. http://dx.doi.org/10.1007/s10342-010-0405-0.
Tang M.P., Tang S.Z., Lei X.D., Li X.F. (2004). Study on spatial structure optimizing model of stand selection cutting. Scientia Silvae Sinicae 40(5): 25–31. [In Chinese with an English abstract].
Tóth S.F., McDill M.E., Könnyü N., George S. (2013). Testing the use of lazy constraints in solving area-based adjacency formulations of harvest scheduling models. Forest Science 59: 157–176. http://dx.doi.org/10.5849/forsci.11-040.
Zhu J.P., Bettinger P. (2008). Estimating the effects of adjacency and green-up constraints on landowners of different sizes and spatial arrangements located in the southeastern U.S. Forest Policy and Economics 10(5): 295–302. http://dx.doi.org/10.1016/j.forpol.2007.11.006.
Total of 49 references.

