Effect of pruning season and tool on knot occlusion and stem discolouration in Betula pendula – situation five years after pruning
Niemistö P., Kilpeläinen H., Heräjärvi H. (2019). Effect of pruning season and tool on knot occlusion and stem discolouration in Betula pendula – situation five years after pruning. Silva Fennica vol. 53 no. 1 article id 10052. https://doi.org/10.14214/sf.10052
Highlights
- The occlusion was the fastest in the case of small living branches of fast growing trees pruned in springtime
- Occlusion was quicker after saw pruning than after secateurs pruning, due to shorter knot stubs
- Branches that were pruned in living state occluded faster than the ones pruned as dead
- Dead branches hit down with a stick occluded slowly.
Abstract
This paper investigates and models the effects of pruning season and tool on wound occlusion with varying tree and branch characteristics of silver birch (Betula pendula Roth) stems at the pruning height of 0−4 metres. Dates of eight secateurs prunings, three saw prunings and two sticks prunings as well as unpruned control were tested in permanent plots on four sites. Knot occlusion and discolouration in stemwood were measured from about 1600 studied knots of 112 sample trees felled five to six years after pruning in 2010. Knot occlusion rate was modelled according to pruning tool, date, tree growth, and branch characteristics. The occlusion was the fastest in trees pruned in spring or early summer, and the slowest in trees pruned in autumn. Stubs of living branches occluded faster than the dead ones with the same diameter. Saw pruning resulted in clearly better occlusion rates than secateurs pruning, caused by the shorter knot stubs after saw pruning. Hitting dead branches away with a stick resulted in the worst occlusion status. The colour defects spread more often upward from the knot than downward. Discolouration in stemwood was detected more frequently near to the pruned branches than the unpruned ones, and more widely near to the stubs of dead branches than the living ones. Most saw and secateurs pruned branches were completely occluded during the experiment, so these prunings were suitable for all branches under 20 mm in diameter, and for living branches even up to 30 mm in fast-growing trees.
Keywords
silver birch;
pruning saw;
discolouration;
healing-over;
secateurs;
stick pruning
-
Niemistö,
Natural Resources Institute Finland (Luke), Natural resources, Kampusranta 9 C, FI-60320 Seinäjoki, Finland
E-mail
pentti.niemisto@luke.fi

- Kilpeläinen, Natural Resources Institute Finland (Luke), Production systems, Yliopistokatu 6 B, FI-80100 Joensuu, Finland E-mail harri.kilpelainen@luke.fi
- Heräjärvi, Natural Resources Institute Finland (Luke), Production systems, Yliopistokatu 6 B, FI-80100 Joensuu, Finland E-mail henrik.herajarvi@luke.fi
Received 2 October 2018 Accepted 4 March 2019 Published 11 March 2019
Views 133990
Available at https://doi.org/10.14214/sf.10052 | Download PDF

1 Introduction
Pruning of forest trees aims at improving the tree architecture (formative pruning), increasing the stem value by increased production of knot-free wood (high pruning or silvicultural pruning) (Nicolescu 1999), reducing the fire hazard risk, or improving the visual or aesthetic appeal of the forest (Hanley et al. 1995). Formative pruning is most often carried out for deciduous species with a sympodial growing pattern, whereas silvicultural pruning can be applied for all grown species.
Two birch species (Betula pendula Roth and Betula pubescens Ehrh.) have industrial uses in Northern Europe. Of these, B. pendula is the predominant plantation species due to its better average stem quality and faster growth (Verkasalo 1997; Heräjärvi 2002; Hytönen et al. 2014). The methods and profitability of silvicultural pruning of B. pendula were first analysed for the needs of the plywood industry in Finland based on studies initiated in the 1930s (Lappi-Seppälä 1934; Laitakari 1937; Lehonkoski 1949). The first veneer peeling experiments on pruned birch logs revealed severe internal damage, based on which finding birch pruning was judged unprofitable. Heiskanen (1958), however, questioned the unprofitability of birch pruning and estimated that the damage observed in the early peeling experiments was caused partly by mistakes in the pruning work, such as pruning oversized branches and wrong or careless work methods, and partly by the selection of the wrong trees for pruning. The following, more detailed studies confirmed that pruning can increase the value of birch butt logs for plywood, veneer, or sawn wood production (Heiskanen 1958). Later, the effects of pruning on birch wood quality were studied by Vuokila (1976), Raulo et al. (1978), Verkasalo and Rintala (1998), Kannisto and Heräjärvi (2006), Schatz et al. (2008), Wang et al. (2016), and Stener et al. (2017). The economic aspect of birch pruning has been studied by Holopainen (1949), Heiskanen (1966a), and Kannisto and Heräjärvi (2006) who calculated that if pruned B. pendula is harvested when the diameter at breast height reaches 29–30 cm, the forest owner can get a 4–5 per cent return on the pruning investment.
Birch trees have been pruned by three main methods: pruning saw, secateurs, and so-called stick pruning. Stick pruning, in which the branch is removed from the stem by a hit with a stiff wooden or metal pole, can be applied for dead branches only, whereas the other methods are technically applicable for both living and dead branches. The currently applied Finnish birch pruning recommendations advise pruning only the best quality trees with less than 20 mm thick living or dead branches (Äijälä et al. 2014). Thicker than 20 mm branches occlude slower and have higher risk to spread colour on surrounding stemwood (Verkasalo and Rintala 1998; Schatz et al. 2008). Thin branches would likely self-prune as a result of canopy suppression and subsequent branch dying, but then the volume of knot-free wood would be smaller and unpredictable. Thus, pruning enables estimating or modelling the volume of knot-free wood in a butt log. When planted silver birch is grown following the stand densities of the current silvicultural recommendations in Finland, the branch diameters rarely exceed 30 mm in the remaining trees after the first commercial thinning (Niemistö 1995a; Mäkinen et al. 2003) and only birches with thin branches are pruned. Branches should be cut as close as possible to the stem but still without damaging the branch collar that initiates the occlusion process of the pruning wound. At least 50% of the tree’s height should be left for the living crown in order to not decrease growth. Summer from mid-June to early August, as well as early spring, are the recommended seasons for birch pruning due to the lowest risk of discolouration (Verkasalo and Rintala 1998).
Based on the studies of the 2000s (Kannisto and Heräjärvi 2006; Schatz et al. 2008), secateurs have become the recommended tool for birch pruning, since they appear to decrease the risk of discolouration in comparison to pruning saws. Kannisto and Heräjärvi (2006) listed reasons to use secateurs instead of pruning saws: smoother cross cut surface in the branch, thus, less contact area for fungal spores to enter; more exact determination of the cross-cutting point of a branch; lower risk of tear damage in the branch collar or stem bark; and lower risk of stem damage in small trees that easily vibrate during pruning saw strokes. According to Skovsgaard et al. (2018), the time consumption of pruning work increased with the number and thickness of branches and with the pruning height but was also highly dependent on the operator and the model of pole saw used. Heiskanen (1963) emphasized also the influence of the stem size (which is correlated with the branch size) and the length of the pruned stem section (pruning height) on the time consumption. For thick branches, so-called target pruning (cutting perpendicular to the branch) is faster than flush pruning (cutting parallel to the stem) (O’Hara 2007; Skovsgaard et al. 2018).
The two most important quality attributes related to pruning are the speed of occlusion of branch stubs and the discolouration of the stem via pruning wounds. In the case of B. pendula, studies related to these variables (Heiskanen 1958; Vuokila 1976; Verkasalo and Rintala 1998; Vadla 1999; Kannisto and Heräjärvi 2006; Schatz et al. 2008) show slightly contradictory results in regard to the pruning methods, seasons, and the vitality status (living/dead) of the pruned branches. In addition, most of the results are based on experiments in which pruning has been carried out by a saw. Due to the contradictory findings and lack of systematic results for secateurs pruning, the Finnish Forest Research Institute established a comprehensive B. pendula pruning experiment in 2004. The experimental setup takes into account several pruning methods and dates from March to September. Pruning is a potential way to improve the stem quality and income expectations from birch stands. Because of the uncertainties related to pruning methods and their effects on wood quality, it is justified to compare the methods using systematic data.
The objective of this study is to report the occlusion and discolouration results for the trees that were felled and examined five to six growing seasons after pruning. Based on the measurements of the studied trees, the occlusion rate of knots and the discolouration in stemwood were compared with 14 different treatments, which included 3 saw, 8 secateurs, and 2 stick prunings during various seasons, as well as unpruned control. Also, we examine how the growth of the tree, as well as the size and vitality of a pruned branch affected the occlusion process of a knot.
2 Materials and methods
2.1 Pruning experiment
The experiment was established in four even-aged planted silver birch (B. pendula) stands on fertile mineral soils in 2004. Stand A was located in herb-rich forest land and other three stands (B−D) on former agricultural fields (Table 1). This division between sites depicts quite well the Finnish birch plantations established in the 1990s. Study stands were selected using the criteria that self-pruning had not occurred yet and the butt log section (0–4 m from the stump) had both dead and living branches up to approximately 30 mm in diameter. One to three rectangular sample plots were established per stand, thus comprising the total number of eight sample plots in this study.
| Table 1. Locations, areas, and main characteristics of the growing stock in eight sample plots at the beginning of the pruning experiment in spring 2004 and after six growing seasons in winter 2009–2010. | ||||||||||
| Stand, location and coordinates (WGS84) | Plot | Plot area, m3 | Number of stems, ha–1 | Crown base, m | Dominant height, m | Mean dbh, mm | Volume, m3 ha–1 | |||
| 2004 | 2004 | 2004 | 2010 | 2004 | 2010 | 2004 | 2010 | |||
| A Padasjoki (61°26´N, 25°06´E) | 1 | 680 | 1838 | 3.2 | 11.5 | 16.6 | 94 | 124 | 65 | 143 |
| 2 | 990 | 1444 | 2.0 | 12.2 | 15.5 | 96 | 130 | 47 | 116 | |
| B Kuhmoinen (61°36´N, 25°18´E) | 3 | 770 | 1481 | 1.3 | 10.4 | 15.7 | 79 | 117 | 31 | 102 |
| 4 | 1076 | 1571 | 1.7 | 9.6 | 15.2 | 73 | 109 | 25 | 83 | |
| 5 | 828 | 1546 | 2.0 | 11.4 | 17.5 | 88 | 121 | 44 | 120 | |
| C Parkano (62°02´N, 23°02´E) | 6 | 600 | 1650 | 3.2 | 12.1 | 17.1 | 102 | 138 | 66 | 158 |
| 7 | 600 | 1650 | 3.3 | 11.9 | 16.9 | 102 | 139 | 66 | 161 | |
| D Parkano (61°59´N, 22°56´E) | 8 | 600 | 2033 | 3.1 | 11.4 | 16.2 | 93 | 126 | 63 | 167 |
| Mean | 768 | 1652 | 2.5 | 11.3 | 16.4 | 91 | 126 | 51 | 131 | |
All trees on the sample plot were numbered as tally trees. Their locations with respect to the cardinal directions and distance from the center point of the sample plot and diameters at the breast height (dbh) were measured in spring 2004. Dominant trees with acceptable quality and growth expectations were selected from each plot to comprise the base population, and three trees per each treatment were randomly selected as sample trees. The area of the sample plot (600−1076 m2) was dependent on the possibility of finding 42 sample trees from each particular plot. Tree height and crown limits as well as stem diameters at stump height and at 4-m height were measured for sample trees before pruning. All diameters were measured over bark in two cardinal directions. The dbh of all sample trees were remeasured after one growing season in autumn 2004.
The mean dbh of all trees in the sample plots varied between 7.3 and 10.2 cm (9.1 cm on average), and the mean dominant height varied between 9.6 and 12.2 m (11.3 m on average) depending on the plot (Table 1). Thus, according to the birch management guidelines in Finland (Äijälä et al. 2014), the stands had not achieved the dimensions of the first commercial thinning 13–14 years after planting. The trees in the stand B were slightly smaller than the ones in the other stands. Branches in sample trees had died up to 2.5 m, on average. However, the natural pruning had proceeded no higher than 0.5 m above ground.
The 14 different treatment combinations selected in this study included 8 secateurs pruning dates from early spring to autumn, 3 saw pruning dates (early spring, summer, early autumn), and stick pruning of dead branches in autumn 2004 and spring 2005, as well as unpruned controls (Table 2). Each treatment was repeated for three trees in every sample plot.
| Table 2. Numbers (N), mean diameters at breast height (dbh) over bark in spring 2004 and winter 2009–2010, and annual dbh increments of felled study trees during the experiment for different pruning treatments (standard deviations presented in parentheses and ranges between minimum and maximum values). | ||||||||
| dbh 2004, mm | dbh 2010, mm | dbh increment, mm a–1 | ||||||
| Pruning method | Pruning date | N | Mean (Sd) | Range (min-max) | Mean (Sd) | Range (min-max) | Mean (Sd) | Range (min-max) |
| Secateurs | 19.3.2004 | 8 | 97 (13) | 79–117 | 134 (11) | 119–149 | 6.2 (1.2) | 4.4–8.0 |
| Saw | 19.3.2004 | 8 | 95 (16) | 73–123 | 131 (18) | 100–155 | 5.9 (1.0) | 4.5–7.5 |
| Secateurs | 29.4.2004 | 8 | 88 (16) | 64–113 | 124 (15) | 102–143 | 5.9 (0.8) | 4.8–7.2 |
| Secateurs | 3.6.2004 | 8 | 93 (10) | 75–103 | 133 (11) | 118–152 | 6.7 (1.7) | 4.3–9.2 |
| Secateurs | 23.6.2004 | 8 | 96 (9) | 80–103 | 131 (13) | 113–145 | 5.9 (1.1) | 4.9–7.6 |
| Secateurs | 15.7.2004 | 8 | 91 (14) | 76–117 | 124 (15) | 105–149 | 5.4 (1.3) | 3.4–7.8 |
| Saw | 15.7.2004 | 8 | 92 (12) | 75–106 | 130 (20) | 101–159 | 6.3 (2.1) | 2.9–9.8 |
| Secateurs | 5.8.2004 | 8 | 95 (14) | 68–119 | 135 (21) | 104–176 | 6.6 (1.4) | 5.1–9.5 |
| Secateurs | 26.8.2004 | 8 | 96 (22) | 64–136 | 139 (31) | 96–191 | 7.1 (1.9) | 4.5–9.3 |
| Saw | 26.8.2004 | 8 | 98 (20) | 69–118 | 134 (22) | 97–161 | 5.9 (0.9) | 4.7–7.2 |
| Secateurs | 16.9.2004 | 8 | 95 (16) | 79–119 | 136 (21) | 115–166 | 6.8 (1.2) | 5.3–9.0 |
| Stick | autumn 2004 | 8 | 87 (13) | 70–104 | 122 (17) | 101–149 | 5.8 (1.5) | 2.8–7.4 |
| Stick | spring 2005 | 8 | 90 (15) | 70–115 | 127 (14) | 106–146 | 6.1 (1.2) | 3.8–7.3 |
| Control | not pruned | 8 | 96 (15) | 76–123 | 131 (14) | 114–153 | 5.9 (0.6) | 5.0–6.8 |
| ALL DATA | 112 | 94 (14) | 64–136 | 131 (18) | 96–191 | 6.2 (1.3) | 2.8–9.8 | |
All sample trees were pruned according to the pre-determined treatment except the unpruned control trees. Notes were made on any damage caused to the stem or bark during pruning. The workers were advised to do the work as target pruning (cutting direction normal to the branch longitudinal axis). However, especially in the case of saw pruning of upright branches, the result was closer to flush pruning, i.e., parallel to the stem surface. The area of the pruning wound is minimized in target pruning, but on the other hand, the remaining branch stub is typically slightly longer than in flush pruning.
The vitality status (living/dead) of all branches with a diameter greater than 10 mm was assessed, and the branch diameters were measured over bark in both horizontal and vertical directions perpendicular to the longitudinal axis of the branch. Distance from the ground and compass direction were also recorded for each pruned branch over 10 mm in diameter. Thus, it was possible to identify the knots on the trunks at the time of stem analysis. Moreover, the number of small (diameter < 10 mm) branches were counted from the butt to the 4-m height.
Secateurs pruning was accomplished with Fiskars single hand bypass secateurs up to approximately two metres and with Fiskars pole secateurs from 2 to 4-m heights (see www.fiskars fi). A small-toothed handsaw and Fiskars and Bahco pole saws (see www.bahco.com) were used as the tools for saw pruning. Stick pruning was carried out with a stiff wooden pole by hitting dead branches near to the stem surface from above. Living branches in stick pruned trees were left untouched.
2.2 Follow-up measurements and study tree felling
All trees in the sample plots were re-measured in winter 2009–2010 in the same manner as at the establishment of the experiment (Table 1). The dominant height and mean dbh were now 16.4 m and 12.6 cm, respectively. The mean annual volume increment in the 6-year period varied between 10 and 17 m3 ha–1 (13.4 m3 ha–1 on average). The mean increments of the basal area-weighted dbh and dominant height were 5.8 mm a–1 and 84 cm a–1, respectively.
One third of the sample trees (one tree per treatment in each plot) were randomly selected for this study, i.e., for felling and further analysis, on March 2010. The mean dbh of these selected trees (N = 112) had increased from 94 to 131 mm during six growing seasons, which means an approximate annual dbh increment of 6.2 mm (Table 2). The mean dbh of the felled study trees varied between 87 and 98 mm in 2004, and the average dbh increment varied between 5.4 and 7.1 mm a–1 depending on the treatment.
The direction relative to the north, as well as the 1.3-m height was marked on the stems before felling. The diameters of the felled study trees were recorded over bark from the base cut and at the heights of 50, 100, 130, and 150 cm and from that on at every 50 cm up to the height of 6 m. Two 2.5-m-long logs were cut from the base of the stems and encoded for identification. Remaining branches found in the logs of the control and stick pruned trees were carefully delimbed with a chainsaw and measured in the same way as the branches cut in the pruning phase. The knots above the pruning section at the height of 4−5 m of all study trees were delimbed and measured identically but not used in this study. Halves, totalling 448 originating from 112 trees, were encoded with the necessary identification information, piled loosely with stickers, covered, and stored outdoors.
2.3 Measurements of study stems and knots
After the storage period, all halves were transported to the laboratory where all pruned and unpruned branches and knots thicker than 10 mm in diameter were located on the log halve surface and identified according to the heights and directions of the branches measured before pruning. In this study, a knot refers to the part of the branch that is located inside the trunk. However, also the branch stub remaining after the pruning is considered as a part of the knot. Visible knot scars and stubs, which were not noted and measured in the forest, being mostly less than 10 mm in diameter, were also located over bark. Furthermore, the wound occlusion phase of all knots was externally evaluated from the surface according to the following classes:
1 - Unpruned branch or occlusion not started
2 - Visible knot stub
3 - Occlusion underway but wound still open
4 - Wound closed but visible
5 - Scar visible but wound not visible
The log halves were cross-cut into approximately 15-cm-long pieces with a knot in the centre. Such knot pieces from the heights of 0–4 m of 112 felled study trees comprised the knot analysis material of this study (Table 3, Supplementary file S1). Most of them (1379 knots) were measured already in the forest, whereas the other 258 knots represented smaller than 10 mm thick or self-pruned knots that were not identified until they were in the laboratory. Living branches were not stick-pruned, thus, a total of 48 such knots in stick-pruned trees were excluded from the study data.
| Table 3. Main characteristics of study branches. Numbers (N) and mean vertical diameters (measured in 2004 over bark) are presented for living, dead, and all branches in total and separately for different pruning treatments (standard deviations in parentheses and ranges between minimum and maximum values). Cumulative radial increments (over bark) of felled study trees at the height of each branch during five to six growing seasons were also determined for all branches. View in new window/tab. |
The knot pieces were further processed so that the knot was split into two halves, and the one with better split knot appearance was used in image scanning. If two or more knots were close to each other, i.e., located in the same knot piece, the largest one was selected for the analysis, and the others were rejected. As a result of this selection and the fact that some knots were lost due to the unsuccessful preparation process, the total number of knots accepted for the study material was 1637.
These split study knots were numbered and scanned into images (Fig. 1). The occlusion of each knot was visually determined from the images using classes 1–8:
1 - Occluded without discolouration
2 - Occluded with some discolouration
3 - Partly occluded from both the up- and downside of the knot
4 - Partly occluded from either the up- or downside of the knot
5 - Occlusion just started, a visible protrusion outside the knot
6 - Occlusion not started
7 - Unpruned dead branch
8 - Unpruned living branch

Fig. 1. Three scanned images of study knots: Knot 1A: a 12-mm-thick knot occluded without discolouration (occlusion class 1). The occlusion gap was closed and the occlusion rate was set to 100%. Knot 1B: occlusion started from the up and down sides of a 16-mm-thick knot (class 3). Because the occlusion gap (G) was 7.7 mm long, the occlusion percentage was 52%. Knot 1C: vertical diameter of the knot was 13 mm and the occlusion gap was not measured because no occlusion was observed (class 6). The occlusion rate was set to 0%. A small discolouration in the stemwood (upward only↑) was also detected.
Only occluded knots were divided into classes 1 and 2 according to discolouration in stemwood, because we wanted to know the percentages of knots occluded without discolouration. In other occlusion classes discolouration was not taken into account.
The non-occluded gap (line segment G in Fig. 1, knot 1B) was measured from all saw and secateurs pruned knots in which the occlusion was started but not completed (i.e., knots belonging to occlusion classes 3–5). The proportion of the non-occluded gap from the vertical diameter of a knot was defined as the occlusion percentage for the pruned knot. This percentage was set to 0for knots with no occlusion observed in classes 6–8 (Fig. 1, knot 1C) and to 100 for occluded knots in classes 1–2 (Fig. 1, knot 1A). Occlusion percentages were defined from 1344 saw and secateurs pruned knots.
The discolouration in the stemwood was measured upward and downward from each knot using image analyses of the cross-cut surface of the longitudinally split knots (Fig. 1, knot 1C). Only the maximum distance of discolouration spreading in both directions was recorded. The maximum measured colour spreading distance was set to 75 mm because of the size of the split knot specimens. Colour defects, which were in connection with large stem discolouration of undefined origin, were observed in 52 knots. These specimens were excluded from the knot discolouration analyses; thus, the total number of knots in these analyses was 1585.
2.4 Data analysis
Besides the statistical models, we report the actual numbers of study knots in each occlusion class according to the pruning treatments and the average occlusion percentages for stubs of living and dead branches in saw and secateurs prunings five to six years after the pruning. We also present the preliminary results of the discolouration measurements in the stemwood. The average percentages of discoloured knots and the mean colour spreading distances from the knot are presented for living and dead branches.
The growth of the tree affects the occlusion speed after pruning or other wounding of the stem (Roth 1948; O’Hara et al. 1996; Stener et al. 2017). In order to model the knot occlusion, we determined the cumulative radial increment of each study tree from the time of pruning (or from the beginning of the experiment in the case of unpruned trees) to the felling date at the height of each study knot. In the calculation of radial increments at different heights of a sample tree, first two separate taper curves for each tree were linearly interpolated according to the stem diameters measured at the heights of 1.3 and 4.0 m. These curves were made for pruned trees before and after the growing season in 2004 and at the time of felling in winter 2009–2010. Finally, the cumulative radial increment over bark at the height of each knot in a sample tree was calculated using the stem diameters interpolated from these taper curves to the corresponding height of the tree (Table 3). Since the trees were pruned throughout the growing season in 2004, the radial increment from the pruning date to the end of the growing season in 2004 was taken into account using the girth band measurements of silver birch by Niemistö (2013). In unpruned control trees, the cumulative radial increments were calculated from the beginning of the study to the time of tree felling.
The total numbers and mean vertical diameters of the study branches according to the treatment and vitality of the branch are presented in Table 3. The study data consisted of 1637 branches including 358 branches with saw prunings, 1000 branches with secateurs prunings, 163 branches with stick prunings, and 116 branches with no pruning (control) (see Suppl. file S1). On average, 117 branches were measured for each treatment and 15 branches from each felled study tree.
Approximately two thirds of the branches were dead and one third living before pruning in 2004. In this study data, the living branches had diameters that were on average 3 mm larger than in the dead ones, but the mean diameter of branches varied a lot between treatments. The mean vertical diameter of the branches was the highest (17.4 mm) in study trees pruned with a saw on July 15th. The lowest diameter (9.3 mm) was in unpruned trees, because of the large number of small branches that were not located until the samples were in the laboratory. The mean cumulative radial increment of the felled study trees at branch height was approximately 18 mm from the pruning time to the felling of trees in 2010.
Because horizontal diameters of some small-sized branches (with the vertical diameter under 10 mm) or other not pre-localized knots were not measured in the field, the missing horizontal diameters (y) for these branches were estimated using a simple regression model (Eq. 1) in which the vertical diameter of a branch (x) was used as the only predictor.
![]()
This modelling data from felled study trees consisted of 1707 branches with known vertical and horizontal diameters at the height of 0–4 m above ground level. Because not all these branches were measured and processed in the laboratory, this data contained a lot of branches excluded from the modelling data for knot occlusion (Models 1–4 in Table 4). Means and standard deviations for the measured branches were 13.4 and 3.9 mm vertically and 15.1 and 5.0 mm horizontally, respectively. The coefficient of determination (R2) of this model was 0.87.
| Table 4. Observation methods used in this study to identify external and internal occlusion classes as well as occlusion percentages for knots in alternative pruning treatments and four differently formulated models to analyse the knot occlusion. | ||||
| Dependent variable of occlusion | External occlusion class | Internal occlusion class | Occlusion percentage of a knot | |
| Origin | From stem surface | From split knots | From split knots | |
| Observation method | External evaluation, 6 classes | Internal evaluation, 8 classes | Exact measurement (0.1 mm), occlusion % of a knot | |
| Model formulation | Not modelled | Ordinal regression models with mixed-effects (Eq. 2–4) | Linear mixed models (Eq. 5) | |
| Modelling: | ||||
| 1) Effect of pruning date | Data: Treatments: | MODEL 1 1000 knots Secateurs 8 dates | ||
| 2) Effect of pruning method and season | Data: Treatments: | MODEL 2 1001 knots 1) Secateurs 3 dates Saw 3 dates Stick 2 dates Control | MODELS 3 and 4 1334 knots Secateurs 8 dates Saw 3 dates | |
| 1) includes only equal dates for saw and secateurs pruning. | ||||
The basic unit in the subsequent statistical analyses was “a knot”, but the analysis knot data consisted also of the hierarchical structure of stands, sample plots, sample trees, and study knots. Because measurements of the knots in the same tree were also correlated, we formulated multi-level mixed-effect models and tested whether the pruning method and date affected the occlusion rate of study knots five to six years after pruning by using two different statistical analyses (Table 4). In the first analysis, which used ordinal regression modelling with mixed effects, the knot’s occlusion class was set as the response variable. In the second analysis, i.e., linear mixed modelling, the response variable was the arcsine transformation of a knot’s occlusion rate (expressed as a proportion ranging in value between 0and 1, which corresponds also to the occlusion percentages between 0and 100%). Because only few sample trees (one sample tree per treatment) were measured in each sample plot, sample plot was dropped out of the mixed-effect models so stand and sample tree were selected to random effects in all the models.
First, ordinal regression models with mixed effects were formulated for estimating the knot’s occlusion class (Y), which was used as a categorical response variable in the models. The ordinal regression model is an extension of the logistic model for binary data. We used a proportional odds model which is based on cumulative properties (Walker and Duncan 1967; McCullagh 1980). Because observations were divided smoothly between the classes of the response variable Y, the link function logit was chosen.
The ordinal regression model (or cumulative link model) with the random effect u (only intercept) is composed of j models in which the constant term α varies and coefficients β stay the same, as follows:
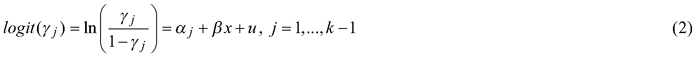
where γj is a cumulative probability for the occlusion class j, x is as a set of independent variables and k is the number of different occlusion classes. The random part u of the model can be formulated as us + uis in which us refers to the random effect of the stand s and uis to the random effect of the tree i in the stand s.
Cumulative probabilities γj for each occlusion class j were calculated in the model as:
![]()
Probability estimates p can be obtained as:

Because the occlusion class was used as a category variable (Y), the classification of each knot into a specified occlusion class was predicted using two different mixed-effect models of the ordinal response data (Eq. 2–4) for secateurs pruned branches and for variously pruned or unpruned branches. In the first model (Model 1) the effect of the pruning date on the probability of the occlusion class for a pruned knot was modelled using the internal grading of study knots pruned by secateurs at eight different dates (Table 4). According to this analysis, all secateurs pruned knots (1000 knots in total, see Suppl. file S2) fell into occlusion classes 1–6 (Table 5). The pruning date (category), the vitality of the branch (category), the horizontal diameter of the branch over bark before pruning (mm, continuous), and the cumulative radial increment (from the date of pruning to the felling date of study trees) of the tree at the branch height (mm, continuous) were set as fixed effects in this model.
| Table 5. Distribution of silver birch knots into occlusion classes according to the pruning method (sc = secateurs, sw = saw, stick = stick pruning) and date. Classification is made internally from the cross-cut surface of longitudinally split knots five to six growing seasons after pruning. | ||||||||||||||||
| Number of knots according to different pruning treatments (i.e., various methods and dates) | ||||||||||||||||
| Sc | Sw | Sc | Sc | Sc | Sc | Sw | Sc | Sc | Sw | Sc | Stick | Stick | Control | Total | ||
| Occlusion class | 19.3. | 19.3. | 29.4. | 3.6. | 23.6. | 15.7. | 15.7. | 5.8. | 26.8. | 26.8. | 16.9. | autumn | spring | N | % | |
| 1 – Occluded without discolouration | 46 | 34 | 27 | 28 | 16 | 6 | 18 | 13 | 10 | 19 | 18 | 10 | 5 | 3 | 253 | 15 |
| 2 - Occluded with some discolouration | 67 | 59 | 53 | 65 | 30 | 26 | 57 | 27 | 21 | 23 | 28 | 27 | 27 | 3 | 513 | 31 |
| 3 - Partly occluded from both the up- and downside of the knot | 21 | 22 | 27 | 23 | 26 | 30 | 27 | 24 | 22 | 26 | 19 | 10 | 4 | 1 | 282 | 17 |
| 4 - Partly occluded from either the up- or downside of the knot | 10 | 1 | 17 | 14 | 37 | 28 | 10 | 47 | 21 | 20 | 35 | 8 | 11 | 2 | 261 | 16 |
| 5 - Occlusion just started, a visible pro-trusion outside the knot | 2 | 3 | 4 | 0 | 12 | 20 | 6 | 9 | 13 | 17 | 19 | 4 | 6 | 0 | 115 | 7 |
| 6 - Occlusion not started | 0 | 0 | 1 | 1 | 7 | 9 | 7 | 5 | 12 | 9 | 4 | 19 | 32 | 3 | 109 | 7 |
| 7 - Unpruned dead branch | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 92 | 92 | 6 |
| 8 - Unpruned living branch | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | 12 | 1 |
| All knots | 146 | 119 | 129 | 131 | 128 | 119 | 125 | 125 | 99 | 114 | 123 | 78 | 85 | 116 | 1637 | 100 |
| All knots of living branches | 43 | 39 | 69 | 78 | 55 | 54 | 68 | 67 | 50 | 37 | 44 | - | - | 36 | 640 | 39 |
| All knots of dead branches | 103 | 80 | 60 | 53 | 73 | 65 | 57 | 58 | 49 | 77 | 79 | 78 | 85 | 80 | 997 | 61 |
The second ordinal regression model (Model 2) was constructed for 1001 saw, secateurs, and stick pruned knots and unpruned branches (Table 4 and Suppl. file S2). The internally evaluated class of knot occlusion (Y) was used as a category response variable with eight ordered classes (see valid classes 1–8 in Table 5). The selected treatments were three saw and three secateurs pruning times (19 March, 15 July, and 26 August 2004), two stick pruning times (autumn 2004 and spring 2005), and the control (no pruning). The pruning date as an independent variable was not included in this occlusion model because of the differences in the timings of saw, secateurs, and stick pruning. Thus, all combinations of pruning tools and dates were treated as independent treatments in this model. Predictor variables were the same as in Model 1 except for the vitality of a branch, which was not statistically significant and was dropped from Model 2. Moreover, in the case of stick pruning, only dead branches were knocked down and included in this analysis.
In the second analyses based on linear mixed models we used an arcsine transformation of the wound occlusion proportion p’ for each knot as follows:
![]()
where α and β are from the data estimated parameters, x is as a set of independent variables, and u is a random effect (only intercept) consisting of the sum of the random effects of the stand s and of the tree i in the stand s (u = us + uis).
A binomial distribution is common for variables with percentage values (or proportions), because many observations were close to the values 0% and 100% (or 0and 1). Thus, we used an arcsine transformation to normalize the distribution of the dependent variable (Zar 1984):
![]()
where p is the percentage of the non-occluded gap from the vertical diameter of a knot (range 0–100%).
The wound occlusion rate, denoted as the proportion of the knot diameter (exactly, the arcsine transformation of that) was estimated using two different linear mixed models (Eq. 5) for saw and secateurs pruned branches. This modelling data consisted of 1334 knots located 0–4 m above the ground in saw and secateurs pruned study trees (Table 4 and Suppl. file S2). The non-occluded gap was not measured from ten knots which were not included in this analysis data. Saw and secateurs prunings were combined in the modelling into three seasonal classes as follows: spring prunings were made on 19 March, 29 April, or 3 June, summer prunings on 23 June, 15 July, or 5 August, and autumn prunings on 26 August or 16 September.
In the modelling occlusion rates for saw and secateur pruned branches, the vitality of a branch (living or dead), the pruning method (saw or secateurs), and the three pruning seasons: spring, summer and autumn were used as category variables as well as the continuous variables “height of a branch above ground” and “vertical diameter of a branch”. In the causal-like Model 3 (Table 4), the growth variable used was “cumulative net radial growth on branch height”, the same variable as used previously in predicting the occlusion classes in Models 1 and 2.
In the more practical Model 4, the respective growth variable was “mean annual diameter increment of a tree at breast height” measured over bark during six growing seasons. Model 4 makes it easier to predict the occlusion rate of knots of different birches, because all the variables are able to be measured or predicted by using growth and branch distribution models (Mäkinen and Colin 1998, 1999; Hynynen et al. 2010). The diameter and increment variables, used as natural logarithms, were continuous independent variables in Models 3 and 4, in which four dummy variables with the values of 0(no) and 1 (yes) were also defined for prunings in spring and autumn, for living branches, and for saw pruning.
The significance of mixed effects in the ordinal regression models (Models 1 and 2) was tested using the chi-squared likelihood ratio statistic (Christiansen 2018a). If there were differences in the log-likelihoods between the fixed-effect and corresponding mixed-effect models, p values under 0.05 (in Chi2-test) showed more significant models with the random effects. In the linear mixed models (Models 3 and 4) the significance of mixed effects were evaluated based on to the covariance parameters of random effects (using restricted maximum likelihood method and assuming covariance structures with constant variances and no correlation between elements).
Also other tree- and branch-level predictors were tested as fixed effects in the formulated models. The selected fixed effects showed mostly small significance values (below 0.05 in Wald tests with ordinal linear mixed models and in F tests with linear mixed models), thus they contributed to the model. The differently formulated mixed-effect models with various dependent variables were compared with each other using the Akaike’s information criterion (AIC) (Akaike 1974).
We also tested which factors correlated with the discolouration in the stemwood observed outside the knot using Pearson correlation coefficients. Two mixed-effect models of the ordinal response data were analysed using the cumulative link mixed models (clmm) function in the ordinal package (Christensen 2018a, 2018b) in the R software (version 3.5.2) (R Core Team 2018), and the other statistical models (one regression model, bivariate correlation analysis and two linear mixed models) used the IBM SPSS 25.0 software (IBM Corp 2018).
3 Results
3.1 Knot occlusion according to visual classification
3.1.1 Evaluation from stem surface and split knot
When the progress of occlusion was visually evaluated from the stem surface, the following proportions of knots in different occlusion classes were observed: 5% unpruned branch or occlusion not started, 14% visible knot stub, 22% occlusion underway but wound still open, 19% wound closed but visible, and 41% scar visible but wound not visible. In the earliest saw and secateurs prunings (19 March, 29 April, or 3 June) 83–91% of knots were fully occluded. Also, for saw pruning on 15 July, two thirds of the knots were occluded, whereas late summer and autumn pruning resulted in the knot occlusion of only 40–50%. In the case of stick pruning, occlusion was started in approximately 50% and the wound was closed for 46% of the knots.
When occlusion was internally classified from images of the split knots, as much as 45% of the studied knots were completely occluded, and one third of these were occluded without any discolouration (Table 5). The spring pruned trees had the highest proportion of occluded knots (72% of all knots) compared with the corresponding proportions in the summer and autumn pruned trees (39% and 35% of all knots, respectively). In the stick pruned trees, 42% of knots were occluded.
There were only a few knots without any signs of occlusion in spring pruned trees, whereas summer and autumn pruned trees had 15 and 22% of such knots, respectively. Almost half of the stick pruned knots showed no signs of occlusion. Only a few knots had been occluded in unpruned control trees during the study period, which is a result of the slow rate of self-pruning.
The external assessment of occlusion was compared with the internal one. Approximately three out of four external estimates corresponded with the internal classification from split knots. In cases where the knot stub was still visible on the stem surface, occlusion had started in 25% of the knots, mostly from the upside of the knot. The external grading was, in general, more optimistic than the internal reality indicating less complete occlusion. A total of 16% of the knots that were externally assessed as the class “scar visible but wound not visible” turned out to be only partially occluded when the knots were split. For the external class “wound closed but visible” this percentage was 40%.
3.1.2 Effect of pruning date on internal occlusion classes
When the effect of the pruning date on the internal occlusion rate was tested in case of eight secateur prunings, the knots pruned at the earliest date on 19 March occluded significantly faster than the knots of the later pruning dates according to Model 1. Lower parameter estimates in Model 1 indicate higher knot occlusion rates (Table 6). The most advanced occlusion classes were more frequent with thin branches in fast-growing birch trees pruned in early spring. Interestingly, branches that were pruned alive occluded more efficiently than the ones pruned as dead. The decrease in vitality from living to dead corresponds to an increase of 2.5 mm in the branch diameter or a decrease of 2.6 mm in the cumulative radial increment of the tree at the height of a branch. Model 1 with the random stand and tree effects performed better (AIC = 2859, Chi2 = 78.8, df = 2, p < 0.0001) than the model without them (AIC = 2933).
| Table 6. Parameter estimates and standard errors (S.E) of the ordinal regression model with mixed effects (Model 1) predicting the probability of an internally evaluated occlusion class (categories 1–6 in Table 5) for a branch pruned by secateurs at eight alternative dates (N = 1000). | ||||
| MODEL 1 | ||||
| Threshold coefficients | Estimate | S.E. | z value | |
| Occlusion classes 1|2 | –1.3515 | 0.721 | –1.874 | |
| Occlusion classes 2|3 | 0.6887 | 0.722 | 0.955 | |
| Occlusion classes 3|4 | 1.9124 | 0.723 | 2.644 | |
| Occlusion classes 4|5 | 3.7859 | 0.730 | 5.183 | |
| Occlusion classes 5|6 | 5.2673 | 0.744 | 7.078 | |
| Parameter | Estimate | S.E. | z value | Sig. |
| Horizontal diameter of a branch, mm | 0.1689 | 0.019 | 8.830 | <0.001 |
| Cumulative net radial increment over bark in 5–6 years, mm | –0.1644 | 0.029 | –5.597 | <0.001 |
| Treatment (ref. secateurs 19.3.) | ||||
| - secateurs 29.4. | 0.9643 | 0.442 | 2.181 | 0.029 |
| - secateurs 3.6. | 1.0562 | 0.443 | 2.387 | 0.017 |
| - secateurs 23.6. | 2.1187 | 0.447 | 4.744 | <0.001 |
| - secateurs 15.7. | 2.2457 | 0.468 | 4.796 | <0.001 |
| - secateurs 5.8. | 2.0378 | 0.452 | 4.508 | <0.001 |
| - secateurs 26.8. | 2.5737 | 0.457 | 5.629 | <0.001 |
| - secateurs 16.9. | 1.8757 | 0.450 | 4.171 | <0.001 |
| Vitality of a branch (ref. living branch) | ||||
| - dead branch | 0.4315 | 0.140 | 3.081 | 0.002 |
| Random part | Variance | SD | ||
| Stand effect (δstand2) (N = 4) | 0.1276 | 0.3572 | ||
| Sample tree effect (δtree2) (N = 64) | 0.5421 | 0.7363 | ||
Fig. 2 illustrates the results of Model 1, presenting how the timing of secateurs pruning affects the occlusion of a 15-mm diameter knot cut as a living branch in trees with 18-mm cumulative radial growth during five to six years after pruning. According to Model 1, the stub of a living branch would clearly occlude quicker after spring pruning than a similar knot after summer or autumn pruning. The probabilities for the complete occlusion of 15-mm diameter knots after spring pruning are 75, 54 and 51% on the pruning dates of 19 March, 29 April, and 3 June, respectively. When cut later in summer or autumn, similar knots would occlude completely during the study period only with probabilities of 19–32%, depending on the pruning time. According to Model 1, knots pruned by secateur on 26 August achieved the lowest probability for the complete occlusion.
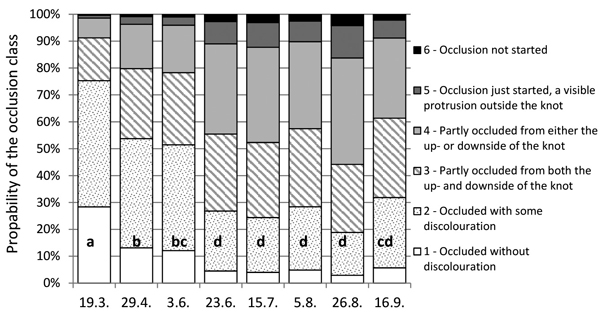
Fig. 2. Effect of the pruning date on the occlusion of 15-mm thick secateurs-pruned living branches with the cumulative 18-mm net radial growth (over bark at the branch height) according to Model 1. Percentage bars illustrate the probabilities of these branches pruned at eight alternative dates to fall into different occlusion classes. The same letter (a, b, c or d) in the bars indicates an insignificant difference (p > 0.05) in the occlusion between the pruning dates.
Fig. 3 demonstrates how the branch diameter and the radial growth of a tree affect the occlusion of the knot cut as a living branch by secateurs in summer according to Model 1. The thinner the branch and the wider the radial growth of a tree, the quicker was the occlusion. For example, if the net radial increment of the tree within half a decade is 10 mm, a 10-mm diameter knot occluded with a 17% probability, but if the net radial increment is 30 mm, the probability to occlude for the similar knot is 84%. If the branch is 25 mm thick, the probabilities for complete occlusion in the case of 10- and 30-mm net cumulative radial increment trees are 2% and 30%, respectively.
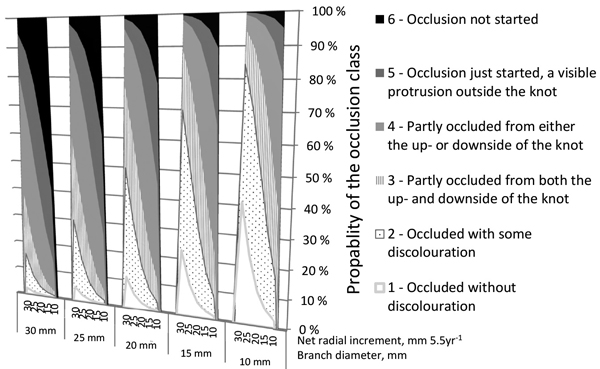
Fig. 3. Effects of the horizontal diameter of a branch (mm) and the cumulative net radial increment over bark (mm) of a tree (at the height of the branch) on the estimated probabilities of occlusion classes in the case of living branches pruned with secateurs on 15 July, according to Model 1. The percentage characterizes the probability of a branch to fall into a certain occlusion class.
3.1.3 Effect of pruning method and season on internal occlusion classes
The effect of the pruning method on the occlusion class of knots was also studied using the evaluations for secateurs, saw, and stick pruned branches and unpruned control branches (Table 5). According to Model 2 (Table 7), the occlusion process was at its fastest in the case of knots pruned by secateurs or saw in the spring, and at this time the two methods did not differ from each other in terms of the occlusion classes (p = 0.982). Occlusion slowed down in knots pruned by both saw and secateurs in summer or autumn compared to spring pruning (p < 0.03) except saw pruning in summer (p = 0.123). Saw pruned knots occluded faster than similar knots pruned with secateurs later in summer or in autumn. An increase of 1.2 mm in the branch diameter would delay the occlusion of pruned knots nearly as much as a decrease of 1 mm in the cumulative net radial increment of the tree. Model 2 with the random stand and tree effects performed better (AIC = 2863, Chi2 = 120.63, df = 2, p < 0.0001) than the model without them (AIC = 2980).
| Table 7. Parameter estimates and standard errors (S.E.) of the ordinal regression model (Model 2) with mixed-effects predicting the internally evaluated occlusion class (categories 1–8 in Table 5) for a branch pruned by saw, secateurs, or stick or unpruned (control) (N = 1001). | ||||
| MODEL 2 | ||||
| Threshold coefficients | Estimate | S.E. | z value | |
| Occlusion classes 1|2 | –1.8186 | 0.835 | –2.179 | |
| Occlusion classes 2|3 | 0.3571 | 0.835 | 0.428 | |
| Occlusion classes 3|4 | 1.5259 | 0.837 | 1.823 | |
| Occlusion classes 4|5 | 2.5602 | 0.838 | 3.054 | |
| Occlusion classes 5|6 | 3.4792 | 0.842 | 4.134 | |
| Occlusion classes 6|7 | 6.3755 | 0.907 | 7.032 | |
| Occlusion classes 7|8 | 12.0251 | 1.115 | 10.782 | |
| Parameter | Estimate | S.E. | z value | Sig. |
| Horizontal diameter of a branch, mm | 0.1158 | 0.018 | 6.279 | <0.001 |
| Cumulative net radial increment over bark in 5–6 years, mm | –0.1381 | 0.035 | –3.935 | <0.001 |
| Treatment (ref. secateurs 19.3.) | ||||
| - saw 19.3. | –0.0129 | 0.577 | –0.022 | 0.982 |
| - secateurs 15.7. | 1.9503 | 0.602 | 3.242 | 0.001 |
| - saw 15.7. | 0.8946 | 0.580 | 1.543 | 0.123 |
| - secateurs 26.8. | 2.1518 | 0.584 | 3.684 | <0.001 |
| - saw 26.8. | 1.3180 | 0.599 | 2.200 | 0.028 |
| - stick in autumn 2004 | 2.1664 | 0.617 | 3.513 | <0.001 |
| - stick in spring 2005 | 2.7407 | 0.620 | 4.418 | <0.001 |
| - no pruning (control) | 10.1923 | 0.786 | 12.968 | <0.001 |
| Random part | Variance | SD | ||
| Stand effect (δstand2) (N = 4) | 0.1813 | 0.426 | ||
| Sample tree effect (δtree2) (N = 72) | 1.0877 | 1.043 | ||
Model 2 also estimates remarkably slower occlusion for stick pruned knots than for saw and secateurs pruned knots (Fig. 4). When a 15-mm diameter knot (in a tree with an 18-mm cumulative radial growth) pruned by stick would be completely occluded with a probability of 16–26% after five growing seasons, the corresponding probabilities are 45–75% in saw pruning and 26–75% in secateurs pruning, depending on the pruning time.
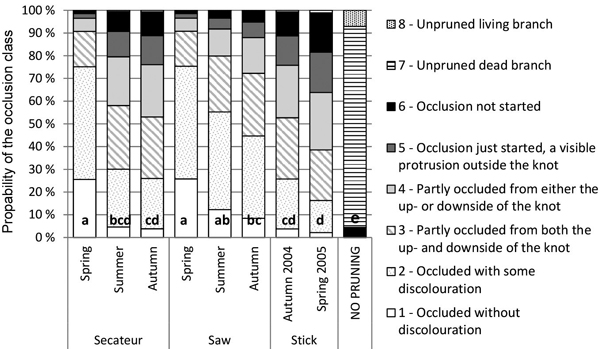
Fig. 4. Effects of the pruning method and timing on the occlusion of 15-mm thick branches with the cumulative 18-mm net radial growth (over bark at the branch height) according to Model 2. The percentage bars illustrate the probabilities of these branches to fall into different occlusion classes. The same letter (a, b, c, d or e) in the bars indicates an insignificant difference in (p > 0.05) the occlusion between the treatments.
3.2 Measured occlusion percentage of a knot
Table 8 presents the means and standard deviations of occlusion percentages for stubs of living, dead, and all knots in three saw prunings and eight secateurs prunings on different dates. Measurements from cross-cut surfaces of longitudinally split knots showed that the average occlusion percentages were 72 and 65% for branches pruned as living or dead, respectively. The highest average occlusion rate (95%) for stubs of living branches was observed in the case of secateurs pruning on 19 March, and the lowest rate (40%) for dead knots in the case of secateurs pruning was on 15 July. Ten knots (belonging to occlusion classes 3–5 in Table 5) were not able to be measured and were excluded from this analysis.
| Table 8. Numbers (N) and mean occlusion percentages with standard deviations (SD) of studied branches pruned by secateurs (Sc) and saw (Sw) at different dates during the growing season in 2004. Occlusion percentages for branches were evaluated five to six years after pruning. | ||||||||||||
| Pruning method and date | ||||||||||||
| Sc | Sw | Sc | Sc | Sc | Sc | Sw | Sc | Sc | Sw | Sc | ALL | |
| 19.3. | 19.3. | 29.4. | 3.6. | 23.6. | 15.7. | 15.7. | 5.8. | 26.8. | 26.8. | 16.9. | ||
| Living branches | ||||||||||||
| N | 42 | 37 | 68 | 78 | 54 | 51 | 68 | 67 | 47 | 36 | 44 | 592 |
| Mean percentage | 95.0 | 90.3 | 85.3 | 86.8 | 72.3 | 61.4 | 79.6 | 50.2 | 48.0 | 60.4 | 61.1 | 72.4 |
| SD | 15.3 | 23.2 | 23.3 | 24.2 | 32.4 | 30.7 | 32.1 | 31.3 | 38.6 | 39.7 | 34.5 | 33.5 |
| Dead branches | ||||||||||||
| N | 101 | 79 | 57 | 52 | 70 | 64 | 57 | 58 | 48 | 77 | 79 | 742 |
| Mean percentage | 88.8 | 88.8 | 74.9 | 87.3 | 46.5 | 40.3 | 69.8 | 58.0 | 50.9 | 53.5 | 49.4 | 65.3 |
| SD | 23.4 | 24.7 | 33.0 | 23.1 | 40.1 | 40.3 | 40.7 | 39.7 | 42.8 | 40.8 | 43.0 | 40.0 |
| All branches | ||||||||||||
| N | 143 | 116 | 125 | 130 | 124 | 115 | 125 | 125 | 95 | 113 | 123 | 1334 |
| Mean percentage | 90.6 | 89.3 | 80.6 | 87.0 | 57.7 | 49.7 | 75.1 | 53.8 | 49.4 | 55.7 | 53.6 | 68.4 |
| SD | 21.4 | 24.1 | 28.5 | 23.7 | 39.0 | 37.7 | 36.4 | 35.5 | 40.6 | 40.4 | 40.4 | 37.4 |
Two alternative models with different growth variables were formulated to predict the occlusion percentages for saw and secateurs pruned knots. Although the difference of growth variables, the functioning (i.e., coefficients for predictor variables) in Models 3 and 4 was near to each other (Table 9). In the models, negative values for predictor estimates indicate slower and positive values indicate faster occlusion of a knot. Also according to the models, spring pruning accelerates and autumn pruning delays the occlusion process, but in Model 3 occlusion rates in autumn prunings were not significantly differed from those in summer prunings (p = 0.114). Also, a knot pruned with secateurs occludes slower than a knot pruned by saw. Lower occlusion rates are estimated by Models 3 and 4 for thicker knots in slow-grown trees than for thinner knots in fast-grown trees, which is logical. Moreover, knot occlusion slightly accelerated with the increasing height of a branch on the stem. The causal-like Model 3 (AIC = 1491) explained the occlusion rate of a knot (exactly, the arcsine transformation of that) almost as well as the prediction Model 4 (AIC = 1490).
| Table 9. Parameter estimates and standard errors (S.E.) for Models 3 and 4 to estimate the arcsine transformation of the occlusion rate (0–1) for a saw or secateurs pruned branch (N = 1334). AIC = Akaike’s information criterion. | ||||||
| MODEL 3 | MODEL 4 | |||||
| Parameter | Estimate | S.E. | Sig. | Estimate | S.E. | Sig. |
| Fixed part | ||||||
| Intercept | 0.30398 | 0.30378 | 0.3188 | 1.09016 | 0.20446 | <0.001 |
| Vitality of a branch (ref. dead) | ||||||
| - living | 0.08389 | 0.02800 | 0.0028 | 0.08189 | 0.02800 | 0.004 |
| Pruning method (ref. saw) | ||||||
| - secateurs | –0.25935 | 0.05614 | <0.001 | –0.27642 | 0.05785 | <0.001 |
| Pruning in spring (ref. no) | ||||||
| - yes | 0.31139 | 0.06044 | <0.001 | 0.38542 | 0.05958 | <0.001 |
| Pruning in autumn (ref. no) | ||||||
| - yes | –0.10047 | 0.06293 | 0.1144 | –0.14228 | 0.06505 | 0.032 |
| Ln(vertical diameter of a branch, mm) | –0.53603 | 0.03541 | <0.001 | –0.53061 | 0.03538 | <0.001 |
| Ln(cumulative net radial increment over bark, mm) | 0.72287 | 0.10672 | <0.001 | |||
| Ln(dbh increment over bark, mm a–1) | 0.69200 | 0.10401 | <0.001 | |||
| Height of a branch, dm | 0.00707 | 0.00132 | <0.001 | 0.00967 | 0.00127 | <0.001 |
| Random part | ||||||
| Random error (δe2) | 0.15580 | 0.00626 | 0.15516 | 0.00623 | ||
| Stand effect (δstand2) (N = 4) | 0.00596 | 0.00767 | 0.00668 | 0.00810 | ||
| Sample tree effect (δtree2) (N = 88) | 0.04245 | 0.00859 | 0.04519 | 0.00895 | ||
| AIC | 1491 | 1490 | ||||
Fig. 5 illustrates the occlusion percentages for secateurs spring pruned living and dead branches with alternative branch diameters and radial increments, according to Model 3. If the cumulative radial increment of a tree during six growing seasons is at least 35 mm at the branch height, the whole gap (wound) of a knot with the diameter of 20 mm or less will be occluded in six years. In moderate-growing trees (with the radial increment of 20 mm in six years), the wound of a small knot (diameter < 10 mm) will be occluded, but in the case of 20 and 30 mm knots, only 70% and 40−50% of the knot diameter will be closed, respectively.
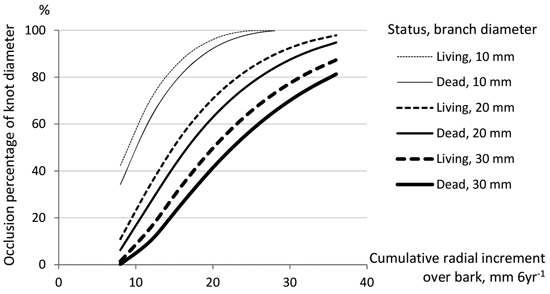
Fig. 5. Occlusion percentages (% of branch diameter) estimated by Model 3 for living and dead branches pruned by secateurs in spring according to the vertical diameter of a branch and the cumulative radial increment of a stem at the branch height of 25 dm (during six growing seasons after pruning, good occlusion rate).
Fig. 6 demonstrates how the pruning method (saw or secateurs) and the branch diameter affect the occlusion rates of stubs of living branches after summer pruning, according to Model 3. When the cumulative radial increment was 35 mm after pruning, the wound of a 20-mm diameter living branch is just closed if pruned by saw, but approximately 20% of the respective wound of the secateurs pruned knot is still open. In slow-growing trees (with the cumulative radial increment of 10 mm after pruning), occlusion would progress slowly, especially on secateurs pruned knots in which 0–40% of a diameter is closed, depending on the knot diameter. In slow-growing trees pruned with a saw, one third of a wound is still open in the case of living branches with a diameter of 10 mm.
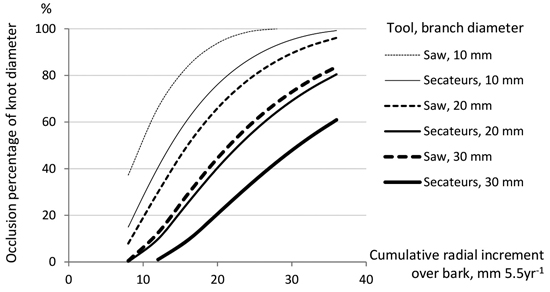
Fig. 6. Occlusion percentages (% of branch diameter) estimated by Model 3 for living branches pruned by saw or secateurs in summer according to the vertical diameter of a branch and the cumulative radial increment of a stem at the branch height of 25 dm (during five and a half growing seasons after pruning, moderate occlusion rate).
3.3 Discolouration in the stemwood
A total of 33% of the studied knots (N = 1585) indicated some kind of discolouration upwards or/and downwards from the knot five to six years after the pruning. Discolouration was more typical upwards (32% of knots) than downwards (12%).
In order to present pruning-induced discolouration, Table 10 includes the average discolouration percentages of living, dead, and all branches pruned with different tools and dates. Discolouration in the stemwood was more common in the case of dead (43% of knots discoloured) than living branches (21%), but the variation between pruning treatments was high. Discolouration in the stemwood was observed in 22% of the studied knots in unpruned reference trees and in 25% of the studied knots in stick pruned trees, but the discolouration percentages were remarkably higher in secateurs and saw pruned trees, 35 and 39%, respectively.
| Table 10. Proportions of discoloured knot samples and mean spreading distances of stemwood discolouration (with standard deviations, SD) for different pruning treatments. The results are presented for living, dead, and all branches five to six growing seasons after pruning based on measurements from the images of split knots (N = 1585). Some samples were rejected due to large colour defects in the stemwood caused by unknown defects. | ||||||||
| Pruning method | Pruning date | Discoloured, % of samples | Mean spreading distance (SD), mm | Reject samples | ||||
| Living | Dead | All | Living | Dead | All | |||
| Secateurs | 19.3. | 31.7 | 48.5 | 43.6 | 40.6 (28.2) | 35.2 (20.8) | 36.3 (22.4) | 6 |
| Saw | 19.3. | 44.4 | 45.2 | 45.0 | 30.5 (23.0) | 26.1 (23.4) | 27.6 (23.1) | 10 |
| Secateurs | 29.4. | 14.7 | 32.2 | 22.8 | 41.1 (28.9) | 22.5 (19.4) | 28.9 (24.3) | 2 |
| Secateurs | 3.6. | 15.4 | 44.2 | 26.9 | 15.0 (9.2) | 13.5 (9.4) | 14.0 (9.2) | 1 |
| Secateurs | 23.6. | 14.5 | 47.8 | 32.8 | 16.3 (16.4) | 32.8 (23.9) | 29.5 (23.3) | 6 |
| Secateurs | 15.7. | 16.7 | 44.6 | 31.9 | 18.8 (11.8) | 15.2 (14.3) | 16.1 (13.6) | 0 |
| Saw | 15.7. | 22.1 | 48.2 | 33.9 | 15.5 (13.3) | 17.8 (13.5) | 17.0 (13.3) | 1 |
| Secateurs | 5.8. | 20.9 | 51.7 | 35.2 | 19.1 (20.8) | 26.0 (16.4) | 23.8 (18.0) | 0 |
| Secateurs | 26.8. | 10.0 | 40.0 | 24.2 | 22.8 (29.6) | 19.8 (13.4) | 20.5 (17.3) | 4 |
| Saw | 26.8. | 35.3 | 40.8 | 39.0 | 22.7 (21.6) | 24.6 (23.4) | 24.1 (22.6) | 9 |
| Secateurs | 16.9. | 37.2 | 72.5 | 58.9 | 15.4 (11.9) | 25.1 (20.0) | 22.8 (18.8) | 11 |
| Stick 1) | autumn 2004 | - | 36.8 | - | - | 19.7 (17.0) | - | 2 |
| Stick 1) | spring 2005 | - | 27.1 | - | - | 16.9 (14.1) | - | 0 |
| Control | not pruned | 19.4 | 22.5 | 21.6 | 32.8 (13.3) | 21.1 (17.0) | 24.4 (16.7) | 0 |
| ALL | 21.7 | 42.6 | 34.3 | 23.8 (21.2) | 23.8 (18.1) | 23.8 (19.9) | 52 | |
| 1) Living branches were not removed in stick pruning. | ||||||||
Discolouration in the stemwood was noticed most often in the earliest and latest saw prunings, i.e., 19 March (45% of knots) and 26 August (39% of knots) and, similarly, in the earliest and latest secateurs prunings on 19 March (44% of knots) and 16 September (59% of knots). The lowest proportions of discolouration were 10% for living branches pruned with secateurs on 26 August and 32% for dead branches pruned with secateurs on 29 April.
Table 10 shows the mean colour spreading distances (maximum distances measured upwards or downwards) for living, dead, and all branches pruned by different treatments, based on the measurements of the knot samples in which some kind of discolouration in the stemwood was observed. The average colour spreading distances were 24 mm for both living and dead branches. The lowest distances (14 mm on average) were measured in the samples of dead branches pruned with secateurs on 3 June, and the highest (41 mm on average) in the samples of living branches pruned with secateurs on 29 April.
Based on bivariate correlations, the vertical diameter of the branch increased the probability for discolouration in the stemwood (r = 0.063, p < 0.012, N = 1585). Also, if the branch was dead at the time of pruning, its probability of spreading discolouration increased (r = 0.215, p < 0.001). The branch height (r = –0.203, p < 0.001) and cumulative radial increment of the tree had a lowering effect on the discolouration (r = –0.087, p = 0.001). No difference was observed in the relative proportions of discoloured knots between pruned and unpruned control trees (r = 0.019, p = 0.456). Thus, pruning, per se, did not increase the proportion of discoloured knots.
One third of all completely occluded study knots (766 in Table 5) were without any discolouration outwards from the branch stub (Fig. 1). In the rest two thirds of the cases, the average spreading distance of discoloured callus outwards from the stub end was 4.3 mm (SD 2.7 mm).
4 Discussion
4.1 Validity, reliability, and representativeness
The effects of different pruning methods and dates were analysed in this study near the time of the first commercial thinning according to the prevailing Finnish practice. Only a few comparable results from controlled birch pruning experiments have been reported: Rintala (1995) and Verkasalo and Rintala (1998) studied pruning dates, Schatz et al. (2008) studied pruning by secateurs and saw, and Wang et al. (2017) studied occlusion of different knots. A novel approach in this study was the branch-level modelling of occlusion rates. Our material consisted of knots identified and measured in both the pruning and analysis phases with reliable data regarding the locations, diameters, and vitality of the branches at the time of pruning.
Analysing the knots five to six years after pruning turned out to be excellent timing with large diversion in the occlusion detected with different tree growth, branch viability, knot diameter, and pruning dates or methods. In the best cases (early spring pruning) as much as 75% of the pruned knots had been completely occluded, whereas in the worst cases the percentage was only 15–20%. The process of self-pruning was still ongoing in the unpruned control trees.
The pruning experiment was carried out in four planted silver birch stands on fertile sites. Only good quality dominant trees were accepted for pruning. The mean dbh (7.3–10.2 cm) and dominant height (9.6–12.2 m) of the study stands in the pruning stage and the respective annual growths (5.0–6.3 mm and 5.5–10.2 cm) are in line with previous findings for silver birch on forest and agricultural land (Heiskanen 1957, 1966a; Raulo 1977, 1979; Oikarinen 1983; Anttonen 1990; Valkonen 1992; Niemistö 1995a, 1995b; Niemistö et al. 1997). According to Oikarinen (1983) and Niemistö (1997), the basal area-weighted dbh increments in planted silver birch stands at a similar development stage were 5.0–6.0 and 3.5–6.0 mm a–1, respectively. Raulo (1977) stated that the diameter and height increments can be as high as 10 mm a–1 and 100 cm a–1 in fast growing silver birch trees, respectively. Thus, the tree sizes and growth rates in this study were sufficient to generalize the results for planted silver birch stands in Finland.
The variation in mean diameters of study branches between different treatments was 7.8–15.9 mm for dead and 12.8–19.6 mm for living branches. The diameter of the branches was similar than in previous findings (Raulo 1979; Niemistö 1997; Verkasalo and Rintala 1998). The branchiness of the study trees can, thus, be regarded as representative for stems selected to pruning in planted birch stands in Finland. Our stand data consisted mainly of birch trees with branches below 25 mm in diameter.
4.2 Occlusion rate of study knots
Along with the pruned branch stub length and radial growth of the tree, the diameter of a pruned branch is an important factor influencing the time needed for the occlusion of a knot independent of the tree species (Verkasalo and Rintala 1998; DeBell et al. 2006; Kannisto and Heräjärvi 2006; Hein and Spiecker 2007; Hein 2008; Dănescu et al. 2015; Wang et al. 2015, 2016; Sheppard et al. 2016; Stener et al. 2017). According to our study, approximately 70–80% of the diameter of an average knot stub was covered in birch trees with the average growth rate in five to six years. Small knots in fast grown trees were completely occluded, but occlusion was just initiating in large knots of slow-growing trees. Verkasalo and Rintala (1998) noticed that 70% of small knot stubs (diameter < 10 mm) and 20% of large knots (>20 mm) were occluded five to six years after pruning. According to Stener et al. (2017), 87–91% of the pruned knots were covered by new wood ten years after pruning. Schatz et al. (2008) stated that pruned knots with the diameter less than 20 mm occlude within five to eight years, which corresponds with the findings of this study. The model by Dănescu et al. (2015) for Acer pseudoplatanus L. and Fraxinus excelsior L. predicted shorter occlusion duration of knots 10–30 mm in diameter, only two to three years. Especially in natural pruning, the dead branch stub length plays also an important role in predicting branch occlusion times (Dănescu et al. 2015; Wang et al. 2016).
Verkasalo and Rintala (1998) reported that occlusion was faster in cases where the trees were pruned in early or middle summer in comparison to spring and autumn pruning. Dănescu et al. (2015) did not notice any difference between March and June prunings in maple or ash. This contradicts with this study, in which spring pruning from March to the beginning of June accelerated the occlusion process compared to pruning in midsummer or in autumn. The meristem is most active early in the growing season, which supports initiation of rapid occlusion. According to the recent finding of Miyshima et al. (2019), procambial development during the early growing season forms a foundation for further radial growth during the growing season. This supports our finding that suggests faster occlusion for branches that are pruned before or during the start of the cambial activity, i.e., from spring to early summer.
The main pruning tools in this study were secateurs and saws. Unexpectedly, the stubs of saw pruned knots occluded faster than the same sized ones pruned with secateurs. Schatz et al. (2008) did not notice any differences in stub occlusion speed between pruning tools. Apparently, the reason for this finding is the length of the knot stub that turned out to be on average 3.6 mm shorter (under bark) in the saw pruned knots than in the secateurs pruned ones. Thus, based on this study, we cannot state which tool is better for pruning of birches in terms of the occlusion of a wound. Furthermore, pruning methods such as target pruning (cutting perpendicular to the branch) and flush pruning (cutting parallel to the stem) play a considerable role in the occlusion speed and spreading of colour defects (O’Hara 2007; Sheppard et al. 2016). In spite of the direction to use target pruning with a smaller knot wound in our study, the saw pruning of branches with a small insertion angle tended to be more or less close to a flush pruning, resulting in shorter knot stubs compared to secateurs pruning.
On the other hand, the study trees were pruned carefully, with special attention to the work quality. In normal forest work, not only avoidance of damage but also pruning work productivity is important. Comparisons between pruning tools should be based on a work study that takes both of these into account. If done correctly, pruning improves the quality of birch logs independent of the tool used (Heiskanen 1957; Kannisto and Heräjärvi 2006).
In this study, the occlusion class (Models 1–2) and percentage (Models 3–4) of a pruned knot were modelled on the basis of pruning season and tool. The mixed-effect models, in which the stand and sample tree were random factors, took into account the diameter of an individual pruned branch, its vertical location in the tree, the growth rate of that tree, and the vitality of the branch (living/dead). According to Model 1, the spring pruned knots (on 19 March, 29 April, and 3 June) occluded more quickly than those pruned in summer or autumn. Model 2 that contained all pruning methods confirmed the good results for spring pruning. However, spring pruned trees had time to grow six annual rings in the analyses, whereas the late summer and autumn pruned trees had five annual rings. Models 1–3 accounted for this difference by using the post-pruning five to six-year cumulative radial growth at the branch height as an explanatory variable. However, the pruning season was still a significant predictor in these models so that the spring pruning or the number of post pruning year rings (or both) have a positive effect on the knot’s occlusion rate besides the cumulative radial increment. Model 4, on the other hand, was constructed for practical needs. Therefore, its growth variable was simply the mean annual diameter increment at breast height.
4.3 Discolouration from knots in stemwood
From the viewpoint of wood uses (veneering, sawing), it is essential that the knot stub does not cause spreading of colour defects towards the stem surface after pruning. In our material, two thirds of the completely occluded knots (N = 766 knots) had spread slight colour defect towards the surface. However, this discolouration extended only some millimetres towards the surface, whereas the extension upward and downward was typically tenfold greater. Because of the relatively short period of five to six years from pruning to felling of the study trees, the completely occluded knots were mainly smaller than average ones and pruned in the springtime. Thus, based on this material, we cannot say how prone the thicker and autumn pruned knots are to spreading colour defects. Colour defects spreading from the pruned knots to the stemwood were twice as common if branches were pruned as dead than if pruned alive. Stener et al. (2017), who studied pruned birches after ten years of pruning, noticed that secateurs pruning did not increase the probability for discolouration towards stem surface. On the other hand, pruned knots spread slightly more colour defects towards the pith than the unpruned ones.
In general, every third studied knot had spread some discolouration into the stemwood. The colour defect was more often spread upward from the knot than downward, and its average length was 24 mm independent of the vitality status of the branch during pruning. In unpruned control trees colour defects were detected in the stemwood in the vicinity of 22% of the knots analysed, but the corresponding percentage was 32% in the case of stick pruned dead knots. Pruning with saw or secateurs increased the percentage of colour spreading knots up to 35%, with no difference between the two pruning tools. On the contrary, Schatz et al. (2008) noticed more common discolouration in saw pruned knots than in secateurs pruned knots 15 years after pruning. Kannisto and Heräjärvi (2006) did not notice differences in the discolouration of pruned and unpruned knots but reported more severe stemwood discolouration in the case of thicker pruned knots. Similar results were noticed by Wang et al. (2016) between natural and artificial pruning in the study of Betula alnoides Buch.-Ham. ex D. Don in China. Dănescu et al. (2015) stated that artificial pruning increased the discolouration of stemwood in ash trees, but no such differences were detected between artificial and natural pruned maple trees.
Stem discolouration depends on branch diameter, tree species, pruning season and climate conditions (Kannisto and Heräjärvi 2006; Dănescu et al. 2015; Sheppard et al. 2016; Wang et al. 2016). In the case of silver birch, only 10% of knots with a diameter less than 10 mm and approximately 50% of those with diameters over 20 mm spread colour defects (Kannisto and Heräjärvi 2006). Half of the studied knots were completely occluded in 5–6 years and two thirds of them had a discoloured callus outwards from the stub with the mean extension of 4.3 mm. This number is probably an underestimation for all knots, because the occlusion process was underway in most of the larger-sized knots.
In the case of wild cherry, Sheppard et al. (2016) concluded that a knot stub occlusion time of more than three years increases the risk of discolouration. Dănescu et al. (2015) stated that discolouration in the stemwood increased remarkably in maple when the diameter of a knot was 50 mm or more, whereas in ash this occurred already for knot diameters of 10–30 mm. They noticed also that the pruning season (late winter or summer) did not effect on the stem discolouration and branch occlusion in maple and ash trees.
There was a great and unexplained variation in the existence and spreading distance of colour defects in the stemwood. Therefore, studying the effect of pruning season on colour defects after five to six years was too early for statistical testing. This will be done later when analysing the data from the same experiment ten years after pruning. However, the first observations in this study indicate that the discolouration is more widespread in the case of knots pruned in early spring or late autumn than those pruned in summer. Verkasalo and Rintala (1998) reported the highest discolouration rates in autumn pruned knots of birches.
4.4 Applicability in forest practice
Based on the previous research results (Verkasalo and Rintala 1998; Kannisto and Heräjärvi 2006), the Finnish birch pruning recommendations have suggested that only birch trees with branches less than 20 mm diameter in the butt log section should be accepted for silvicultural pruning (Äijälä et al. 2014). The same limits for the diameter of pruned branches are applied to birch in Sweden (Stener et al. 2017). Dead knots and the associated colour defects are among the most important factors decreasing the quality of birch veneer and sawn timber (Heiskanen 1966b; Baldwin 1995; Verkasalo 1997; Heräjärvi 2002). According to this study, living branches with diameters up to 25 mm or even 30 mm occluded well during five to six years when the annual radial stem growth was 4 mm or more. However, a more detailed examination of discolouration risk is needed for the later stages of the stands in our experiment, when most of the knots will be totally occluded.
In addition to pruning, the quality of the branches in birch stands can be influenced also by the selection of the regeneration material (Viherä-Aarnio and Velling 1999; Stener and Jansson 2005), site selection (Niemistö et al. 1997), and forest management, i.e., the stand density before and after pre-commercial and commercial thinning (Niemistö 1995a, 1997; Mäkinen et al. 2003). Dense spacing in young birch stands decreases the diameter increment of branches and facilitates their suppression, death, and self-pruning (Cameron et al. 1995; Niemistö 1995a; Mäkinen 2002; Mäkinen et al. 2003; Hynynen et al. 2010; Wang et al. 2015, 2017, 2018). Delay or negligence in thinning, on the other hand, clearly slows down the self-pruning of dead branches as well as the diameter increment of the birch trees (Niemistö 1997), thus reducing the volume of knot-free wood outside the knotty core.
In this study, the branches of the unpruned control trees with an average dbh of 12 cm were dead along the future butt log but still mostly present or the occlusion process was not started. Many studies show that the natural pruning process of dead branches in the birch butt log section is a slow process, and dead branch stubs may interfere with the formation of a knot-free layer for decades (Verkasalo 1997; Hallaksela and Niemistö 1998; Heräjärvi 2001; Stener et al. 2017) or even for the entire rotation period. In birch and other broadleaves artificial pruning improves the quality and value of butt logs the more the earlier the knot-free layer starts developing over the knotty core (Hein and Spiecker 2007; Dănescu et al. 2015; Wang et al. 2016).
According to this study, the occlusion of pruned knot stubs accelerates when the diameter of the knots is small, pruned branches are alive, and the diameter increment of the tree after the pruning is fast. Therefore, we recommend concentrating on pruning fast growing stands and thin-branched young trees. Pruning is also feasible in younger stands than in this study because of higher proportion of living branches. However, pruning in one phase up to 4 m is possible only one to two years earlier than in this study, otherwise the living crown would remain too short, which compromises the tree growth. To be most efficient, stems should be pruned in two phases: at first up to 2–2.5 m when the trees are approximately five metres tall and again five to seven years later, when the trees are 10–12 m tall, the second pruning extending up to 5–6 m height. In order to ensure fast growth and rapid occlusion of pruning wounds, an initial or pre-commercial density of 1600–2000 ha–1 and a heavy first thinning at the time or soon after the completed pruning are recommended.
Although pruning facilitates the production of top quality butt logs in birch, high and medium quality logs can also be grown in a planted silver birch stand without pruning. This necessitates using breed seedling materials and dense enough spacing, applying correctly scheduled and strong enough thinning of suppressed and poor quality trees, and growing the final crop trees sufficiently large. Improving birch stem quality by conventional silvicultural means also improves the potential to have stems appropriate for pruning, since typically just the highest-quality stems are worth the pruning investment.
4.5 Needs for further research
The next steps to analyse the materials from this particular pruning experiment will reveal the effects of pruning on the diameter growth and stem form of silver birch. Furthermore, we did not analyse the pruning-induced discolouration in the stemwood in detail now, since we have a more reliable dataset available later, i.e., ten years after the initiation of the experiment. Mechanisms of discolouration, driven by access of oxygen in contact with wood material, are not fully understood.
Acknowledgements
The authors cordially thank numerous people at Finnish Forest Research Institute Metla (now Natural Resources Institute Finland Luke) for their help in field and laboratory measurements. Pekka Helminen, Lauri Hirvisaari, and Jari Ilomäki were responsibility for sample plot establishment and measurements. Tapio Järvinen, Jukka Lehtimäki, Erkki Salo, Veijo Salo, and Hannele Saloseutu measured and scanned the knots in the laboratory. We also thank Ville Hallikainen and Jari Miina for their advices in statistical modelling.
References
Äijälä O., Koistinen A., Sved J., Vanhatalo K., Väisänen P. (eds.) (2014). Metsänhoidon suositukset. [Forest management recommendations]. Metsätalouden kehittämiskeskus Tapion julkaisuja. 181 p. ISBN 978-952-6612-32-4. [In Finnish].
Akaike H. (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control 19(6): 716–723. https://doi.org/10.1109/TAC.1974.1100705.
Anttonen T. (1990). Pellolle istutettujen koivikoiden tila Pohjois-Karjalassa 79 vuoden kuluttua viljelystä. [State of birch stands planted on former agricultural land 79 years after regeneration in North Karelia]. MSc thesis on forest sciences. University of Joensuu. 50 p. [In Finnish].
Baldwin R.F. (1995). Plywood and veneer-based products. Manufacturing practices. Forest Products Society, Madison, Wisconsin. 388 p.
Cameron A.D., Dunham R.A., Petty J.A. (1995). The effects of heavy thinning on stem quality and timber properties of silver birch (Betula pendula Roth). Forestry 68(3): 275–285. https://doi.org/10.1093/forestry/68.3.275.
Christensen R.H.B. (2018a). Ordinal–regression models for ordinal data, R package version 2018.8-25. http://www.cran.r-project.org/package=ordinal/. [Cited 17 Jan 2019].
Christensen R.H.B. (2018b). Cumulative link models for ordinal regression with the R package ordinal. https://cran.r-project.org/web/packages/ordinal/vignettes/clm_article.pdf. [Cited 17 Jan 2019].
Dănescu A., Ehring A., Bauhus J., Albrecht A., Hein S. (2015). Modelling discoloration and duration of branch occlusion following green pruning in Acer pseudoplatanus and Fraxinus excelsior. Forest Ecology and Management 335: 87–98. https://doi.org/10.1016/j.foreco.2014.09.027.
DeBell D.S., Harrington C.A., Gartner B.L., Singleton R. (2006). Time and distance to clear wood in pruned red alder saplings. In: Deal L., Harrington C.A. (eds.). Red alder: a state of knowledge. General Technical Report PNW-GTR-669. U.S. Department of Agriculture, Forest Service, Pacific Northwest Research Station, Portland, Oregon. p. 103–114.
Hallaksela A.-M., Niemistö P. (1998). Stem discoloration of planted silver birch. Scandinavian Journal of Forest Research 13(2): 169–176. https://doi.org/10.1080/02827589809382973.
Hanley D.P., Oliver C.D., Maguire D.A., Briggs D.G., Fight R.D. (1995). Forest pruning and wood quality of western North American conifers. Contribution No. 77. Institute of Forest Resources. College of Forest Resources, University of Washington, Seattle, Washington. 403 p.
Hein S. (2008). Knot attributes and occlusion of naturally pruned branches of Fagus sylvatica. Forest Ecology and Management 256(12): 2046–2057. https://doi.org/10.1016/j.foreco.2008.07.033.
Hein S., Spiecker H. (2007). Comparative analysis of occluded branch characteristics for Fraxinus excelsior and Acer pseudoplatanus with natural- and artificial pruning. Canadian Journal of Forest Science 37(8): 1414–1426. https://doi.org/10.1139/X06-308.
Heiskanen V. (1957). Raudus- ja hieskoivun laatu eri kasvupaikoilla. [Quality of the common birch and the white birch on different sites]. Communicationes Instituti Forestalis Fenniae 48(6). 99 p. http://urn.fi/URN:NBN:fi-metla-201207171080. [In Finnish with English summary].
Heiskanen V. (1958). Tutkimuksia koivun karsimisesta. [Studies on pruning of birch]. Communicationes Instituti Forestalis Fenniae 49(3). 68 p. http://urn.fi/URN:NBN:fi-metla-201207171081.
Heiskanen V. (1963). Aikatutkimuksia koivun karsimisesta. [Time studies on the pruning of birch]. Silva Fennica 155(6): 1–24. https://doi.org/10.14214/sf.a14279. [In Finnish with English summary].
Heiskanen V. (1966a). Tutkimuksia rauduskoivikon karsimisen kannattavuudesta. [Studies on the profitability on pruning of common birch (Betula Verrucosa) stands]. Acta Forestalia Fennica 81(2): 1–32. https://doi.org/10.14214/aff.7167. [In Finnish with English summary].
Heiskanen V. (1966b). Tutkimuksia koivujen vikaisuuksista, niiden vaikutuksesta sorvaustulokseen sekä niiden huomioonottamisesta laatuluokituksesssa. [Studies on the defects of birch, their influence on the quality and quantity on the rotary cut veneer, and their consideration in veneer birch grading]. Acta Forestalia Fennica 80(3):1–128. https://doi.org/10.14214/aff.7165. [In Finnish with English summary].
Heräjärvi H. (2001). Technical properties of mature birch (Betula pendula and B. pubescens) for saw milling in Finland. Silva Fennica 35(4): 469–485. https://doi.org/10.14214/sf.581.
Heräjärvi H. (2002). Modelling of internal knot characteristics of mature Finnish Betula pendula and Betula pubescens. In: IUFRO Fourth Workshop, Connection between Forest Resources and Wood Quality: Modelling Approaches and Simulation Software. Harrison Hot Springs, Canada. p. 85–93.
Holopainen V.E. (1949). Karsimisen vaikutuksesta vanerikoivun kantohintaan. [Influence of pruning on the stump price of veneer log birch]. Metsätaloudellinen aikakauslehti 66(12): 415–416. [In Finnish].
Hynynen J., Niemistö P., Viherä-Aarnio A., Brunner A., Hein S., Velling P. (2010). Silviculture of birch (Betula pendula Roth and Betula pubescens Ehrh.) in northern Europe. Forestry 83(1): 103–119. https://doi.org/10.1093/forestry/cpp035.
Hytönen J., Saramäki J., Niemistö P. (2014). Growth, stem quality and nutritional status of Betula pendula and Betula pubescens in pure stands and mixtures. Scandinavian Journal of Forest Research 29(1): 1–11. https://doi.org/10.1080/02827581.2013.838300.
Kannisto K., Heräjärvi H. (2006). Rauduskoivun pystykarsinta oksasaksilla – vaikutus puun laatuun ja taloudelliseen tuottoon. [Birch pruning with secateurs – impact on wood quality and economic return]. Metsätieteen aikakauskirja 4/2006: 491–505. https://doi.org/10.14214/ma.6316. [In Finnish].
IBM Corp. (2018). IBM SPSS Statistics for Windows, Version 25.0. IBM Corp., Armonk, NY. https://www.ibm.com/support/knowledgecenter/en/SSLVMB_25.0.0/. [Cited 17 Jan 2019].
Laitakari E. (1937). Laatupuun kasvattamisesta. [Production of good quality timber]. Silva Fennica 39: 259–270. https://doi.org/10.14214/sf.a13910. [In Finnish].
Lappi-Seppälä M. (1934). Karsimisesta ja sen metsänhoidollisesta merkityksestä. [The silvicultural influences of pruning]. Acta Forestalia Fennica 40(25): 605–618. https://doi.org/10.14214/aff.7302. [In Finnish with English summary].
Lehonkoski N. (1949). Vanerikoivujemme nykyinen laatu. [Present quality of veneer log birches]. Metsätaloudellinen aikakauslehti 66: 16–19. [In Finnish].
Mäkinen H. (2002). Effect of stand density on the branch development of silver birch (Betula pendula Roth) in central Finland. Trees 16: 346–353. https://doi.org/10.1007/s00468-002-0162-x.
Mäkinen H., Ojansuu R., Niemistö P. (2003). Predicting external branch characteristics of planted silver birch (Betula pendula Roth) on the basis of routine stand and tree measurements. Forest Science 49(2): 301–317.
Mäkinen H., Colin F. (1998). Predicting branch angle and branch diameter of Scots pine from usual tree measurements and stand structural information. Canadian Journal of Forest Research 28(11): 1686–1696. https://doi.org/10.1139/x98-141.
Mäkinen H., Colin F. (1999). Predicting the number, death, and selfpruning of branches in Scots pine. Canadian Journal of Forest Research 29(8): 1225–1236. https://doi.org/10.1139/x99-065.
McCullagh P. (1980). Regression models for ordinal data. Journal of the Royal Statistical Society. Series B (Methodological) 42(2): 109–142. https://www.jstor.org/stable/2984952.
Miyashima S., Roszak P., Sevilem I., Toyokura K., Blob B., Heo J., Mellor N., Help-Rinta-Rahko H., Otero S., Smet W., Boekschoten M., Hooivel G., Hashimoto K., Smetana O., Siligato R., Wallner E.-S., Mähönen A.P., Kondo Y., Melnyk C.W., Greb T., Nakajima K., Sozzani R., Bishopp A., De Rybel A., Helariutta Y. (2019). Mobile PEAR transcription factors integrate positional cues to prime cambial growth. Nature 565: 490–494. https://doi.org/10.1038/s41586-018-0839-y.
Nicolescu N.-V. (1999). Artificial pruning – a review. Unpublished mimeograph. Brasov, Romania. 65 p.
Niemistö P. (1995a). Influence of initial spacing and row-to-row distance on the crown and branch properties and taper of silver birch (Betula pendula). Scandinavian Journal of Forest Research 10(1–4): 235–244. https://doi.org/10.1080/02827589509382889.
Niemistö P. (1995b). Influence of initial spacing and row-to-row distance on the growth and yield of silver birch (Betula pendula). Scandinavian Journal of Forest Research 10 (1–4): 245–255. https://doi.org/10.1080/02827589509382890.
Niemistö P. (1997). Ensiharvennuksen ajankohdan ja voimakkuuden vaikutus istutetun rauduskoivikon kasvuun ja tuotokseen. [Effect of the timing and intensity of first thinning on the growth and yield of silver birch]. Metsätieteen aikakauskirja – Folia Forestalia 4/1997: 439–454. https://doi.org/10.14214/ma.6232. [In Finnish with English summary].
Niemistö P. (2013). The monitoring of daily and annual growth and other changes in spruce, pine, and birch stem diameters with girth bands in Finland, 2009–2011. In: Merilä P., Jortikka S. (eds.). Forest Condition Monitoring in Finland – National report. The Finnish Forest Research Institute. p. 10.
Niemistö P., Hukki P., Verkasalo E. (1997). Kasvupaikan ja puuston tiheyden vaikutus rauduskoivun ulkoiseen laatuun 30-vuotiaissa istutuskoivikoissa. [Effect of site quality and stand density on quality of silver birch in 30-year-old planted stands]. Metsätieteen aikakauskirja – Folia Forestalia 3/1997: 349–374. https://doi.org/10.14214/ma.6476. [In Finnish with English summary].
O’Hara K.L. (2007). Pruning wounds and occlusion: a long-standing conundrum in forestry. Journal of Forestry 105(3): 131–138. https://doi.org/10.1093/jof/105.3.131.
O’Hara K.L., Kevin L., Buckland P.A. (1996). Prediction of pruning wound occlusion and defect core size in ponderosa pine. Western Journal of Applied Forestry 11(2): 40–43.
Oikarinen M. (1983). Etelä-Suomen viljeltyjen rauduskoivikoiden kasvatusmallit. [Growth and yield models for silver birch (Betula pendula) plantations in southern Finland]. Communicationes Instituti Forestalis Fenniae 113. 75 p. http://urn.fi/URN:ISBN:951-40-0619-4. [In Finnish with English summary].
Raulo J. (1977). Development of dominant trees in Betula pendula Roth and Betula pubescens Ehrh. plantations. Communicationes Instituti Forestalis Fenniae 90(4). 14 p. http://urn.fi/URN:NBN:fi-metla-201207171123.
Raulo J. (1979). Rauduskoivujälkeläistöjen rungon laatu Etelä- ja Keski-Suomessa. [Stem quality of Betula pendula Roth progenies in South and Central Finland]. Communicationes Instituti Forestalis Fenniae 97(5). 39 p. http://urn.fi/URN:NBN:fi-metla-201207171127. [In Finnish with English summary].
Raulo J., Saarnio R., Ylitalo T. (1978). Visakoivun karsittujen oksien kyljestyminen ja värivian leviäminen niistä runkoon. [Sealing-off of pruned branch stubs in curly birch and subsequent spread of discolouration into the stemwood]. Silva Fennica 12(4): 257–263. https://doi.org/10.14214/sf.a14864. [In Finnish with English summary].
R Core Team. (2018). R: a language and environment for statistical computing. R foundation for statistical computing. Vienna, Austria. https://www.R-project.org/. [Cited 17 Jan 2019].
Rintala P. (1995). Rauduskoivun pystykarsintavikojen yhteys karsittavien oksien kokoon ja laatuun sekä karsintavuodenaikaan. [Effect of pruning defects in silver birch on the size and quality of pruned branches and pruning season]. Metsäteknologian syventävien opintojen tutkielma. Joensuun yliopisto, metsätieteellinen tiedekunta. 105 p. [In Finnish].
Roth E.R. (1948). Healing and defects following oak pruning. Journal of Forestry 46(7): 500–504.
Schatz U., Heräjärvi H., Kannisto K., Rantatalo M. (2008). Influence of saw and secateur pruning on stem discolouration, wound cicatrisation and diameter growth of Betula pendula. Silva Fennica 42(2): 295–305. https://doi.org/10.14214/sf.258.
Sheppard J., Urmes M., Morhart C., Spiecker H. (2016). Factors affecting branch wound occlusion and associated decay following pruning – a case study with wild cherry (Prunus avium L.). Annals of Silvicultural Research 40(2): 133–139. http://dx.doi.org/10.12899/asr-1193.
Skovsgaard J.P., Ols C., Mc Carthy R. (2018). Highpruning of silver birch (Betula pendula Roth): work efficiency as a function of pruning method, pole saw type, slash removal, operator, pruning height and branch characteristics. International Journal of Forest Engineering 29(2): 117–127. https://doi.org/10.1080/14942119.2018.1462593.
Stener L.G., Jansson G. (2005). Improvement of Betula pendula by clonal and progeny testing of phenotypically selected trees. Scandinavian Journal of Forest Research 20(4): 292–303. https://doi.org/10.1080/02827580510036265.
Stener L.-G., Rytter L., Jansson G. (2017). Effects of pruning on wood properties of planted silver birch in southern Sweden. Silva Fennica 51(2) article 1713. https://doi.org/10.14214/sf.1713.
Vadla K. (1999). Finérutbytte og –kvalitet hos stammekvistet of ikke stammekvistet furu, bjørk of osp. [Veneer yield and quality of pruned and non-pruned spruce, birch, and aspen]. Norsk institutt for skogforskning, Rapport 13/1999. 21 p. + Appendices 3 p. [In Norwegian].
Valkonen S. (1992). Pellolle v. 1971 viljeltyjen raudus- ja hieskoivusekametsiköiden kehitys ja tuotos. [Development and yield of mixed silver and downy birch stands regenerated in 1971 on former agricultural land]. Metsäntuotantotieteen syventävien opintojen tutkielma. Joensuun yliopisto, metsätieteellinen tiedekunta. 41 p. [In Finnish].
Verkasalo E. (1997). Hieskoivun laatu vaneripuuna. [Quality of European white birch (Betula pubescens Ehrh.) for veneer and plywood.]. The Finnish Forest Research Institute, Research Papers 632. 483 p. + appendices 59 p. http://urn.fi/URN:ISBN:951-40-1555-X. [In Finnish].
Verkasalo E., Rintala P. (1998). Rauduskoivun pystykarsintavikojen riippuvuus oksien paksuudesta, laadusta ja karsinnan vuodenajasta. [Dependence of the defects in pruned silver birches on the size and quality of branches and on the pruning season]. Metsätieteen aikakauskirja – Folia Forestalia 2/1998: 151–178. https://doi.org/10.14214/ma.6960. [In Finnish with English summary].
Viherä-Aarnio A., Velling P. (1999). Growth and stem quality of mature birches in a combined species and progeny trial. Silva Fennica 33(3): 225–234. https://doi.org/10.14214/sf.659.
Vuokila Y. (1976). Karsimisen vaikutus männyn ja koivun terveydentilaan. [Effect of green pruning on the health of pine and birch]. Folia Forestalia 281. 13 p. http://urn.fi/URN:ISBN:951-40-0233-4. [In Finnish with English summary].
Walker S.H., Duncan D.B. (1967). Estimation of the probability of an event as a function of several independent variables. Biometrika 54(1): 167–178. https://doi.org/10.1093/biomet/54.1-2.167.
Wang C., Zhao Z., Hein S., Zeng J., Schuler J., Guo J., Guo W., Zeng J. (2015). Effect of planting density on knot attributes and branch occlusion of Betula alnoides under natural pruning in Southern China. Forests 6(4): 1343–1361. https://doi.org/10.3390/f6041343.
Wang C., Hein S., Zhao Z., Guo J., Zeng J. (2016). Branch occlusion and discoloration of Betula alnoides under artificial and natural pruning. Forest Ecology and Management 375: 200–210. https://doi.org/10.1016/j.foreco.2016.05.027.
Wang C., Zeng J., Hein S., Zhao Z., Guo J., Zeng J. (2017). Crown and branch attributes of mid-aged Betula alnoides plantations in response to planting density. Scandinavian Journal of Forest Research 32(8): 679–687. https://doi.org/10.1080/02827581.2016.1261936.
Wang C., Tang C., Hein S., Guo J., Zhao Z., Zeng J. (2018). Branch development of five-year-old Betula alnoides plantations in response to planting density. Forests 9(1): 42. https://doi.org/10.3390/f9010042.
Zar J.H. (1984). Biostatistical analysis. Second edition. Prentice-Hall, Inc., Englewood Cliffs, New Jersey. 718 p.
Total of 66 references.

